第二单元线与角复习(课件)- 四年级上册数学 北师大版(共19张PPT)
文档属性
| 名称 | 第二单元线与角复习(课件)- 四年级上册数学 北师大版(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-22 07:16:24 | ||
图片预览


文档简介
(共19张PPT)
线与角
线的认识
相交与垂直
平移与平行
旋转与角
角的度量(一)
角的度量(二)
线段、射线、直线
认识相交与垂直
认识平行线
这个单元我们学习了什么?
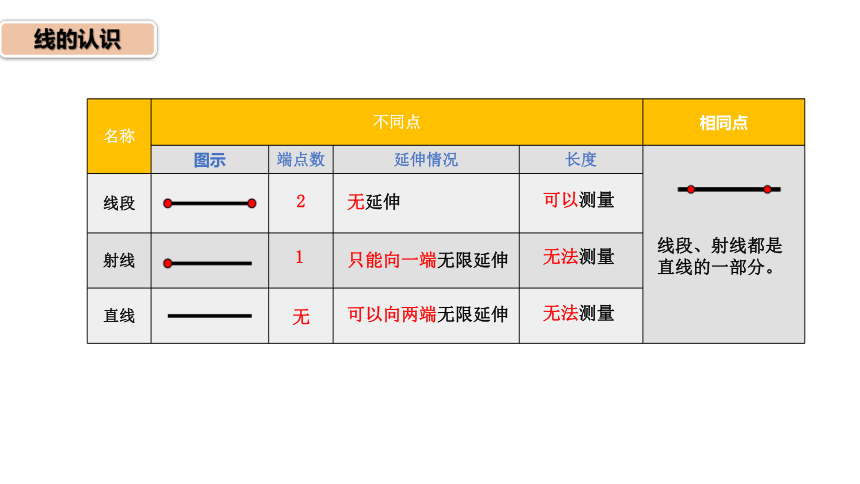
线的认识
名称 不同点 相同点
图示 端点数 延伸情况 长度
线段
射线
直线
2
1
无
无延伸
只能向一端无限延伸
可以向两端无限延伸
可以测量
无法测量
无法测量
线段、射线都是直线的一部分。
直线只有1条射线数=端点数×2线段数=基础线段的个数+……+1 直线数=1端点有4个,射线数=4×2=8基础线段有3段,线段数=3+2+1=6
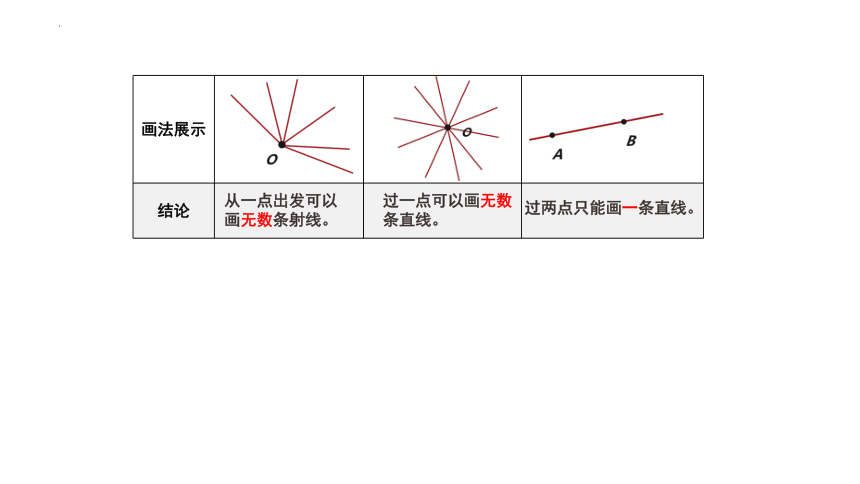
画法展示
结论
过一点可以画无数条直线。
从一点出发可以画无数条射线。
过两点只能画一条直线。
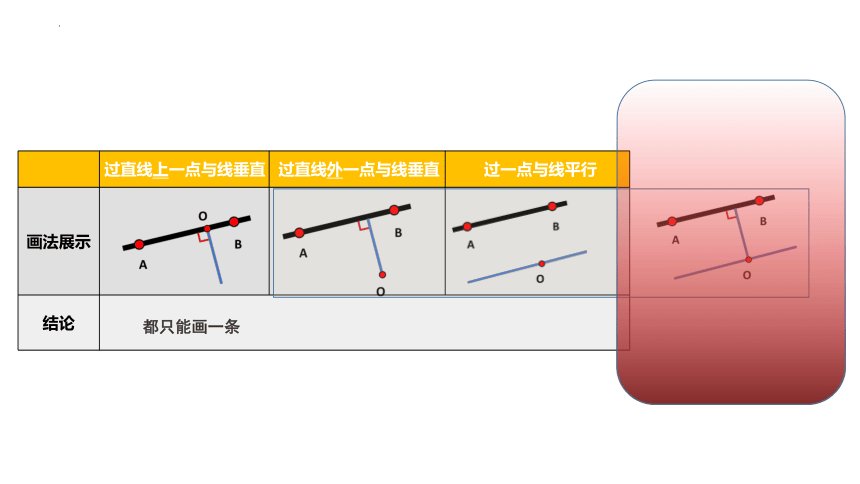
画法展示
结论
都只能画一条
过直线上一点与线垂直
过直线外一点与线垂直
过一点与线平行
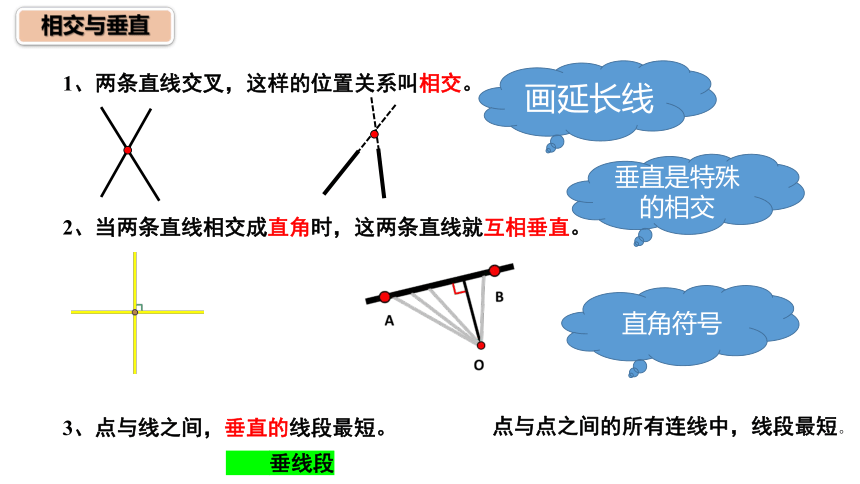
1、两条直线交叉,这样的位置关系叫相交。
2、当两条直线相交成直角时,这两条直线就互相垂直。
3、点与线之间,垂直的线段最短。
垂线段
相交与垂直
画延长线
点与点之间的所有连线中,线段最短。
垂直是特殊的相交
直角符号
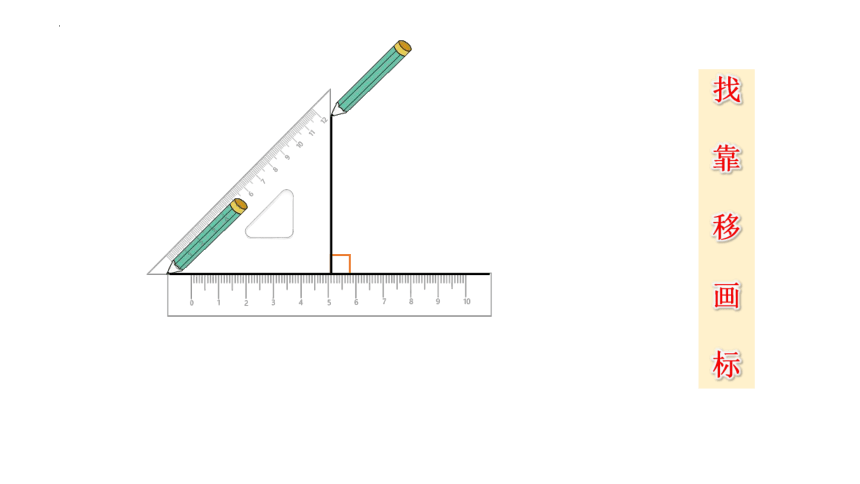
找
靠
移
画
标
1、在同一个平面内永不相交的两条直线叫作平行线,
也可以说这两条直线互相平行。
2、平行线的特点:
①平行线之间的距离处处相等。
②平行线永不相交。
3、两条互相平行的线段,与它们的长短无关。
平移与平行
用三角尺平移也能画出一组平行线。
定
靠
移
画
平移与平行
在同一平面内,两条直线都和另一条直线垂直,这两条直线互相平行。
比较得出:锐角<直角<钝角<平角<周角
锐角<90°
直角=90°
90°<钝角<180°
平角=180°
周角=360°
时钟的角
12:00 3:00
12:30 9:30
平角:是由一个顶点和两条射线组成的,这两条射线在同一直线上。
直线:是一条没有端点,可以无限延伸的线。
O
A
B
(B)
M
N
平角是一条直线吗?
旋转与角
周角:一条射线整整旋转了一周后与原来的射线重合。
射线:具有一个端点,只能向一边无限延伸。
O
(B)
A
M
N
周角是一条射线吗?
旋转与角
折纸
发现
1个平角 = 2个直角
1个周角 = 2个平角 = 4个直角
周角 平角 直角
旋转与角
一个平角与一个钝角的差,一定是锐角。
一个直角与锐角的和,一定是钝角。
1、将圆平均分成 360 份,其中的 1 份所对的角的大小叫作 1 度(记作1°)。
2、通常用 1°作为度量角的单位。
3、1周角=360°
1平角=180°
1直角=90°
角的度量(一)
中心点
零刻度线
外圈刻度
内圈刻度
量角器
点重合(顶点、中心点)
线重合(零刻度线、一条边)
0在内读内,0在外读外
量角的步骤
60°
画射线
对准点
线重合
点刻度
连射线
画角的步骤
标角度
135°
45°
45°
30°
60°
线与角
线的认识
相交与垂直
平移与平行
旋转与角
角的度量(一)
角的度量(二)
线段、射线、直线
认识相交与垂直
认识平行线
这个单元我们学习了什么?
线的认识
名称 不同点 相同点
图示 端点数 延伸情况 长度
线段
射线
直线
2
1
无
无延伸
只能向一端无限延伸
可以向两端无限延伸
可以测量
无法测量
无法测量
线段、射线都是直线的一部分。
直线只有1条射线数=端点数×2线段数=基础线段的个数+……+1 直线数=1端点有4个,射线数=4×2=8基础线段有3段,线段数=3+2+1=6
画法展示
结论
过一点可以画无数条直线。
从一点出发可以画无数条射线。
过两点只能画一条直线。
画法展示
结论
都只能画一条
过直线上一点与线垂直
过直线外一点与线垂直
过一点与线平行
1、两条直线交叉,这样的位置关系叫相交。
2、当两条直线相交成直角时,这两条直线就互相垂直。
3、点与线之间,垂直的线段最短。
垂线段
相交与垂直
画延长线
点与点之间的所有连线中,线段最短。
垂直是特殊的相交
直角符号
找
靠
移
画
标
1、在同一个平面内永不相交的两条直线叫作平行线,
也可以说这两条直线互相平行。
2、平行线的特点:
①平行线之间的距离处处相等。
②平行线永不相交。
3、两条互相平行的线段,与它们的长短无关。
平移与平行
用三角尺平移也能画出一组平行线。
定
靠
移
画
平移与平行
在同一平面内,两条直线都和另一条直线垂直,这两条直线互相平行。
比较得出:锐角<直角<钝角<平角<周角
锐角<90°
直角=90°
90°<钝角<180°
平角=180°
周角=360°
时钟的角
12:00 3:00
12:30 9:30
平角:是由一个顶点和两条射线组成的,这两条射线在同一直线上。
直线:是一条没有端点,可以无限延伸的线。
O
A
B
(B)
M
N
平角是一条直线吗?
旋转与角
周角:一条射线整整旋转了一周后与原来的射线重合。
射线:具有一个端点,只能向一边无限延伸。
O
(B)
A
M
N
周角是一条射线吗?
旋转与角
折纸
发现
1个平角 = 2个直角
1个周角 = 2个平角 = 4个直角
周角 平角 直角
旋转与角
一个平角与一个钝角的差,一定是锐角。
一个直角与锐角的和,一定是钝角。
1、将圆平均分成 360 份,其中的 1 份所对的角的大小叫作 1 度(记作1°)。
2、通常用 1°作为度量角的单位。
3、1周角=360°
1平角=180°
1直角=90°
角的度量(一)
中心点
零刻度线
外圈刻度
内圈刻度
量角器
点重合(顶点、中心点)
线重合(零刻度线、一条边)
0在内读内,0在外读外
量角的步骤
60°
画射线
对准点
线重合
点刻度
连射线
画角的步骤
标角度
135°
45°
45°
30°
60°
同课章节目录
- 一 认识更大的数
- 1 数一数
- 2 认识更大的数
- 3 人口普查
- 4 国土面积
- 5 近似数
- 6 从结绳计数说起
- 二 线与角
- 1 线的认识
- 2 相交与垂直
- 3 平移与平行
- 4 旋转与角
- 5 角的度量(一)
- 6 角的度量(二)
- 三 乘法
- 1 卫星运行时间
- 2 有多少名观众
- 3 神奇的计算工具
- 4 有趣的算式
- 四 运算律
- 1 买文具
- 2 加法交换律和乘法交换律
- 3 加法结合律
- 4 乘法结合律
- 5 乘法分配律
- 五 方向与位置
- 1 去图书馆
- 2 确定位置
- 六 除法
- 1 买文具
- 2 参观花圃
- 3 秋游
- 4 商不变的规律
- 5 路程、时间与速度
- 七 生活中的负数
- 1 温度
- 2 正负数
- 数学好玩
- 1 滴水试验
- 2 编码
- 3 数图形的学问
- 八 可能性
- 1 不确定性
- 2 摸球游戏
