6.3 实数(第二课时)课件
文档属性
| 名称 | 6.3 实数(第二课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 211.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-23 00:00:00 | ||
图片预览






文档简介
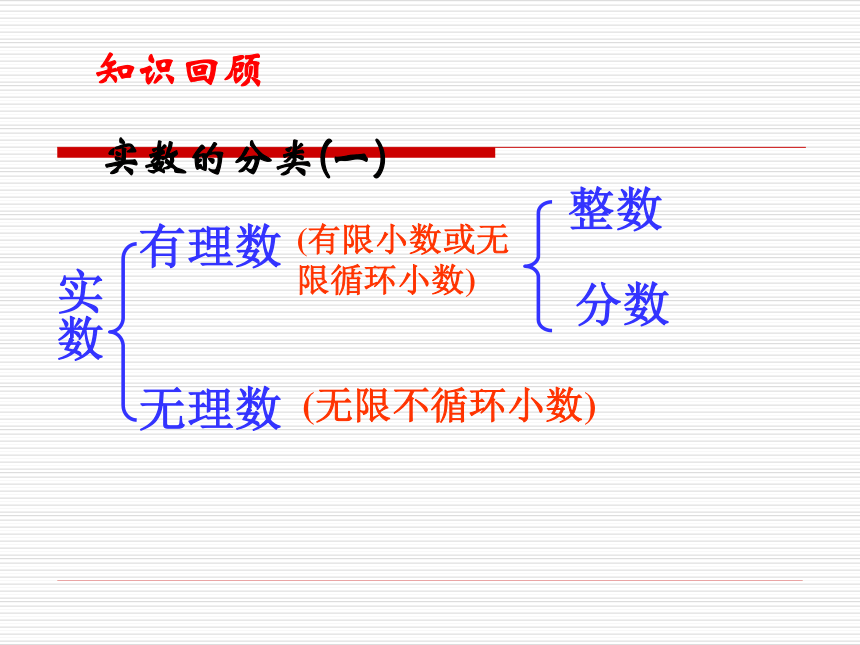
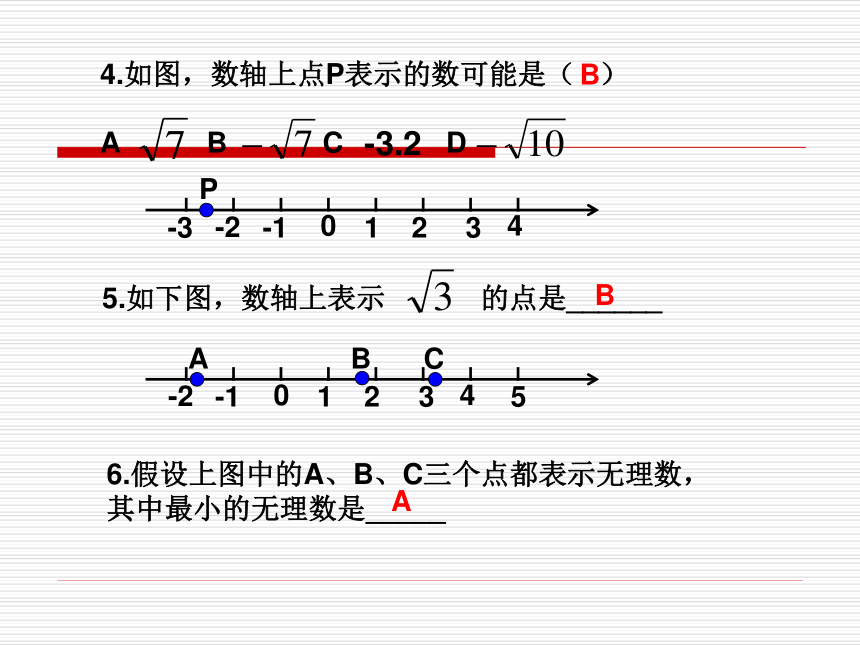
课件24张PPT。6.3 实数 第2课时实数的分类(一)实数有理数无理数整数分数(有限小数或无限循环小数)(无限不循环小数)知识回顾实数的分类(二)实数正实数负实数正有理数正无理数0负无理数负有理数判断下列说法是否正确:1.无理数都是无限不循环小数。( )2.两个无理数之积不一定是无理数。( )3.两个无理数之和一定是无理数。( )×有理数呢?复习巩固4.如图,数轴上点P表示的数可能是( )
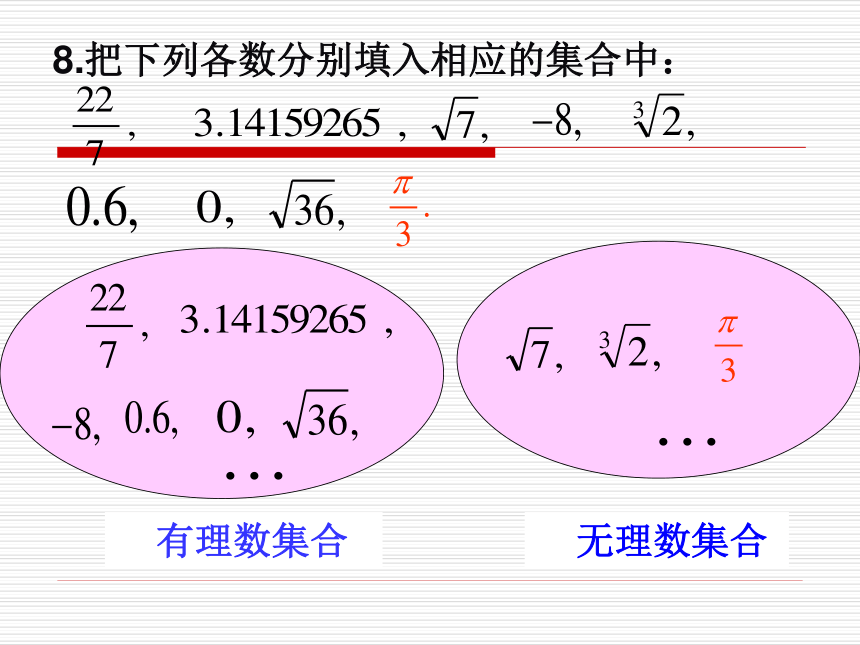
A B C D-3.25.如下图,数轴上表示 的点是______6.假设上图中的A、B、C三个点都表示无理数,其中最小的无理数是_____BBA7.判断下列说法是否正确:(2).所有的实数都可以用数轴上的点表示,反过来,数轴上所有的点都表示实数。( )×(1).所有的有理数都可以用数轴上的点表示,反过来,数轴上所有的点都表示有理数。( ) 有理数集合 无理数集合8.把下列各数分别填入相应的集合中:复习回顾(1)交换律 :加法 a+b=b+a
乘法a×b=b×a(2)结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)(3)分配律: a× (b+c)= a×b+ a×c1、有理数的运算律有哪些?知识回顾2、有理数的运算顺序是什么? 先算乘方,再算乘除,最后算加减。如果遇到括号, 则先进行括号里的运算 实数和有理数一样也可以进行加、减、乘、除(除数不为0)、乘方运算,而且正数及0可以进行开平方运算,任意一个实数可以进行开立方运算.在进行实数的运算时,有理数的运算法则与运算律对实数仍然适用。实数的运算法则 先算乘方和开方,再算乘除,最后算加减。如果遇到括号,则先进行括号里的运算.实数的运算顺序例如:乘法交换律乘法结合律分配律例1、计算下列各式的值:解:(分配律)(加法结合律)练习.计算解:2、计算:(3)(4)(2)(1)
3、计算下列各式的值:例2、计算:≈2.236+3.142≈5.38≈1.732×1.414≈2.45解:(1)无理数近似值多取1位;(2)结果按要求取近似值。注意:练习5、如图,A、B两点的坐标分别为
求△OAB的面积(精确到0.1)。-3 -2 -1 o 1 2 3 4 2
1
-1
-2
____≈1.6答:?OAB的面积约是1.6.课堂小结1. 实数的运算法则2. 实数的运算顺序3. 数轴上的点与实数的对应关系作业布置习题6.3 复习巩固 5
拓广探索 9
A B C D-3.25.如下图,数轴上表示 的点是______6.假设上图中的A、B、C三个点都表示无理数,其中最小的无理数是_____BBA7.判断下列说法是否正确:(2).所有的实数都可以用数轴上的点表示,反过来,数轴上所有的点都表示实数。( )×(1).所有的有理数都可以用数轴上的点表示,反过来,数轴上所有的点都表示有理数。( ) 有理数集合 无理数集合8.把下列各数分别填入相应的集合中:复习回顾(1)交换律 :加法 a+b=b+a
乘法a×b=b×a(2)结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)(3)分配律: a× (b+c)= a×b+ a×c1、有理数的运算律有哪些?知识回顾2、有理数的运算顺序是什么? 先算乘方,再算乘除,最后算加减。如果遇到括号, 则先进行括号里的运算 实数和有理数一样也可以进行加、减、乘、除(除数不为0)、乘方运算,而且正数及0可以进行开平方运算,任意一个实数可以进行开立方运算.在进行实数的运算时,有理数的运算法则与运算律对实数仍然适用。实数的运算法则 先算乘方和开方,再算乘除,最后算加减。如果遇到括号,则先进行括号里的运算.实数的运算顺序例如:乘法交换律乘法结合律分配律例1、计算下列各式的值:解:(分配律)(加法结合律)练习.计算解:2、计算:(3)(4)(2)(1)
3、计算下列各式的值:例2、计算:≈2.236+3.142≈5.38≈1.732×1.414≈2.45解:(1)无理数近似值多取1位;(2)结果按要求取近似值。注意:练习5、如图,A、B两点的坐标分别为
求△OAB的面积(精确到0.1)。-3 -2 -1 o 1 2 3 4 2
1
-1
-2
____≈1.6答:?OAB的面积约是1.6.课堂小结1. 实数的运算法则2. 实数的运算顺序3. 数轴上的点与实数的对应关系作业布置习题6.3 复习巩固 5
拓广探索 9
