【新课标】1.5二次函数的应用 课件(共33张PPT)
文档属性
| 名称 | 【新课标】1.5二次函数的应用 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 10:02:50 | ||
图片预览










文档简介
(共33张PPT)
1.5二次函数的应用
湘教版 九年级下
教学内容分析
前几节学会了求二次函数y=ax2+bx+c的最值,在此基础上,对于实际问题,寻找问题中的数量关系,并会应用函数关系式求函数的最值。本节内容主要是运用二次函数的性质来解决实际问题.
教学目标
1.会求二次函数y=ax2+bx+c的最小(大)值(重点)
2.掌握实际问题中的数量关系,并会应用函数关系式求实际问题的最值(难点)
3.掌握二次函数的性质来解决实际问题.
核心素养分析
本节是在实际问题中寻找数量关系,建立二次函数模型,并会应用函数关系式的性质求实际问题,培养了学生建立数学模型的观念,同时也锻炼了学生运用模型解决实际问题的能力。
新知导入
二次函数y=ax +bx+c,
1、顶点坐标是什么?
2、当x等于多少,可以求最值呢?
答:1、顶点坐标为
2、当x等于顶点的横坐标时,达到最大值(当a<0)或最小值(当a>0),这个最大(小)值等于顶点的纵坐标.
新知讲解
如图1-18,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9m,当水面宽4m时,拱顶离水面2m. 若想了解水面宽度变化时,拱顶离水面高度怎样变化,你能建立函数模型来解决这个问题吗?
动脑筋
图1-18
新知讲解
拱桥的纵截面是抛物线的一部分,应当是某个二次函数的图象, 因此可以建立二次函数模型来刻画.
为简便起见,以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系
先建立直角坐标系
新知讲解
由于顶点坐标是(0,0),
因此这条抛物线的形式为y=ax2.
再设二次函数解析式
图1-19
新知讲解
已知水面宽4m时,拱顶离水面高2m,
因此点A(2,-2)在抛物线上.
由此得出-2=a·22,
解得
然后根据条件求出解析式
图1-19
新知讲解
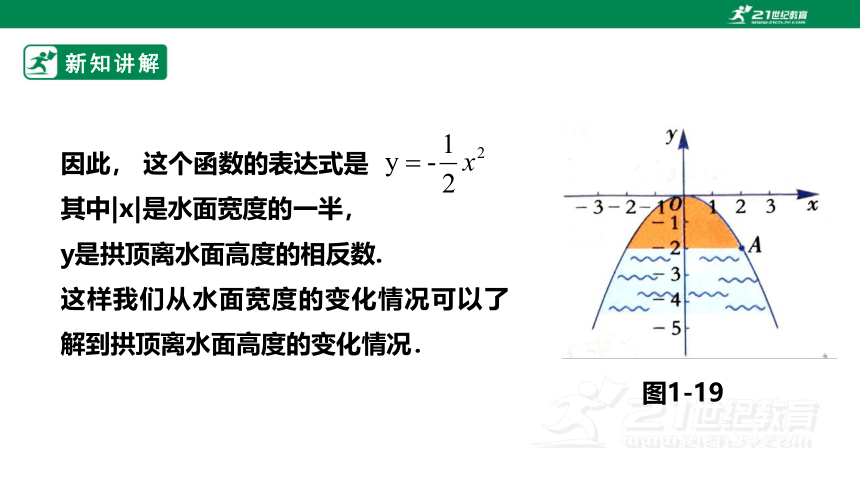
因此, 这个函数的表达式是
其中|x|是水面宽度的一半,
y是拱顶离水面高度的相反数.
这样我们从水面宽度的变化情况可以了解到拱顶离水面高度的变化情况.
图1-19
新知讲解
由于拱桥的跨度为4.9m,因此自变量x的取值范围是: -2.45≤x≤2.45.
想一想, 当水面宽 4.6m时, 拱顶离水面几米?
新知讲解
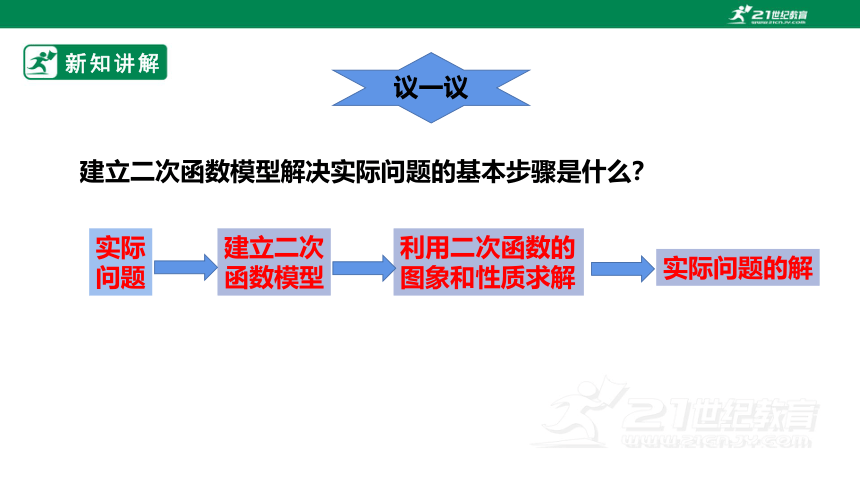
建立二次函数模型解决实际问题的基本步骤是什么?
议一议
实际
问题
建立二次
函数模型
利用二次函数的图象和性质求解
实际问题的解
新知讲解
解决二次函数应用题方法:
(1)根据题意建立二次函数模型,建立平面直角坐标系,以使解决问题简便为原则;
(2)求出抛物线的解析式(写出自变量的取值范围);
(3)根据二次函数的图象和性质解决问题;
(4)通过验证得出实际问题的答案.
新知讲解
如图1-20,用8m长的铝材做一个日字形窗框.试问:窗框的宽和高各为多少时,窗框的透光面积S(m2)最大 最大面积是多少
(假设铝材的宽度不计)
动脑筋
图1-20
新知讲解
由于做窗框的铝材长度已确定,而窗框的面积S随矩形一边长的变化而变化.
因此设窗框的宽为xm,则窗框的高为 m,其中 . 则窗框的透光面积为
将上式配方
新知讲解
当 时,S取最大值 ,这时高为2m.
则当窗框的宽为 ,高为2m时,窗框的透光面积最大,
最大透光面积为 m2 .
要考虑 是不是在x的取值范围内。
解二次函数应用题步骤:
1、审(题)
2、设(未知数)
3、列(函数)
4、解(最值)
5、(检)验
6、(解)答
新知讲解
新知讲解
例 某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元销售,那么一个月内可售出180件。根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件.当销售单价为多少元时,该店能在一个月内获得最大利润?
按照数量关系,总利润=单件利润×销售数量,建立函数模型解答.
新知讲解
解:设每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元。
则每月减少的销售量为10x件,
实际销售量为(180-10x)件。
单件利润为(30+x-20)元。
则y=(10+x)(180-10x),
新知讲解
即y=-10x2+80x+1800(0≤x≤18) .
将上式进行配方,
y=-10x2+80x+1800
=-10(x-4)2+1960.
当x=4时,即销售单价为34元时,y取最大值1960.
答:当销售单价定为34元时,该店在一个月内能获得最大利润1960元.
1、解应用题的步骤:
审、设、列、解、验、答
2、建立二次函数模型解决实际问题的基本步骤是
建立二次函数模型,利用二次函数的图象和性质求实际问题的解。
新知讲解
课堂练习
1.如图,一边靠学校院墙,其他三边用40米长的篱笆围成一个矩形花圃,设矩形ABCD的边AB=x米,面积为S平方米,则下面关系式正确的是( )
A. S=x(40-x) B. S=x(40-2x)
C. S=x(10-x) D. S=10(2x-20)
B
课堂练习
解:∵AB=x米,
∴BC=(40-2x)米,
∴S=x(40-2x).
故选:B.
课堂练习
2.一件工艺品进价为100元,标价135元售出,每天可售出100件.根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价 ( )
A. 5元 B. 10元 C. 15元 D. 20元
A
课堂练习
解:设每件需降价x元,每天获利y元,
则y=(135-x-100)(100+4x)
即:y=-4(x-5) 2+3600
∵-4<0,开口向下,
∴当x=5元时,每天获得的利润最大.
故选A.
课堂练习
3.如图,一抛物线型拱桥,当拱顶到水面的距离为2m时,水面宽度为4m,那么水位下降1m时,水面的宽度为( ) m.
A. B. 8 C. 5 D. 6
课堂练习
解:建立如图所示直角坐标系:
可设这条抛物线为y=ax2,
把点(2,-2)代入,得-2=a×22,
解得:
∴
课堂练习
当y=-3时,
解得:x=
∴水面下降1m,水面宽度为 m.
故选:A.
课堂总结
1、解应用题的步骤:
审、设、列、解、验、答
2、建立二次函数模型解决实际问题的基本步骤是
建立二次函数模型,利用二次函数的图象和性质求实际问题的解。
板书设计
1.5 二次函数的应用
1.求二次函数y=ax +bx+c最值
2.建立二次函数模型解决实际问题的基本步骤
作业布置
必做题:课本第32页练习的1,2,3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5二次函数的应用
湘教版 九年级下
教学内容分析
前几节学会了求二次函数y=ax2+bx+c的最值,在此基础上,对于实际问题,寻找问题中的数量关系,并会应用函数关系式求函数的最值。本节内容主要是运用二次函数的性质来解决实际问题.
教学目标
1.会求二次函数y=ax2+bx+c的最小(大)值(重点)
2.掌握实际问题中的数量关系,并会应用函数关系式求实际问题的最值(难点)
3.掌握二次函数的性质来解决实际问题.
核心素养分析
本节是在实际问题中寻找数量关系,建立二次函数模型,并会应用函数关系式的性质求实际问题,培养了学生建立数学模型的观念,同时也锻炼了学生运用模型解决实际问题的能力。
新知导入
二次函数y=ax +bx+c,
1、顶点坐标是什么?
2、当x等于多少,可以求最值呢?
答:1、顶点坐标为
2、当x等于顶点的横坐标时,达到最大值(当a<0)或最小值(当a>0),这个最大(小)值等于顶点的纵坐标.
新知讲解
如图1-18,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9m,当水面宽4m时,拱顶离水面2m. 若想了解水面宽度变化时,拱顶离水面高度怎样变化,你能建立函数模型来解决这个问题吗?
动脑筋
图1-18
新知讲解
拱桥的纵截面是抛物线的一部分,应当是某个二次函数的图象, 因此可以建立二次函数模型来刻画.
为简便起见,以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系
先建立直角坐标系
新知讲解
由于顶点坐标是(0,0),
因此这条抛物线的形式为y=ax2.
再设二次函数解析式
图1-19
新知讲解
已知水面宽4m时,拱顶离水面高2m,
因此点A(2,-2)在抛物线上.
由此得出-2=a·22,
解得
然后根据条件求出解析式
图1-19
新知讲解
因此, 这个函数的表达式是
其中|x|是水面宽度的一半,
y是拱顶离水面高度的相反数.
这样我们从水面宽度的变化情况可以了解到拱顶离水面高度的变化情况.
图1-19
新知讲解
由于拱桥的跨度为4.9m,因此自变量x的取值范围是: -2.45≤x≤2.45.
想一想, 当水面宽 4.6m时, 拱顶离水面几米?
新知讲解
建立二次函数模型解决实际问题的基本步骤是什么?
议一议
实际
问题
建立二次
函数模型
利用二次函数的图象和性质求解
实际问题的解
新知讲解
解决二次函数应用题方法:
(1)根据题意建立二次函数模型,建立平面直角坐标系,以使解决问题简便为原则;
(2)求出抛物线的解析式(写出自变量的取值范围);
(3)根据二次函数的图象和性质解决问题;
(4)通过验证得出实际问题的答案.
新知讲解
如图1-20,用8m长的铝材做一个日字形窗框.试问:窗框的宽和高各为多少时,窗框的透光面积S(m2)最大 最大面积是多少
(假设铝材的宽度不计)
动脑筋
图1-20
新知讲解
由于做窗框的铝材长度已确定,而窗框的面积S随矩形一边长的变化而变化.
因此设窗框的宽为xm,则窗框的高为 m,其中 . 则窗框的透光面积为
将上式配方
新知讲解
当 时,S取最大值 ,这时高为2m.
则当窗框的宽为 ,高为2m时,窗框的透光面积最大,
最大透光面积为 m2 .
要考虑 是不是在x的取值范围内。
解二次函数应用题步骤:
1、审(题)
2、设(未知数)
3、列(函数)
4、解(最值)
5、(检)验
6、(解)答
新知讲解
新知讲解
例 某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元销售,那么一个月内可售出180件。根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件.当销售单价为多少元时,该店能在一个月内获得最大利润?
按照数量关系,总利润=单件利润×销售数量,建立函数模型解答.
新知讲解
解:设每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元。
则每月减少的销售量为10x件,
实际销售量为(180-10x)件。
单件利润为(30+x-20)元。
则y=(10+x)(180-10x),
新知讲解
即y=-10x2+80x+1800(0≤x≤18) .
将上式进行配方,
y=-10x2+80x+1800
=-10(x-4)2+1960.
当x=4时,即销售单价为34元时,y取最大值1960.
答:当销售单价定为34元时,该店在一个月内能获得最大利润1960元.
1、解应用题的步骤:
审、设、列、解、验、答
2、建立二次函数模型解决实际问题的基本步骤是
建立二次函数模型,利用二次函数的图象和性质求实际问题的解。
新知讲解
课堂练习
1.如图,一边靠学校院墙,其他三边用40米长的篱笆围成一个矩形花圃,设矩形ABCD的边AB=x米,面积为S平方米,则下面关系式正确的是( )
A. S=x(40-x) B. S=x(40-2x)
C. S=x(10-x) D. S=10(2x-20)
B
课堂练习
解:∵AB=x米,
∴BC=(40-2x)米,
∴S=x(40-2x).
故选:B.
课堂练习
2.一件工艺品进价为100元,标价135元售出,每天可售出100件.根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价 ( )
A. 5元 B. 10元 C. 15元 D. 20元
A
课堂练习
解:设每件需降价x元,每天获利y元,
则y=(135-x-100)(100+4x)
即:y=-4(x-5) 2+3600
∵-4<0,开口向下,
∴当x=5元时,每天获得的利润最大.
故选A.
课堂练习
3.如图,一抛物线型拱桥,当拱顶到水面的距离为2m时,水面宽度为4m,那么水位下降1m时,水面的宽度为( ) m.
A. B. 8 C. 5 D. 6
课堂练习
解:建立如图所示直角坐标系:
可设这条抛物线为y=ax2,
把点(2,-2)代入,得-2=a×22,
解得:
∴
课堂练习
当y=-3时,
解得:x=
∴水面下降1m,水面宽度为 m.
故选:A.
课堂总结
1、解应用题的步骤:
审、设、列、解、验、答
2、建立二次函数模型解决实际问题的基本步骤是
建立二次函数模型,利用二次函数的图象和性质求实际问题的解。
板书设计
1.5 二次函数的应用
1.求二次函数y=ax +bx+c最值
2.建立二次函数模型解决实际问题的基本步骤
作业布置
必做题:课本第32页练习的1,2,3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
