【原创精品】人教版数学九年级下册 26.3.1 《反比例函数章末复习》课件 (共29张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 26.3.1 《反比例函数章末复习》课件 (共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览







文档简介
(共29张PPT)
26.3.1 章末复习
人教版九年级下册
第二十六章 反比例函数
1.掌握5个考点内容.
2.熟悉5个题型.
3.熟记5答题方法.
重点:掌握5个考点内容.
难点:熟悉5个题型及跟踪训练题.
学习目标
重点难点
考点1 反比例函数的的概念
考点2 反比例函数的图象
考点3 反比例函数的性质
考点4 反比例函数中比例系数k的几何意义
考点5 反比例函数的应用
反比例函数
考点1 反比例函数的的概念
一般地,如果两个变量x、y之间的关系可以表示成y=k/x(k为常数,k≠0)的形式,那么称y是x的反比例函数.
反比例函数自变量不能为0
D
判断是否反比例函数,要根据反比例函数表达式判断,不能忽视比例系数不为0的条件.
如何判断是否为按比例函数的方法
变式训练
A
考点2 反比例函数的图象
画法:列表、描点、连续
形状:双曲线(与坐标无交点)
是中心对称图形,对称中心:坐标原点.
是轴对称图形,对称轴是y=±x.
位置:当k>0,图象位于第一、三象限内;当k<0,图象位于第二、四象限内.
A
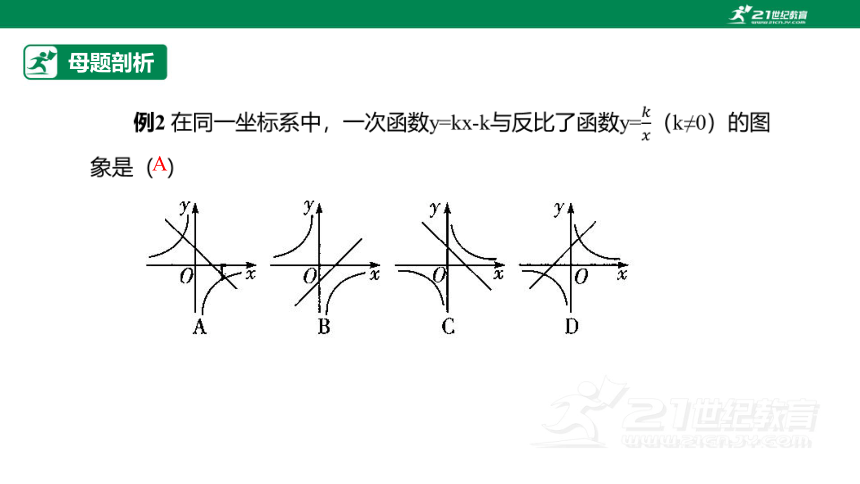
先从两个函数图象中选择一个判断k的符号,再根据k的符号判断另一个函数图象的正确性,采取一一判断排除法.
判断K值的方法
A
考点3 反比例函数的性质
当k>0,在每个象限内y随x的增大而增大;
当k<0,在每个象限内y随x的增大而减小.
D
运用反比例函数的性质,一定要扣做同一象限,不在同一象限,分象限确定正负,同一象限利用增减性比较大小.
运用反比例函数的方法
D
考点4 反比例函数中比例系数k的几何意义.
k的绝对值等于反比例函数图象上任意一点向两坐标轴作垂线段与坐标轴围成的矩形的面积.
-6
解反比例函数图象与几何图形的面积问题一般分为两类:一类是根据面积求反比例函数表达式,另-类是由已知的表达式求几何图形的面积.而求面积时,有时可利用反比例函数比例系数k的绝对值,有时则需利用几个几何图形面积的和差来求得.
反比例函数求几何面积的方法
下列图形中,阴影部分面积最大的是( )
C
考点5 反比例函数的应用
例5 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(小时)之间的函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数表达式;
(2)血液中药物浓度不低于4微克/毫升的持续时间多少小时?
解:(1)当0≤x≤4时,设直线解析式为:y=kx(k≠0),
将(4,8)代入得:8=4k,解得:k=2,
故直线解析式为:y=2x.
当4≤x≤10时,设反比例函数解析式为:y=a/x (a≠0),
将(4,8)代入得:8= a/4 ,解得:a=32,
故反比例函数的解析式为:y= 32/x (4≤x≤10),
因此血液中药物浓度上升阶段的函数关系式为y=2x(0≤x≤4),
下降阶段的函数关系式为y= 32/x (4≤x≤10).
考点5 反比例函数的应用
例5 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(小时)之间的函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数表达式;
(2)血液中药物浓度不低于4微克/毫升的持续时间多少小时?
解:(2)血液中药物浓度不低于4微克/毫升
即y≥4时,令4=2x,
解得:x=2.
令4= 32/x ,
解得:x=8,
∵8-2=6(小时),
∴血液中药物浓度不低于4微克/毫升的持续时间为6小时.
解决反比例函数与一次函数综合的应用题时,求函数表达式要把握分界点;在求函数值对应的自变量值时,注意代入两个函数关系式求解.
比较反比例函数值的大小一般有三种方法
用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系。寄宿生小红、小敏晚饭后用同一种洗衣粉各自洗一件同样的衣服,漂洗时,小红每次用一盆水(约10升),小敏每次用半盆水(约5升),如果她们都用了5克洗衣粉,第一次漂洗后,小红的衣服中残留的洗衣粉还有1.5克,小敏的衣服中残留的洗衣粉还有2克。
(1)请帮助小红、小敏求出各自衣服中洗衣粉的残留量y与漂洗次数x的函数关系式。
病人按规定的剂量服用某种药物,测得服药后 2 小时,每毫升血液中的含药量达到最大值为 4 毫克. 已知服药后,2 小时前每毫升血液中的含药量 y (单位:毫克)与时间 x (单位:小时) 成正比例;2 小时后 y 与 x 成反比例 (如图). 根据以上信息解答下列问题:
(1) 求当 0 ≤ x ≤2 时,y 与 x 的函数解析式;
解:当 0 ≤ x ≤2 时,y 与 x 成正比例函数关系.
设 y =kx,由于点 (2,4) 在线段上,
所以 4=2k,k=2,即 y=2x.
O
y/毫克
x/小时
2
4
(2) 求当 x > 2 时,y 与 x 的函数解析式;
解:当 x > 2时,y 与 x 成反比例函数关系,
设
解得 k =8.
由于点 (2,4) 在反比例函数的图象上,
所以
即
O
y/毫克
x/小时
2
4
(3) 若每毫升血液中的含药量不低于 2 毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
解:当 0≤x≤2 时,含药量不低于 2 毫克,即 2x≥2,
解得x≥1,∴1≤x≤2;
当 x>2 时,含药量不低于 2 毫克,
即 ≥ 2,解得 x ≤ 4. ∴2< x ≤4.
所以服药一次,治疗疾病的有
效时间是 1+2=3 (小时).
O
y/毫克
x/小时
2
4
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
26.3.1 章末复习
人教版九年级下册
第二十六章 反比例函数
1.掌握5个考点内容.
2.熟悉5个题型.
3.熟记5答题方法.
重点:掌握5个考点内容.
难点:熟悉5个题型及跟踪训练题.
学习目标
重点难点
考点1 反比例函数的的概念
考点2 反比例函数的图象
考点3 反比例函数的性质
考点4 反比例函数中比例系数k的几何意义
考点5 反比例函数的应用
反比例函数
考点1 反比例函数的的概念
一般地,如果两个变量x、y之间的关系可以表示成y=k/x(k为常数,k≠0)的形式,那么称y是x的反比例函数.
反比例函数自变量不能为0
D
判断是否反比例函数,要根据反比例函数表达式判断,不能忽视比例系数不为0的条件.
如何判断是否为按比例函数的方法
变式训练
A
考点2 反比例函数的图象
画法:列表、描点、连续
形状:双曲线(与坐标无交点)
是中心对称图形,对称中心:坐标原点.
是轴对称图形,对称轴是y=±x.
位置:当k>0,图象位于第一、三象限内;当k<0,图象位于第二、四象限内.
A
先从两个函数图象中选择一个判断k的符号,再根据k的符号判断另一个函数图象的正确性,采取一一判断排除法.
判断K值的方法
A
考点3 反比例函数的性质
当k>0,在每个象限内y随x的增大而增大;
当k<0,在每个象限内y随x的增大而减小.
D
运用反比例函数的性质,一定要扣做同一象限,不在同一象限,分象限确定正负,同一象限利用增减性比较大小.
运用反比例函数的方法
D
考点4 反比例函数中比例系数k的几何意义.
k的绝对值等于反比例函数图象上任意一点向两坐标轴作垂线段与坐标轴围成的矩形的面积.
-6
解反比例函数图象与几何图形的面积问题一般分为两类:一类是根据面积求反比例函数表达式,另-类是由已知的表达式求几何图形的面积.而求面积时,有时可利用反比例函数比例系数k的绝对值,有时则需利用几个几何图形面积的和差来求得.
反比例函数求几何面积的方法
下列图形中,阴影部分面积最大的是( )
C
考点5 反比例函数的应用
例5 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(小时)之间的函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数表达式;
(2)血液中药物浓度不低于4微克/毫升的持续时间多少小时?
解:(1)当0≤x≤4时,设直线解析式为:y=kx(k≠0),
将(4,8)代入得:8=4k,解得:k=2,
故直线解析式为:y=2x.
当4≤x≤10时,设反比例函数解析式为:y=a/x (a≠0),
将(4,8)代入得:8= a/4 ,解得:a=32,
故反比例函数的解析式为:y= 32/x (4≤x≤10),
因此血液中药物浓度上升阶段的函数关系式为y=2x(0≤x≤4),
下降阶段的函数关系式为y= 32/x (4≤x≤10).
考点5 反比例函数的应用
例5 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(小时)之间的函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数表达式;
(2)血液中药物浓度不低于4微克/毫升的持续时间多少小时?
解:(2)血液中药物浓度不低于4微克/毫升
即y≥4时,令4=2x,
解得:x=2.
令4= 32/x ,
解得:x=8,
∵8-2=6(小时),
∴血液中药物浓度不低于4微克/毫升的持续时间为6小时.
解决反比例函数与一次函数综合的应用题时,求函数表达式要把握分界点;在求函数值对应的自变量值时,注意代入两个函数关系式求解.
比较反比例函数值的大小一般有三种方法
用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系。寄宿生小红、小敏晚饭后用同一种洗衣粉各自洗一件同样的衣服,漂洗时,小红每次用一盆水(约10升),小敏每次用半盆水(约5升),如果她们都用了5克洗衣粉,第一次漂洗后,小红的衣服中残留的洗衣粉还有1.5克,小敏的衣服中残留的洗衣粉还有2克。
(1)请帮助小红、小敏求出各自衣服中洗衣粉的残留量y与漂洗次数x的函数关系式。
病人按规定的剂量服用某种药物,测得服药后 2 小时,每毫升血液中的含药量达到最大值为 4 毫克. 已知服药后,2 小时前每毫升血液中的含药量 y (单位:毫克)与时间 x (单位:小时) 成正比例;2 小时后 y 与 x 成反比例 (如图). 根据以上信息解答下列问题:
(1) 求当 0 ≤ x ≤2 时,y 与 x 的函数解析式;
解:当 0 ≤ x ≤2 时,y 与 x 成正比例函数关系.
设 y =kx,由于点 (2,4) 在线段上,
所以 4=2k,k=2,即 y=2x.
O
y/毫克
x/小时
2
4
(2) 求当 x > 2 时,y 与 x 的函数解析式;
解:当 x > 2时,y 与 x 成反比例函数关系,
设
解得 k =8.
由于点 (2,4) 在反比例函数的图象上,
所以
即
O
y/毫克
x/小时
2
4
(3) 若每毫升血液中的含药量不低于 2 毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
解:当 0≤x≤2 时,含药量不低于 2 毫克,即 2x≥2,
解得x≥1,∴1≤x≤2;
当 x>2 时,含药量不低于 2 毫克,
即 ≥ 2,解得 x ≤ 4. ∴2< x ≤4.
所以服药一次,治疗疾病的有
效时间是 1+2=3 (小时).
O
y/毫克
x/小时
2
4
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
