【原创精品】人教版数学九年级下册 27.1《图形的相似》课件 (共22张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 27.1《图形的相似》课件 (共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览






文档简介
(共22张PPT)
27.1.1 图形的相似
人教版九年级下册
第二十七章 相似
1、经历相似图形概念的形成过程,了解相似图形的含义。
2、进一步发展自己归纳、类比、反思、交流等方面的能力。
3、在解决问题过程中体会学习数学的乐趣,在独立思考的基础上,敢于发表自己的观点并尊重他人的见解。
重点:理解邻补角和对顶角的概念.
难点:探索相交线对顶角之间的关系.
学习目标
重点难点
我们刚才所见到的图形有什么相同点和不同点
相同点:
不同点:
形状相同.
大小不一定相同.
生活中我们会碰到许多这样形状相同的.大小不一定相同的图形,
在数学上,我们把具有相同形状的图形称为:相似图形
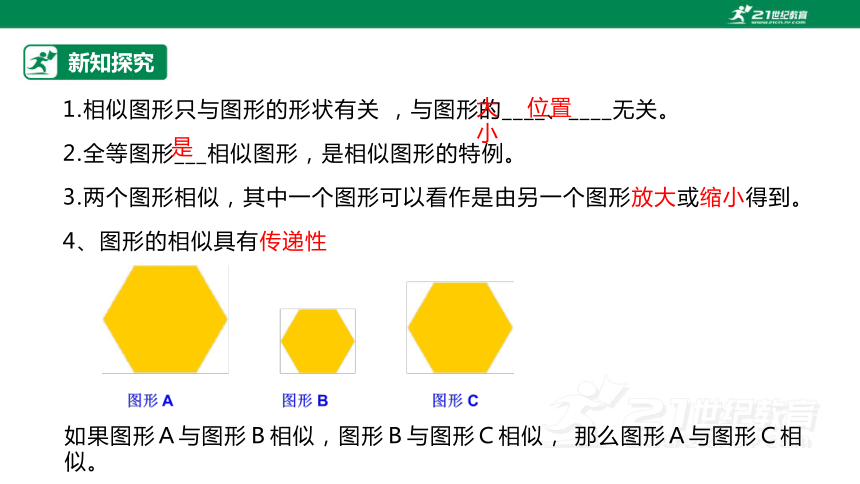
1.相似图形只与图形的形状有关 ,与图形的____、____无关。
2.全等图形___相似图形,是相似图形的特例。
3.两个图形相似,其中一个图形可以看作是由另一个图形放大或缩小得到。
4、图形的相似具有传递性
大小
位置
是
如果图形A与图形B相似,图形B与图形C相似, 那么图形A与图形C相似。
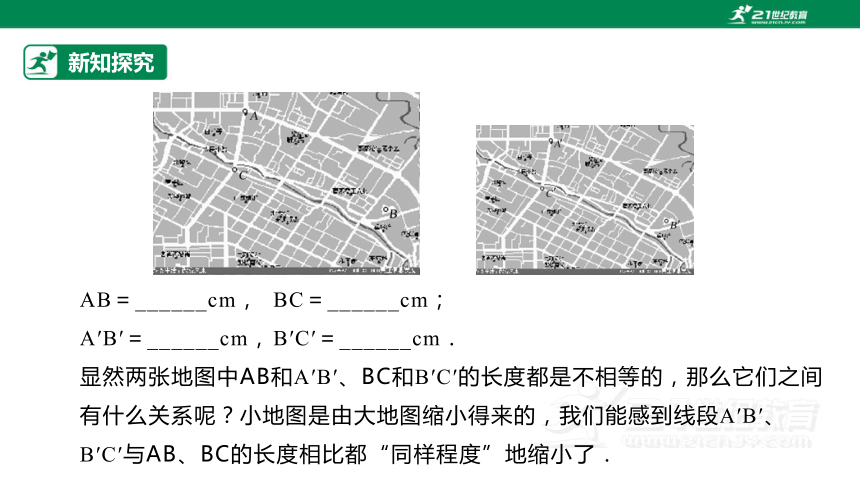
如图是某个城市的大小不同的两张地图,当然,它们是相似的图形.设在大地图中有A、B、C三地,在小地图中的相应三地记为A′、B′、C′,试用刻度尺量一量两张地图中A(A′)与B(B′)两地之间的图上距离、B(B′)与C(C′)两地之间的图上距离.
AB=______cm, BC=______cm;
A′B′=______cm, B′C′=______cm.
显然两张地图中AB和A′B′、BC和B′C′的长度都是不相等的,那么它们之间有什么关系呢?小地图是由大地图缩小得来的,我们能感到线段A′B′、B′C′与AB、BC的长度相比都“同样程度”地缩小了.
=____,
=____.
也就是说上面地图中AB、A′B′、BC、B′C′这四条线段是成比例线段.
想一想:线段AC与A′C′的比是否也等于AB与A′B′的比呢?
实际上,上面两张相似的地图中的对应线段都是成比例的.
猜想: ____ ____ ____ ____ ____。
思考:这样的结论对一般的相似多边形是否成立呢?
=
我们能发现:
想一想:
如果在这两张地图中
AB:A`B`≠BC:B`C`,那么会出现什么情况?
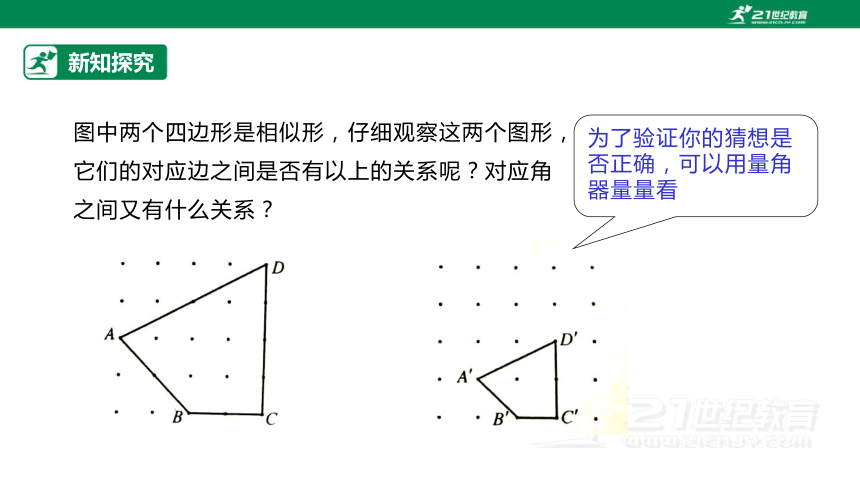
图中两个四边形是相似形,仔细观察这两个图形,它们的对应边之间是否有以上的关系呢?对应角之间又有什么关系?
为了验证你的猜想是否正确,可以用量角器量量看
相似多边形的性质:
相似多边形对应边成比例,对应角相等.
剖析:
(1)两个多边形的边数不同一定不是相似多边形;
(2)定义中“角对应相等”、“边对应成比例”是判定两个多边形是否相似的必备的条件,缺一不可。
两个三角形一定是相似图形吗?两个等腰三角形呢?两个等边三角形呢?
两个三角形不一定是相似图形
两个等腰三角形不一定是相似图形
两个等边三角形一定是相似图形
例、在图所示的相似四边形中,求未知边x的长度和角α的大小.
解: ∵ 两个四边形相似,
∴ 18:12=X:18;
∴ 12X=18×18;
即 X=27。
根据对应角相等,可得:
α =360 °-(77 °+83 °+116 °)=84 °
E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1,求矩形ABCD的面积。
1.制作一块3mX2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
C
2.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边为( )
A.3cm B.4cm C.4.5cm D.5cm
C
A
A
3.相似多边形对应边之比叫做___________.
4.两个相似多边形的最长边分别为10cm和20cm,其中一个多边形的最短边为5cm,则另一个多边形的最短边为 .
相似比
5. 梯形ABCD中,AD∥BC,E,F分别为AB,CD上一点,且梯形AEFD∽梯形EBCF,若AD=4,BC=9。试求AE:EB的值。
相似图形
形状相同的图形叫做相似图形
相似图形的大小不一定相同
相似多边形对应边的比叫做相似比
对应角相等,对应边成比例
图形的相似
相似多边形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
27.1.1 图形的相似
人教版九年级下册
第二十七章 相似
1、经历相似图形概念的形成过程,了解相似图形的含义。
2、进一步发展自己归纳、类比、反思、交流等方面的能力。
3、在解决问题过程中体会学习数学的乐趣,在独立思考的基础上,敢于发表自己的观点并尊重他人的见解。
重点:理解邻补角和对顶角的概念.
难点:探索相交线对顶角之间的关系.
学习目标
重点难点
我们刚才所见到的图形有什么相同点和不同点
相同点:
不同点:
形状相同.
大小不一定相同.
生活中我们会碰到许多这样形状相同的.大小不一定相同的图形,
在数学上,我们把具有相同形状的图形称为:相似图形
1.相似图形只与图形的形状有关 ,与图形的____、____无关。
2.全等图形___相似图形,是相似图形的特例。
3.两个图形相似,其中一个图形可以看作是由另一个图形放大或缩小得到。
4、图形的相似具有传递性
大小
位置
是
如果图形A与图形B相似,图形B与图形C相似, 那么图形A与图形C相似。
如图是某个城市的大小不同的两张地图,当然,它们是相似的图形.设在大地图中有A、B、C三地,在小地图中的相应三地记为A′、B′、C′,试用刻度尺量一量两张地图中A(A′)与B(B′)两地之间的图上距离、B(B′)与C(C′)两地之间的图上距离.
AB=______cm, BC=______cm;
A′B′=______cm, B′C′=______cm.
显然两张地图中AB和A′B′、BC和B′C′的长度都是不相等的,那么它们之间有什么关系呢?小地图是由大地图缩小得来的,我们能感到线段A′B′、B′C′与AB、BC的长度相比都“同样程度”地缩小了.
=____,
=____.
也就是说上面地图中AB、A′B′、BC、B′C′这四条线段是成比例线段.
想一想:线段AC与A′C′的比是否也等于AB与A′B′的比呢?
实际上,上面两张相似的地图中的对应线段都是成比例的.
猜想: ____ ____ ____ ____ ____。
思考:这样的结论对一般的相似多边形是否成立呢?
=
我们能发现:
想一想:
如果在这两张地图中
AB:A`B`≠BC:B`C`,那么会出现什么情况?
图中两个四边形是相似形,仔细观察这两个图形,它们的对应边之间是否有以上的关系呢?对应角之间又有什么关系?
为了验证你的猜想是否正确,可以用量角器量量看
相似多边形的性质:
相似多边形对应边成比例,对应角相等.
剖析:
(1)两个多边形的边数不同一定不是相似多边形;
(2)定义中“角对应相等”、“边对应成比例”是判定两个多边形是否相似的必备的条件,缺一不可。
两个三角形一定是相似图形吗?两个等腰三角形呢?两个等边三角形呢?
两个三角形不一定是相似图形
两个等腰三角形不一定是相似图形
两个等边三角形一定是相似图形
例、在图所示的相似四边形中,求未知边x的长度和角α的大小.
解: ∵ 两个四边形相似,
∴ 18:12=X:18;
∴ 12X=18×18;
即 X=27。
根据对应角相等,可得:
α =360 °-(77 °+83 °+116 °)=84 °
E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1,求矩形ABCD的面积。
1.制作一块3mX2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
C
2.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边为( )
A.3cm B.4cm C.4.5cm D.5cm
C
A
A
3.相似多边形对应边之比叫做___________.
4.两个相似多边形的最长边分别为10cm和20cm,其中一个多边形的最短边为5cm,则另一个多边形的最短边为 .
相似比
5. 梯形ABCD中,AD∥BC,E,F分别为AB,CD上一点,且梯形AEFD∽梯形EBCF,若AD=4,BC=9。试求AE:EB的值。
相似图形
形状相同的图形叫做相似图形
相似图形的大小不一定相同
相似多边形对应边的比叫做相似比
对应角相等,对应边成比例
图形的相似
相似多边形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
