【原创精品】人教版数学九年级下册 27.2.1.1 《相似三角形的判定1》课件 (共23张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 27.2.1.1 《相似三角形的判定1》课件 (共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览




文档简介
(共23张PPT)
27.2.1.1 相似三角形的判定1
人教版九年级下册
第二十七章 相似
1、平行线分线段成比例定理及其推论。
2、会应用平行线分线段成比例定理写比例式、计算。
3、经历探究平行线分线段成比例定理的过程,培养分析归纳能力。
重点:掌握平行线分线段成比例的基本事实及其推论的应用.
难点:灵活运用平行线分线段成比例定理及其推论解决有关问题.
学习目标
重点难点
如图,在作业本上任意画一条直线m与相邻的三条平行线交于A、B、C三点,得到两条线段AB、BC,再任意画一条直线n与这组平行线相交,得到两条线段DE和EF,我们能发现什么呢?
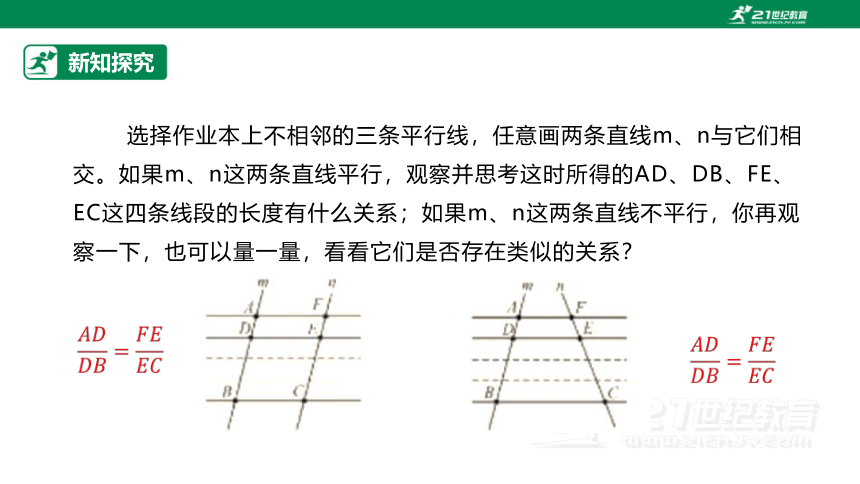
选择作业本上不相邻的三条平行线,任意画两条直线m、n与它们相交。如果m、n这两条直线平行,观察并思考这时所得的AD、DB、FE、EC这四条线段的长度有什么关系;如果m、n这两条直线不平行,你再观察一下,也可以量一量,看看它们是否存在类似的关系?
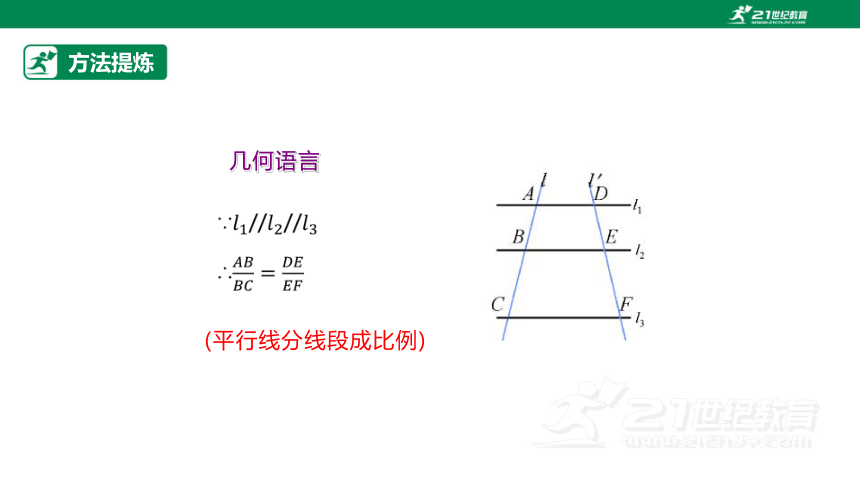
两条直线被一组平行线所截,所得的对应线段成比例.
(简称“平行线分线段成比例”)
几何语言
(平行线分线段成比例)
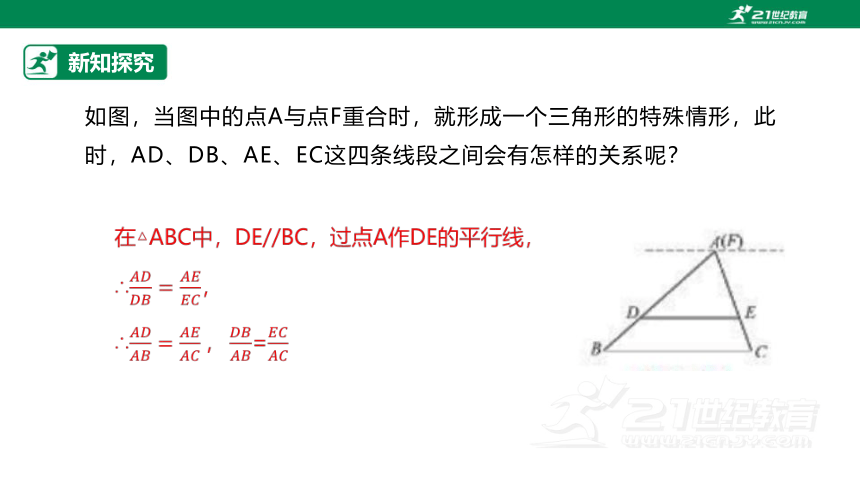
如图,当图中的点A与点F重合时,就形成一个三角形的特殊情形,此时,AD、DB、AE、EC这四条线段之间会有怎样的关系呢?
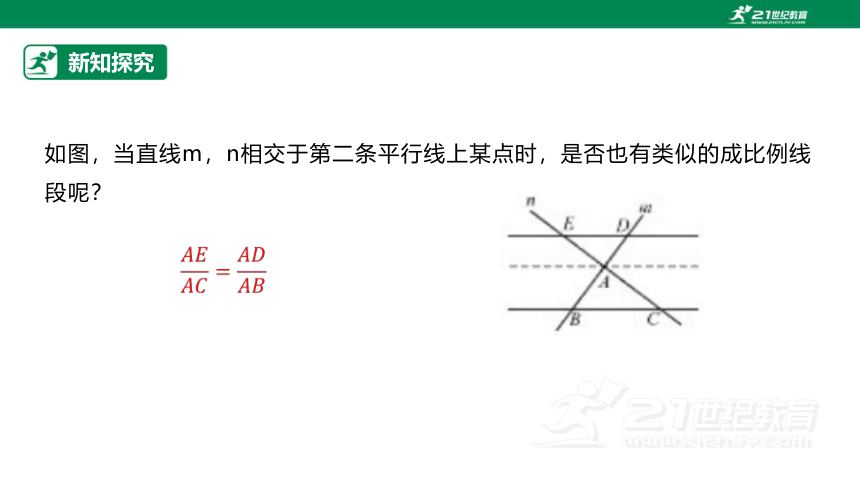
如图,当直线m,n相交于第二条平行线上某点时,是否也有类似的成比例线段呢?
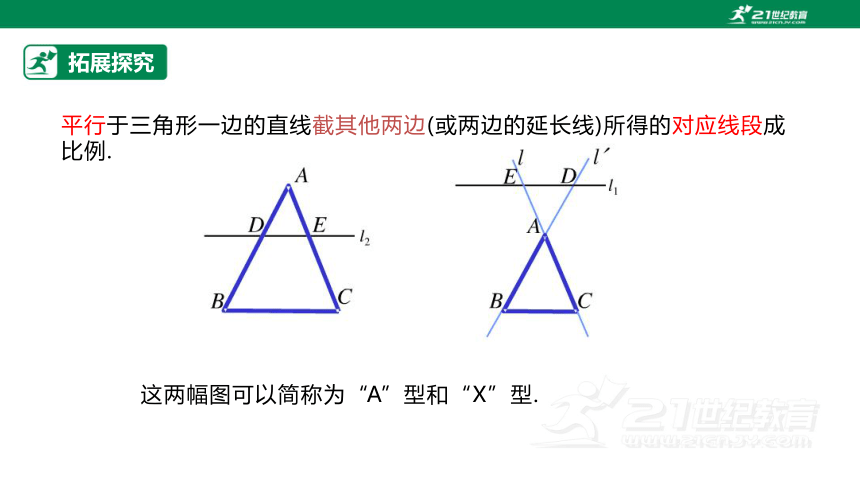
这两幅图可以简称为“A”型和“X”型.
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
几何语言
几何语言
在图中,DE//AF//BC,根据上面的结论,试找出图中成比例的线段
证明:
∵AF//BC
∵AB//CE
已知,l1//l2//l3,AB=4,DE=3,EF=6.求BC的长.
解:∵ l1//l2//l3
∵AB=4,DE=3,EF=6,
∴BC=8
A
如图,在△ABC中,DE∥BC,DE 分别与AB,AC 相交于点D,E,若AD=4,DB=2,则DE:BC的值为( )
A. B. C. D.
B
D
9
4.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
5.如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2,BC=8.求BF和CF的长。
6.如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,求EF.
两条直线被一组平行线所截,所得的对应线段成比例.
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
相似三角形判定的引理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
基本事实
平行线分线段成比例定理及其推论
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
27.2.1.1 相似三角形的判定1
人教版九年级下册
第二十七章 相似
1、平行线分线段成比例定理及其推论。
2、会应用平行线分线段成比例定理写比例式、计算。
3、经历探究平行线分线段成比例定理的过程,培养分析归纳能力。
重点:掌握平行线分线段成比例的基本事实及其推论的应用.
难点:灵活运用平行线分线段成比例定理及其推论解决有关问题.
学习目标
重点难点
如图,在作业本上任意画一条直线m与相邻的三条平行线交于A、B、C三点,得到两条线段AB、BC,再任意画一条直线n与这组平行线相交,得到两条线段DE和EF,我们能发现什么呢?
选择作业本上不相邻的三条平行线,任意画两条直线m、n与它们相交。如果m、n这两条直线平行,观察并思考这时所得的AD、DB、FE、EC这四条线段的长度有什么关系;如果m、n这两条直线不平行,你再观察一下,也可以量一量,看看它们是否存在类似的关系?
两条直线被一组平行线所截,所得的对应线段成比例.
(简称“平行线分线段成比例”)
几何语言
(平行线分线段成比例)
如图,当图中的点A与点F重合时,就形成一个三角形的特殊情形,此时,AD、DB、AE、EC这四条线段之间会有怎样的关系呢?
如图,当直线m,n相交于第二条平行线上某点时,是否也有类似的成比例线段呢?
这两幅图可以简称为“A”型和“X”型.
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
几何语言
几何语言
在图中,DE//AF//BC,根据上面的结论,试找出图中成比例的线段
证明:
∵AF//BC
∵AB//CE
已知,l1//l2//l3,AB=4,DE=3,EF=6.求BC的长.
解:∵ l1//l2//l3
∵AB=4,DE=3,EF=6,
∴BC=8
A
如图,在△ABC中,DE∥BC,DE 分别与AB,AC 相交于点D,E,若AD=4,DB=2,则DE:BC的值为( )
A. B. C. D.
B
D
9
4.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
5.如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2,BC=8.求BF和CF的长。
6.如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,求EF.
两条直线被一组平行线所截,所得的对应线段成比例.
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
相似三角形判定的引理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
基本事实
平行线分线段成比例定理及其推论
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
