【原创精品】人教版数学九年级下册 27.2.1.4 《相似三角形的判定4》课件 (共28张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 27.2.1.4 《相似三角形的判定4》课件 (共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览





文档简介
(共28张PPT)
27.2.1.4 相似三角形的判定4
人教版九年级下册
第二十七章 相似
1、掌握“两角对应相等,两个三角形相似”的判定方法.
2、能够运用三角形相似的条件解决简单的问题.
3、掌握判定两个直角三角形相似的方法,并能进行相关计算与推理.
重点:掌握“两角对应相等,两个三角形相似”的判定方法.
难点:能够运用三角形相似的条件解决简单的问题.
学习目标
重点难点
1.相似多边形的性质:
2.相似多边形的判定:
对应角相等,对应边成比例.
在两个多边形中,如果他们对应角相等,对应边成比例,那么这两个多边形相似.
全等三角形的判定方法有:____,____,____,____,直角三角形除此之外再加____.
SSS SAS ASA AAS
HL
那么,两个三角形至少满足哪些条件就相似呢 能否类比两个三角形全等的条件,寻找判定两个三角形相似的条件呢
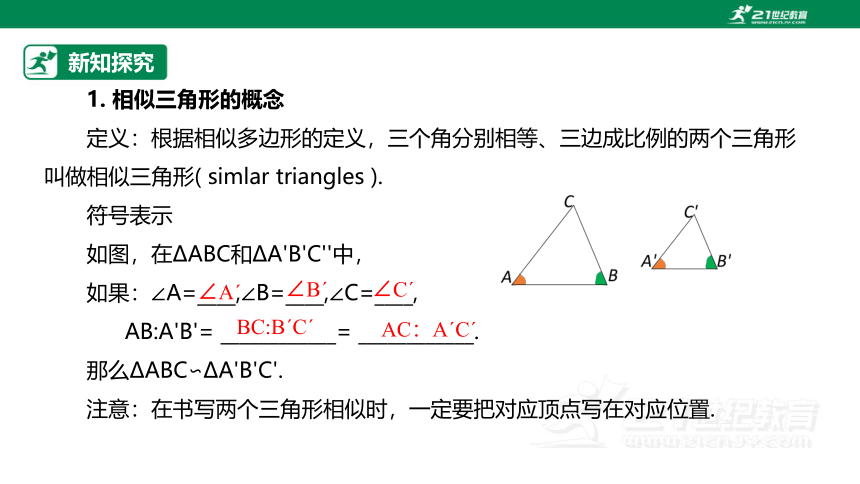
1. 相似三角形的概念
定义:根据相似多边形的定义,三个角分别相等、三边成比例的两个三角形叫做相似三角形( simlar triangles ).
符号表示
如图,在 ABC和 A'B'C''中,
如果:∠A=____,∠B=____,∠C=____,
AB:A'B'= ____________= ____________.
那么 ABC∽ A'B'C'.
注意:在书写两个三角形相似时,一定要把对应顶点写在对应位置.
BC:BˊCˊ
∠Bˊ
∠Cˊ
AC:AˊCˊ
∠Aˊ
2. 相似三角形的判定方法
(1) 观察只有一个角相等的三角形相似吗?与同伴交流.
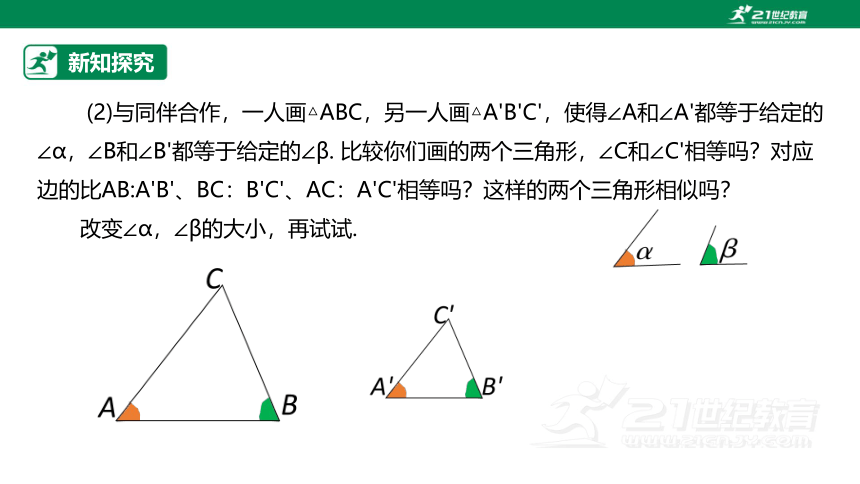
(2)与同伴合作,一人画△ABC,另一人画△A'B'C',使得∠A和∠A'都等于给定的∠α,∠B和∠B'都等于给定的∠β. 比较你们画的两个三角形,∠C和∠C'相等吗?对应边的比AB:A'B'、BC:B'C'、AC:A'C'相等吗?这样的两个三角形相似吗?
改变∠α,∠β的大小,再试试.
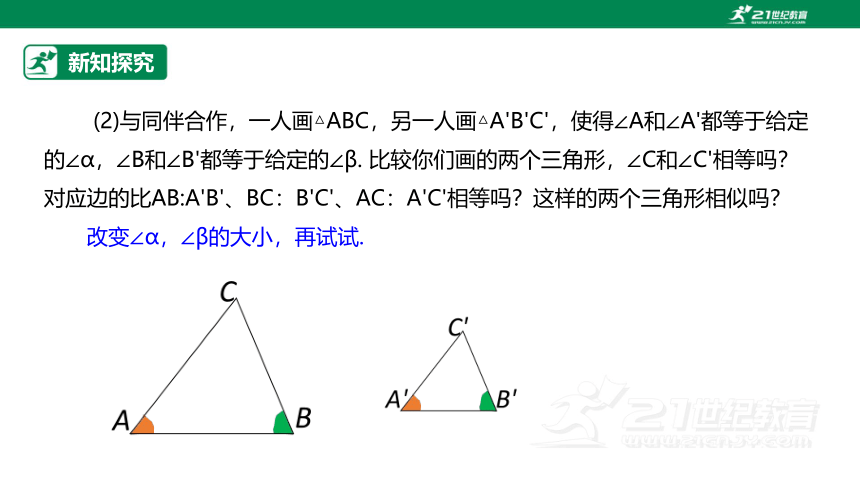
(2)与同伴合作,一人画△ABC,另一人画△A'B'C',使得∠A和∠A'都等于给定的∠α,∠B和∠B'都等于给定的∠β. 比较你们画的两个三角形,∠C和∠C'相等吗?对应边的比AB:A'B'、BC:B'C'、AC:A'C'相等吗?这样的两个三角形相似吗?
改变∠α,∠β的大小,再试试.
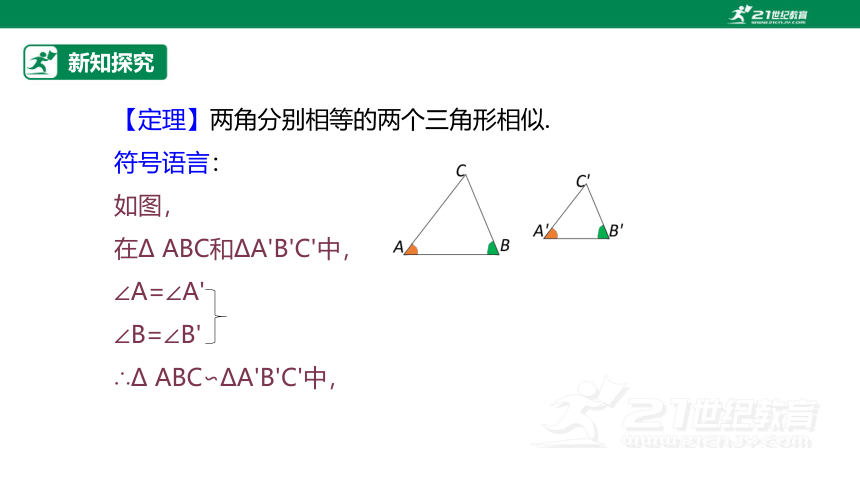
【定理】两角分别相等的两个三角形相似.
符号语言:
如图,
在 ABC和 A'B'C'中,
∠A=∠A'
∠B=∠B'
∴ ABC∽ A'B'C'中,
利用两角分别相等判定两个三角形相似,关键在于找准对应角,一般的,公共角、对顶角同角(或等角)余角或补角都是对应角.解题要注意挖掘题中的隐含条件.
核心总结
1. 利用“有两角相等的两个三角形相似”证明和计算
例1 如图,已知AB//CD,AD 、BC相交于点E,点F为EC上一点,且∠EAF=∠C.
求证:AF =FE FB.
证明: ∵ AB//CD, ∴∠B=∠C.
又∵∠EAF=∠C,
∴∠EAF=∠B.
又∵∠AFE=∠BFA,
∴ AFE∽ BFA
∴EF:AF=AF:BF,
∴AF =FE FB.
(1)利用相似三角形证明等积式或比例式时,把等积式或比例式中的四条线段分别看成两个三角形的对应边,然后证明这两个三角形相似,从而得到所要证明的结果.
(2)当两个三角形已经具备一个角对应相等的条件时,往往先找是否有另一个角相等,找角相等时应当注意挖据隐含的角,如公共角、对顶角、同角的余角(或补角)
等积与相似证明题总结
如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E.若AD=4,DB=2,则DE:BC的值为( )
A.2/3 B.1/2 C.3/4 D.3/5
A
2. 直角三角形中常见的相似问题
例2 CD是Rt ABC斜边AB上的高.
⑴已知AD=9 cm,CD=6 cm,求BD的长.
⑵已知AB=25 cm,BC=15 cm,求BD的长.
解: ∵△ABC是直角三角形,CD是斜边AB上的高,
∴∠ACB=∠ADC=∠BDC=90°
∠A+∠B=∠A+∠ACD=∠B+∠BCD=90°
∠A=∠BCD,∠B=∠ACD,
∴△ABC∽△ACD∽△CBD.
(1) ∵△ACD∽△CBD
∴AD:CD=CD:BD,即9:6=6:BD
∴BD=4 cm
2. 直角三角形中常见的相似问题
例2 CD是Rt ABC斜边AB上的高.
⑴已知AD=9 cm,CD=6 cm,求BD的长.
⑵已知AB=25 cm,BC=15 cm,求BD的长.
解: ∵△ABC是直角三角形,CD是斜边AB上的高,
∴∠ACB=∠ADC=∠BDC=90°
∠A+∠B=∠A+∠ACD=∠B+∠BCD=90°
∠A=∠BCD,∠B=∠ACD,
∴△ABC∽△ACD∽△CBD.
(2) ∵△CBD∽△ABC,
BC:BA=BD:BC,即15:25=BD:15,
BD=9 cm
直角三角形被斜边上的高分成的两个直角三角形与原三角形相似,可以归纳为”子母型”相似三角形,由于应用相当广泛,应重视这类常见的相似图形.
解题模型
如图,在正方形ABCD中,M为BC上点,F是AM的中点,EF⊥AM,垂足为点F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长
(1)证明: ∵四边形ABCD是正方形,
∴AB=AD,∠B=90°
∴AD∥BC
∠AMB=∠EAF
∵EF⊥AM, ∴∠AFE=90°,
∠B=∠AFE,△ABM∽△EFA
如图,在正方形ABCD中,M为BC上点,F是AM的中点,EF⊥AM,垂足为点F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长
(2)解:∠B=90°,AB=12,BM=5,
∴由勾股定理得AM=13,
∴AD=AB=12
∵F是AM的中点AF= AM=6.5
∵△ABM∽△EFA
∴BM:AF=AM:AE,即5:6.5=13:AE,
∴ AE=16.9.
∴ DE=AE-AD=4.9.
阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图①,在△ABC中,AD平分∠BAC,则AB:AC=BD:CD.下面是这个定理的部分证明过程.
证明:如图②,过点C作CE∥DA,交BA的延长线于点E. 任务:
(1)请按照上面的证明思路,写出该证明过程的剩余部分;
(2)填空:如图③,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是________.
解: (1)如题图②,过点C作CE∥DA.交BA的延长线于点E,
∴BD:CD=AB:AE,∠2=∠ACE,∠1=∠E,
∵∠1=∠2, ∴∠ACE=∠E,
∴AE=AC,
∴AB:AC=BD:CD.
阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图①,在△ABC中,AD平分∠BAC,则AB:AC=BD:CD.下面是这个定理的部分证明过程.
证明:如图②,过点C作CE∥DA,交BA的延长线于点E. 任务:
(1)请按照上面的证明思路,写出该证明过程的剩余部分;
(2)填空:如图③,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是________.
解: (2) ∵AB=3,BC=4,∠ABC=90°,∴AC=5.
∵AD平分∠BAC,
∴AC:AB=CD:BD,即5:3=CD:BD,
∴BD=3/8 BC=3/2,
∴AD= BD +AB =(3/2) +3 =
∴△ABD的周长=3/2+3+
1.如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为( )
A.2 B.4 C.6 D.8
B
2.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为( )
A.0.2m B.0.3m C.0.4m D.0.5m
C
1.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形( )
A.一定不相似 B.不一定相似
C.一定相似 D.不能确定
2.下列说法中正确的是( )
A.两个直角三角形相似 B.两个等腰三角形相似
C.两个等边三角形相似 D.两个锐角三角形相似
C
C
3.如图,在△ABC中,点D,E分别在边AB,AC上.若DE∥BC,AD=3,AB=5,求DE:BC的值.
解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
则△ADE∽△ABC,
DE;BC=AD:AB=3:5
4.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE
证明:在△ABC中,AB=AC,BD=CD,∴AD⊥BC.
∵CE⊥AB,
∴∠ADB=∠CEB=90°.
又∵∠B=∠B,
∴△ABD∽△CBE.
相似三角形的判定
定理
几何语言
两角分别对应相等的两个三角形相似。
∵ ∠A=∠D
∠B=∠E
∴ΔABC∽ΔDEF
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
27.2.1.4 相似三角形的判定4
人教版九年级下册
第二十七章 相似
1、掌握“两角对应相等,两个三角形相似”的判定方法.
2、能够运用三角形相似的条件解决简单的问题.
3、掌握判定两个直角三角形相似的方法,并能进行相关计算与推理.
重点:掌握“两角对应相等,两个三角形相似”的判定方法.
难点:能够运用三角形相似的条件解决简单的问题.
学习目标
重点难点
1.相似多边形的性质:
2.相似多边形的判定:
对应角相等,对应边成比例.
在两个多边形中,如果他们对应角相等,对应边成比例,那么这两个多边形相似.
全等三角形的判定方法有:____,____,____,____,直角三角形除此之外再加____.
SSS SAS ASA AAS
HL
那么,两个三角形至少满足哪些条件就相似呢 能否类比两个三角形全等的条件,寻找判定两个三角形相似的条件呢
1. 相似三角形的概念
定义:根据相似多边形的定义,三个角分别相等、三边成比例的两个三角形叫做相似三角形( simlar triangles ).
符号表示
如图,在 ABC和 A'B'C''中,
如果:∠A=____,∠B=____,∠C=____,
AB:A'B'= ____________= ____________.
那么 ABC∽ A'B'C'.
注意:在书写两个三角形相似时,一定要把对应顶点写在对应位置.
BC:BˊCˊ
∠Bˊ
∠Cˊ
AC:AˊCˊ
∠Aˊ
2. 相似三角形的判定方法
(1) 观察只有一个角相等的三角形相似吗?与同伴交流.
(2)与同伴合作,一人画△ABC,另一人画△A'B'C',使得∠A和∠A'都等于给定的∠α,∠B和∠B'都等于给定的∠β. 比较你们画的两个三角形,∠C和∠C'相等吗?对应边的比AB:A'B'、BC:B'C'、AC:A'C'相等吗?这样的两个三角形相似吗?
改变∠α,∠β的大小,再试试.
(2)与同伴合作,一人画△ABC,另一人画△A'B'C',使得∠A和∠A'都等于给定的∠α,∠B和∠B'都等于给定的∠β. 比较你们画的两个三角形,∠C和∠C'相等吗?对应边的比AB:A'B'、BC:B'C'、AC:A'C'相等吗?这样的两个三角形相似吗?
改变∠α,∠β的大小,再试试.
【定理】两角分别相等的两个三角形相似.
符号语言:
如图,
在 ABC和 A'B'C'中,
∠A=∠A'
∠B=∠B'
∴ ABC∽ A'B'C'中,
利用两角分别相等判定两个三角形相似,关键在于找准对应角,一般的,公共角、对顶角同角(或等角)余角或补角都是对应角.解题要注意挖掘题中的隐含条件.
核心总结
1. 利用“有两角相等的两个三角形相似”证明和计算
例1 如图,已知AB//CD,AD 、BC相交于点E,点F为EC上一点,且∠EAF=∠C.
求证:AF =FE FB.
证明: ∵ AB//CD, ∴∠B=∠C.
又∵∠EAF=∠C,
∴∠EAF=∠B.
又∵∠AFE=∠BFA,
∴ AFE∽ BFA
∴EF:AF=AF:BF,
∴AF =FE FB.
(1)利用相似三角形证明等积式或比例式时,把等积式或比例式中的四条线段分别看成两个三角形的对应边,然后证明这两个三角形相似,从而得到所要证明的结果.
(2)当两个三角形已经具备一个角对应相等的条件时,往往先找是否有另一个角相等,找角相等时应当注意挖据隐含的角,如公共角、对顶角、同角的余角(或补角)
等积与相似证明题总结
如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E.若AD=4,DB=2,则DE:BC的值为( )
A.2/3 B.1/2 C.3/4 D.3/5
A
2. 直角三角形中常见的相似问题
例2 CD是Rt ABC斜边AB上的高.
⑴已知AD=9 cm,CD=6 cm,求BD的长.
⑵已知AB=25 cm,BC=15 cm,求BD的长.
解: ∵△ABC是直角三角形,CD是斜边AB上的高,
∴∠ACB=∠ADC=∠BDC=90°
∠A+∠B=∠A+∠ACD=∠B+∠BCD=90°
∠A=∠BCD,∠B=∠ACD,
∴△ABC∽△ACD∽△CBD.
(1) ∵△ACD∽△CBD
∴AD:CD=CD:BD,即9:6=6:BD
∴BD=4 cm
2. 直角三角形中常见的相似问题
例2 CD是Rt ABC斜边AB上的高.
⑴已知AD=9 cm,CD=6 cm,求BD的长.
⑵已知AB=25 cm,BC=15 cm,求BD的长.
解: ∵△ABC是直角三角形,CD是斜边AB上的高,
∴∠ACB=∠ADC=∠BDC=90°
∠A+∠B=∠A+∠ACD=∠B+∠BCD=90°
∠A=∠BCD,∠B=∠ACD,
∴△ABC∽△ACD∽△CBD.
(2) ∵△CBD∽△ABC,
BC:BA=BD:BC,即15:25=BD:15,
BD=9 cm
直角三角形被斜边上的高分成的两个直角三角形与原三角形相似,可以归纳为”子母型”相似三角形,由于应用相当广泛,应重视这类常见的相似图形.
解题模型
如图,在正方形ABCD中,M为BC上点,F是AM的中点,EF⊥AM,垂足为点F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长
(1)证明: ∵四边形ABCD是正方形,
∴AB=AD,∠B=90°
∴AD∥BC
∠AMB=∠EAF
∵EF⊥AM, ∴∠AFE=90°,
∠B=∠AFE,△ABM∽△EFA
如图,在正方形ABCD中,M为BC上点,F是AM的中点,EF⊥AM,垂足为点F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长
(2)解:∠B=90°,AB=12,BM=5,
∴由勾股定理得AM=13,
∴AD=AB=12
∵F是AM的中点AF= AM=6.5
∵△ABM∽△EFA
∴BM:AF=AM:AE,即5:6.5=13:AE,
∴ AE=16.9.
∴ DE=AE-AD=4.9.
阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图①,在△ABC中,AD平分∠BAC,则AB:AC=BD:CD.下面是这个定理的部分证明过程.
证明:如图②,过点C作CE∥DA,交BA的延长线于点E. 任务:
(1)请按照上面的证明思路,写出该证明过程的剩余部分;
(2)填空:如图③,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是________.
解: (1)如题图②,过点C作CE∥DA.交BA的延长线于点E,
∴BD:CD=AB:AE,∠2=∠ACE,∠1=∠E,
∵∠1=∠2, ∴∠ACE=∠E,
∴AE=AC,
∴AB:AC=BD:CD.
阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图①,在△ABC中,AD平分∠BAC,则AB:AC=BD:CD.下面是这个定理的部分证明过程.
证明:如图②,过点C作CE∥DA,交BA的延长线于点E. 任务:
(1)请按照上面的证明思路,写出该证明过程的剩余部分;
(2)填空:如图③,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是________.
解: (2) ∵AB=3,BC=4,∠ABC=90°,∴AC=5.
∵AD平分∠BAC,
∴AC:AB=CD:BD,即5:3=CD:BD,
∴BD=3/8 BC=3/2,
∴AD= BD +AB =(3/2) +3 =
∴△ABD的周长=3/2+3+
1.如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为( )
A.2 B.4 C.6 D.8
B
2.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为( )
A.0.2m B.0.3m C.0.4m D.0.5m
C
1.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形( )
A.一定不相似 B.不一定相似
C.一定相似 D.不能确定
2.下列说法中正确的是( )
A.两个直角三角形相似 B.两个等腰三角形相似
C.两个等边三角形相似 D.两个锐角三角形相似
C
C
3.如图,在△ABC中,点D,E分别在边AB,AC上.若DE∥BC,AD=3,AB=5,求DE:BC的值.
解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
则△ADE∽△ABC,
DE;BC=AD:AB=3:5
4.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE
证明:在△ABC中,AB=AC,BD=CD,∴AD⊥BC.
∵CE⊥AB,
∴∠ADB=∠CEB=90°.
又∵∠B=∠B,
∴△ABD∽△CBE.
相似三角形的判定
定理
几何语言
两角分别对应相等的两个三角形相似。
∵ ∠A=∠D
∠B=∠E
∴ΔABC∽ΔDEF
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
