【原创精品】人教版数学九年级下册 27.2.1.2 《相似三角形的判定2》课件 (共43张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 27.2.1.2 《相似三角形的判定2》课件 (共43张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览








文档简介
(共43张PPT)
27.2.1.2 相似三角形的判定2
人教版九年级下册
第二十七章 相似
1、掌握“三边对应成比例,两个三角形相似”的判定方法.并初步应用。
2、通过类比观察、猜想、证明等活动,探索相似三角形判定定理证明的过程体会转化的数学思想。
3、进一步积累研究几何图形问题的经验。
重点:“三边对应成比例,两个三角形相似”判定定理的证明及初步应用.
难点:相似三角形判定定理证明过程中在比例式中得到线段相等的关系.
学习目标
重点难点
对应角相等,对应边成比例
的两个三角形叫做相似三角形.
1.定义法:
∵∠A=∠A',∠B=∠B',∠C=∠C'
符号语言:
1.定义法:
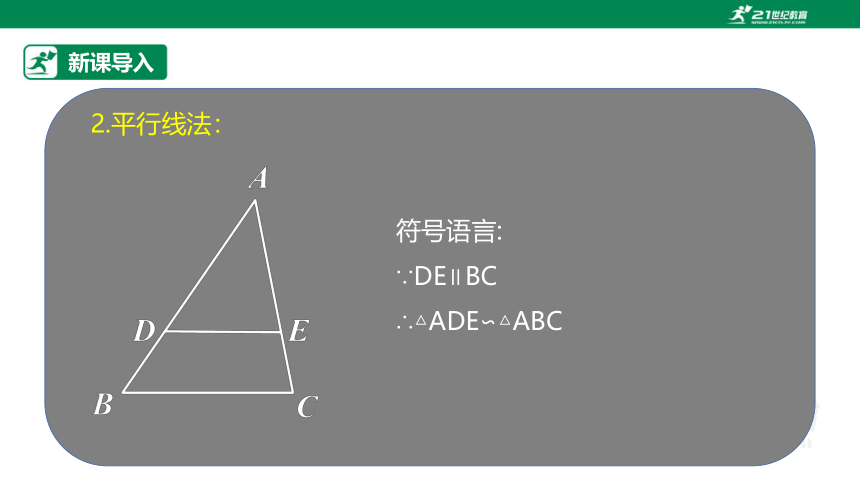
平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
2.平行线法:
符号语言:
∵DE∥BC
∴△ADE∽△ABC
2.平行线法:
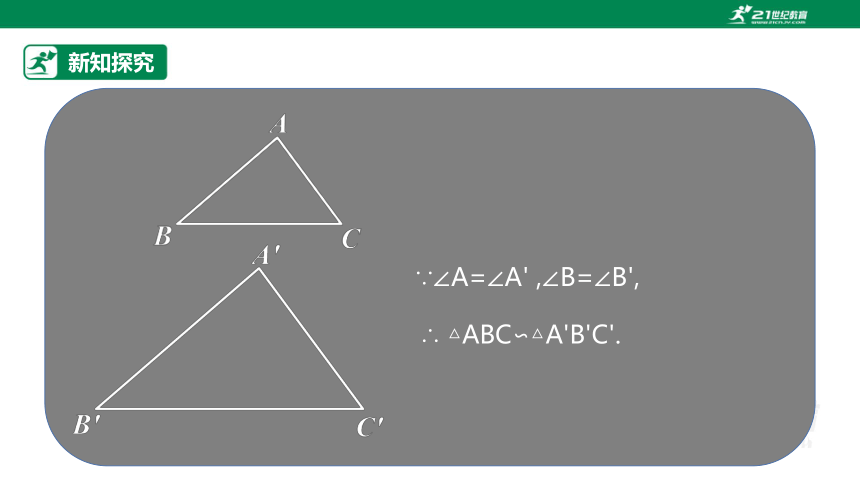
两角分别相等,两三角形相似.
3.相似三角形的判定定理:
符号语言:
∵∠A=∠A',∠B=∠B' ∴△ABC∽△A'B'C'.
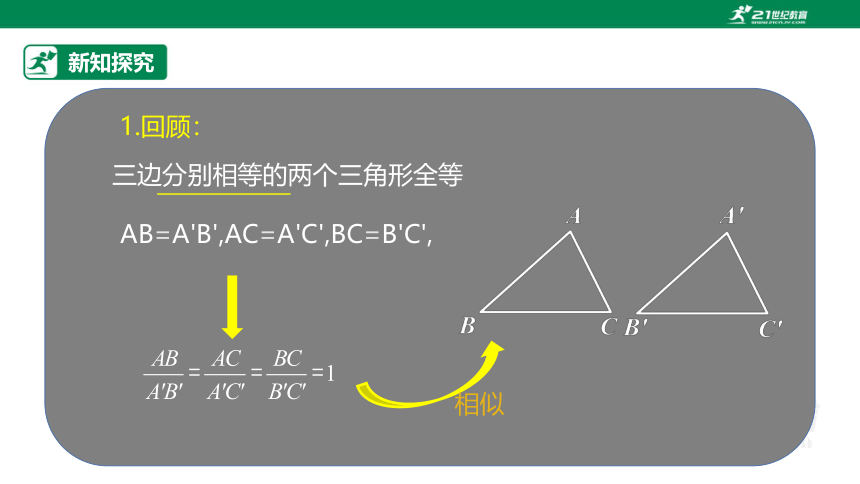
1.回顾:
三边分别相等的两个三角形全等
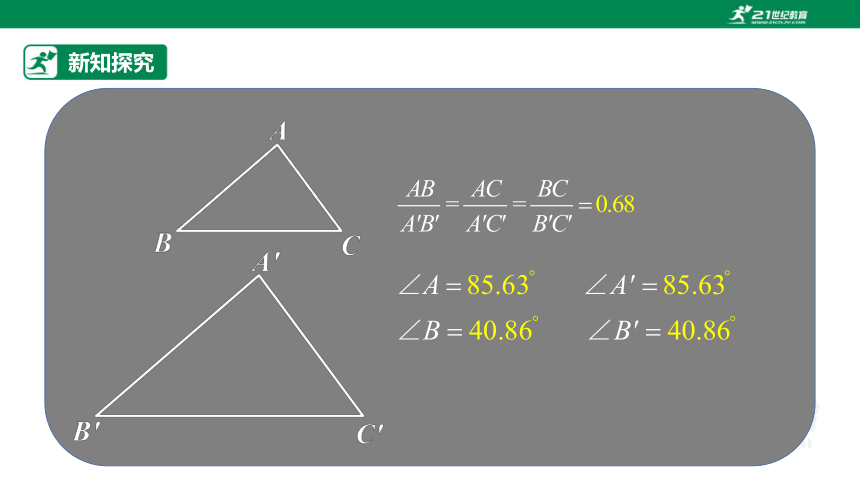
2.延伸问题:
∵∠A=∠A' ,∠B=∠B',
改变k值的大小,再试一试.
改变k值的大小,再试一试.
∵∠A=∠A',∠B=∠B',
已知:如图,在△ABC与△A'B'C'中,
求证:△ABC∽△A'B'C'.
猜想:
如果两个三角形中,三边对应成比例,那么这两个三角形相似.
在AB上截取AD=A'B'
过点D作DE∥BC交AC于点E
D
E
△ABC∽△ADE
分析:
D
E
△ABC∽△ADE
D
E
AD=A'B'.
证明:
过点D作DE∥BC交AC于点E.
∴△ABC∽△ADE,
D
E
∴△ADE≌△A'B'C'.
∴△ABC∽△A'B'C'.
如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
相似三角形的判定定理
(三边对应成比例,两三角形相似)
(1)通过类比学习,把未知问题转化为已知问题,体现了转化和类比思想,这两种思想方法也是学习数学过程中常用的思想方法.
(2)本节课的课堂练习,体现了分类讨论的学习方法,这种方法能够使我们解决问题时考虑的更加全面.
相似三角形的判定定理
∴△ABC∽△A'B'C'.
∴△ABC∽△A'B'C'.
解:
∴△ABC与△A'B'C'不相似.
解:
如下图所示,在正方形网格上有两个三角形,△ABC和△DEF,它们相似吗?说明理由.
每个小方形的边长为1
∴△ABC∽△DEF.
∴BC=5,DE=2,
解:设每个小方形的边长为1
∴△ABC∽△DEF.
如图,小正方形的边长均为1,则下列图中的三
角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
B
4cm
5cm
6cm
(3)如果边长为4,5,6的对应边长分别为x,y,2,
那么:
解得:
(2)如果边长为4,5,6的对应边长分别为x,2,y,
那么:
解得:
2.已知:点D,E,F分别是△ABC三边的中点.求证:△EFD∽△ABC.
证明:(证法一)
∵点D,E,F分别是△ABC三边的中点.
1.知识:
(1)定义:三个角分别相等,三条边对应成比例的两个三角形相似.
(2)平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
(3)判定定理:两角分别相等,两三角形相似.
(4)判定定理:三边对应成比例,两三角形相似.
(1)通过类比学习,把未知问题转化为已知问题,体现了转化和类比思想,这两种思想方法也是学习数学过程中常用的思想方法.
2.方法:
(2)本节课的课堂练习,体现了分类讨论的学习方法,这种方法能够使我们解决问题时考虑的更加全面.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
27.2.1.2 相似三角形的判定2
人教版九年级下册
第二十七章 相似
1、掌握“三边对应成比例,两个三角形相似”的判定方法.并初步应用。
2、通过类比观察、猜想、证明等活动,探索相似三角形判定定理证明的过程体会转化的数学思想。
3、进一步积累研究几何图形问题的经验。
重点:“三边对应成比例,两个三角形相似”判定定理的证明及初步应用.
难点:相似三角形判定定理证明过程中在比例式中得到线段相等的关系.
学习目标
重点难点
对应角相等,对应边成比例
的两个三角形叫做相似三角形.
1.定义法:
∵∠A=∠A',∠B=∠B',∠C=∠C'
符号语言:
1.定义法:
平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
2.平行线法:
符号语言:
∵DE∥BC
∴△ADE∽△ABC
2.平行线法:
两角分别相等,两三角形相似.
3.相似三角形的判定定理:
符号语言:
∵∠A=∠A',∠B=∠B' ∴△ABC∽△A'B'C'.
1.回顾:
三边分别相等的两个三角形全等
2.延伸问题:
∵∠A=∠A' ,∠B=∠B',
改变k值的大小,再试一试.
改变k值的大小,再试一试.
∵∠A=∠A',∠B=∠B',
已知:如图,在△ABC与△A'B'C'中,
求证:△ABC∽△A'B'C'.
猜想:
如果两个三角形中,三边对应成比例,那么这两个三角形相似.
在AB上截取AD=A'B'
过点D作DE∥BC交AC于点E
D
E
△ABC∽△ADE
分析:
D
E
△ABC∽△ADE
D
E
AD=A'B'.
证明:
过点D作DE∥BC交AC于点E.
∴△ABC∽△ADE,
D
E
∴△ADE≌△A'B'C'.
∴△ABC∽△A'B'C'.
如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
相似三角形的判定定理
(三边对应成比例,两三角形相似)
(1)通过类比学习,把未知问题转化为已知问题,体现了转化和类比思想,这两种思想方法也是学习数学过程中常用的思想方法.
(2)本节课的课堂练习,体现了分类讨论的学习方法,这种方法能够使我们解决问题时考虑的更加全面.
相似三角形的判定定理
∴△ABC∽△A'B'C'.
∴△ABC∽△A'B'C'.
解:
∴△ABC与△A'B'C'不相似.
解:
如下图所示,在正方形网格上有两个三角形,△ABC和△DEF,它们相似吗?说明理由.
每个小方形的边长为1
∴△ABC∽△DEF.
∴BC=5,DE=2,
解:设每个小方形的边长为1
∴△ABC∽△DEF.
如图,小正方形的边长均为1,则下列图中的三
角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
B
4cm
5cm
6cm
(3)如果边长为4,5,6的对应边长分别为x,y,2,
那么:
解得:
(2)如果边长为4,5,6的对应边长分别为x,2,y,
那么:
解得:
2.已知:点D,E,F分别是△ABC三边的中点.求证:△EFD∽△ABC.
证明:(证法一)
∵点D,E,F分别是△ABC三边的中点.
1.知识:
(1)定义:三个角分别相等,三条边对应成比例的两个三角形相似.
(2)平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
(3)判定定理:两角分别相等,两三角形相似.
(4)判定定理:三边对应成比例,两三角形相似.
(1)通过类比学习,把未知问题转化为已知问题,体现了转化和类比思想,这两种思想方法也是学习数学过程中常用的思想方法.
2.方法:
(2)本节课的课堂练习,体现了分类讨论的学习方法,这种方法能够使我们解决问题时考虑的更加全面.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
