【原创精品】人教版数学九年级下册 27.2.2 《相似三角形的性质》课件 (共28张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 27.2.2 《相似三角形的性质》课件 (共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览



文档简介
(共28张PPT)
27.2.2 相似三角形的性质
人教版九年级下册
第二十七章 相似
1、掌握相似三角形的性质.
2、会运用结论进行有关简单的计算.
3、发展合理推理能力,提高学习数学的兴趣和自信心.
重点:掌握相似三角形的性质.
难点:运用结论进行有关简单的计算.
学习目标
重点难点
相似三角形的判定
相似三角形的性质
相似三角形的判定:
(1)平行于三角形一边的直线截其他两边所得的三角形与原三角形相似 :
(2)( )对应相等的两个三角形相似:
(3)两边对应成比例且( )的两个三角形相似:
(4)三边对应( )的两个三角形相似
1.相似三角形的判定方法有哪些?
2.相似三角形有哪些性质?
3.三角形中的主要线段有哪些?
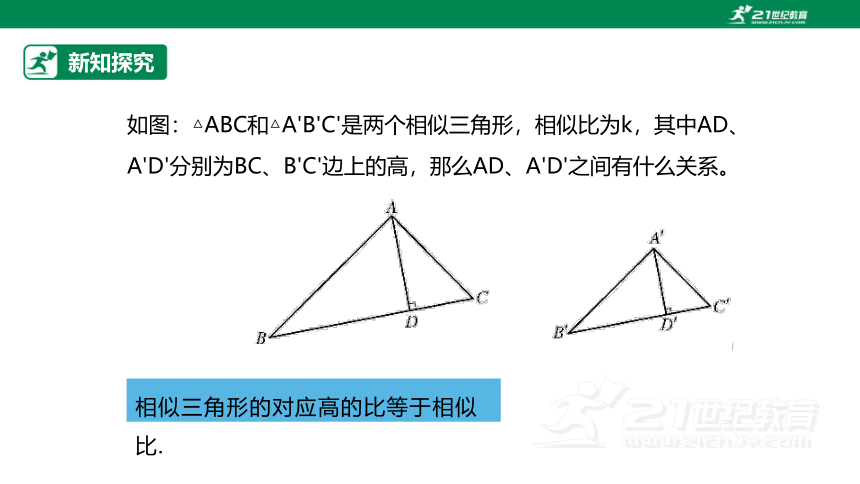
如图:△ABC和△A'B'C'是两个相似三角形,相似比为k,其中AD、A'D'分别为BC、B'C'边上的高,那么AD、A'D'之间有什么关系。
相似三角形的对应高的比等于相似比.
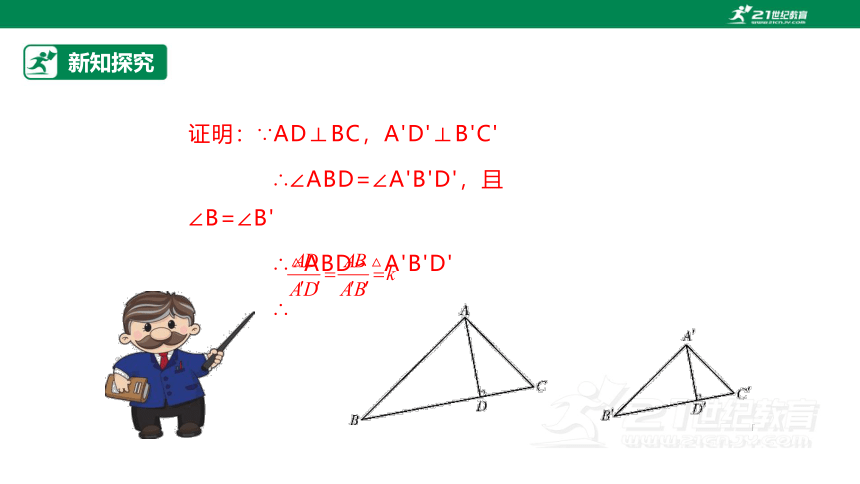
证明:∵AD⊥BC,A'D'⊥B'C'
∴∠ABD=∠A'B'D',且∠B=∠B'
∴△ABD∽△A'B'D'
∴
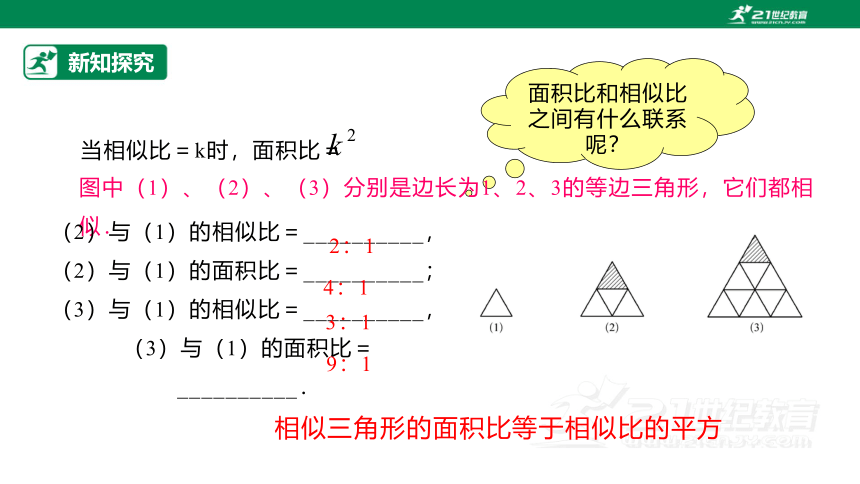
面积比和相似比之间有什么联系呢?
图中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,它们都相似.
(2)与(1)的相似比=__________,
(2)与(1)的面积比=__________;
(3)与(1)的相似比=__________,
(3)与(1)的面积比=__________.
2:1
4:1
3:1
9:1
当相似比=k时,面积比=
相似三角形的面积比等于相似比的平方
A
B
C
C’
A’
B’
D
D’
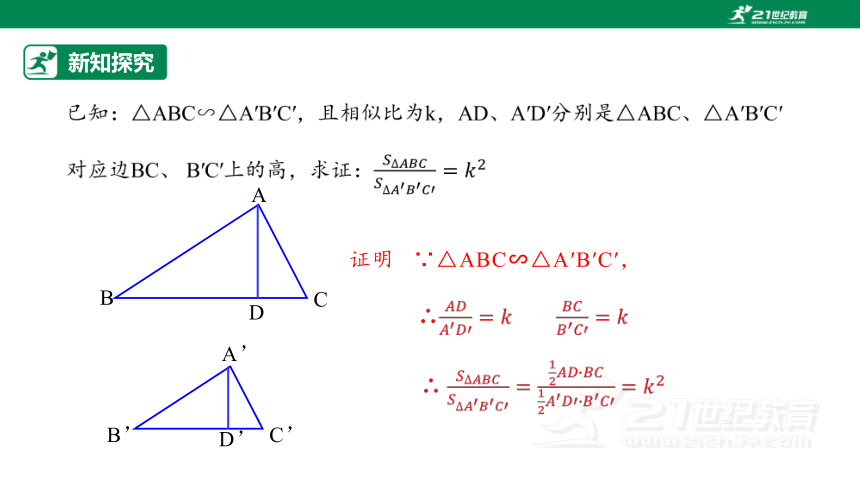
证明 ∵△ABC∽△A′B′C′,
图中,△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
两个相似三角形的周长比是什么?
相似三角形的周长比等于相似比
对应边上的中线的比等于相似比;对应角上的角平分线的比等于相似比。
相似三角形对应比的拓展
1、相似三角形对应高的比等于相似比.
2、相似三角形的面积比等于相似比的平方
3、相似三角形的周长比等于相似比
4、对应边上的中线的比等于相似比;
对应角上的角平分线的比等于相似比。
解:∵△ABC∽△DEF,
D
E
F
H
例1 已知△ABC∽△DEF,BG、EH分别是△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
A
G
B
C
∴故EH的长为3.2 cm.
1. 如果两个相似三角形的对应高的比为2:3,那么对应角平分线的比是 ,对应边上的中线的比是 ______ .
2. △ABC与△A'B'C'的相似比为3:4,若BC边上的高AD=12cm,则B'C'边上的高A'D'=_______ .
2 : 3
2 : 3
16 cm
∴△ADE∽△ABC.
∵它们的相似比为3:5,
∴面积比为9:25.
B
C
A
D
E
又∵△ABC的面积为100 cm2,
∴△ADE 的面积为36 cm2 .
∴四边形BCDE的面积为100-36=64 (cm2).
如图:四边形ABCD∽四边形A'B'C'D',相似比为k.
(相似多边形的对应角相等,对应边成比例)
四边形边的比
A
B
C
D
A'
B'
C'
D'
(2)四边形ABCD与四边形A'B'C'D'的周长比与相似比有什么关系?
测量、计算
猜想:相似四边形的周长比等于相似比
四边形周长的比
如图:四边形ABCD∽四边形A'B'C'D',相似比为k.
A
B
C
D
A'
B'
C'
D'
四边形周长的比
A
B
C
D
A'
B'
C'
D'
(3)四边形ABCD与四边形A'B'C'D'的面积比与相似比有什么关系?
测量、计算
猜想:相似四边形的面积比等于相似比的平方
四边形面积的比
如图:四边形ABCD∽四边形A'B'C'D',相似比为k.
A
B
C
D
A'
B'
C'
D'
A
B
C
D
A'
B'
C'
D'
四边形面积的比
如图:五边形ABCDE∽五边形A'B'C'D'E',相似比为k.
它们的周长比、面积比与相似比还有相同的结论吗?
A
B
C
D
E
A'
B'
C'
D'
E'
等量代换
提公因式
约分
五边形的比
思考:如果是相似n边形,相似比为k.
它们的周长比、面积比与相似比还有相同的结论吗?
n边之和的比
(n-2)个三角形面积之和的比
类比
相似多边形的周长比等于相似比,
面积比等于相似比的平方.
结论:
(中考·常州) △ABC ∽△A‘B’C‘ ,相似比为 1:2.则△ABC和△A’B‘C’的周长的比为( )
A.2:1 B.1:2 C.4:1 D.1:4
B
1. 判断:
(1) 一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍 ( )
(2) 一个四边形的各边长扩大为原来的9倍,这个 四边形的面积也扩大为原来的9倍 ( )
√
×
C
3. 连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_____.
1 : 2
1 : 4
4. 两个相似三角形对应的中线长分别是6 cm 和18 cm,若较大三角形的周长是42 cm,面积是12 cm2,则较小三角形的周长____cm,面积为____cm2.
14
5. △ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,求△ABC的面积.
解:∵ DE∥BC,EF∥AB,
∴ △ADE∽△ABC,
∠ADE=∠EFC,∠A=∠CEF,
∴△ADE∽△EFC.
又∵S△ADE : S△EFC = 4 : 9,
∴ AE : EC=2:3,
则 AE : AC =2 : 5,
∴ S△ADE : S△ABC = 4 : 25,∴ S△ABC = 25.
相似三角形的性质
1、相似三角形对应高的比等于相似比.
2、相似三角形的面积比等于相似比的平方
3、相似三角形的周长比等于相似比
4、对应边上的中线的比等于相似比;
对应角上的角平分线的比等于相似比。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
27.2.2 相似三角形的性质
人教版九年级下册
第二十七章 相似
1、掌握相似三角形的性质.
2、会运用结论进行有关简单的计算.
3、发展合理推理能力,提高学习数学的兴趣和自信心.
重点:掌握相似三角形的性质.
难点:运用结论进行有关简单的计算.
学习目标
重点难点
相似三角形的判定
相似三角形的性质
相似三角形的判定:
(1)平行于三角形一边的直线截其他两边所得的三角形与原三角形相似 :
(2)( )对应相等的两个三角形相似:
(3)两边对应成比例且( )的两个三角形相似:
(4)三边对应( )的两个三角形相似
1.相似三角形的判定方法有哪些?
2.相似三角形有哪些性质?
3.三角形中的主要线段有哪些?
如图:△ABC和△A'B'C'是两个相似三角形,相似比为k,其中AD、A'D'分别为BC、B'C'边上的高,那么AD、A'D'之间有什么关系。
相似三角形的对应高的比等于相似比.
证明:∵AD⊥BC,A'D'⊥B'C'
∴∠ABD=∠A'B'D',且∠B=∠B'
∴△ABD∽△A'B'D'
∴
面积比和相似比之间有什么联系呢?
图中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,它们都相似.
(2)与(1)的相似比=__________,
(2)与(1)的面积比=__________;
(3)与(1)的相似比=__________,
(3)与(1)的面积比=__________.
2:1
4:1
3:1
9:1
当相似比=k时,面积比=
相似三角形的面积比等于相似比的平方
A
B
C
C’
A’
B’
D
D’
证明 ∵△ABC∽△A′B′C′,
图中,△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
两个相似三角形的周长比是什么?
相似三角形的周长比等于相似比
对应边上的中线的比等于相似比;对应角上的角平分线的比等于相似比。
相似三角形对应比的拓展
1、相似三角形对应高的比等于相似比.
2、相似三角形的面积比等于相似比的平方
3、相似三角形的周长比等于相似比
4、对应边上的中线的比等于相似比;
对应角上的角平分线的比等于相似比。
解:∵△ABC∽△DEF,
D
E
F
H
例1 已知△ABC∽△DEF,BG、EH分别是△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
A
G
B
C
∴故EH的长为3.2 cm.
1. 如果两个相似三角形的对应高的比为2:3,那么对应角平分线的比是 ,对应边上的中线的比是 ______ .
2. △ABC与△A'B'C'的相似比为3:4,若BC边上的高AD=12cm,则B'C'边上的高A'D'=_______ .
2 : 3
2 : 3
16 cm
∴△ADE∽△ABC.
∵它们的相似比为3:5,
∴面积比为9:25.
B
C
A
D
E
又∵△ABC的面积为100 cm2,
∴△ADE 的面积为36 cm2 .
∴四边形BCDE的面积为100-36=64 (cm2).
如图:四边形ABCD∽四边形A'B'C'D',相似比为k.
(相似多边形的对应角相等,对应边成比例)
四边形边的比
A
B
C
D
A'
B'
C'
D'
(2)四边形ABCD与四边形A'B'C'D'的周长比与相似比有什么关系?
测量、计算
猜想:相似四边形的周长比等于相似比
四边形周长的比
如图:四边形ABCD∽四边形A'B'C'D',相似比为k.
A
B
C
D
A'
B'
C'
D'
四边形周长的比
A
B
C
D
A'
B'
C'
D'
(3)四边形ABCD与四边形A'B'C'D'的面积比与相似比有什么关系?
测量、计算
猜想:相似四边形的面积比等于相似比的平方
四边形面积的比
如图:四边形ABCD∽四边形A'B'C'D',相似比为k.
A
B
C
D
A'
B'
C'
D'
A
B
C
D
A'
B'
C'
D'
四边形面积的比
如图:五边形ABCDE∽五边形A'B'C'D'E',相似比为k.
它们的周长比、面积比与相似比还有相同的结论吗?
A
B
C
D
E
A'
B'
C'
D'
E'
等量代换
提公因式
约分
五边形的比
思考:如果是相似n边形,相似比为k.
它们的周长比、面积比与相似比还有相同的结论吗?
n边之和的比
(n-2)个三角形面积之和的比
类比
相似多边形的周长比等于相似比,
面积比等于相似比的平方.
结论:
(中考·常州) △ABC ∽△A‘B’C‘ ,相似比为 1:2.则△ABC和△A’B‘C’的周长的比为( )
A.2:1 B.1:2 C.4:1 D.1:4
B
1. 判断:
(1) 一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍 ( )
(2) 一个四边形的各边长扩大为原来的9倍,这个 四边形的面积也扩大为原来的9倍 ( )
√
×
C
3. 连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_____.
1 : 2
1 : 4
4. 两个相似三角形对应的中线长分别是6 cm 和18 cm,若较大三角形的周长是42 cm,面积是12 cm2,则较小三角形的周长____cm,面积为____cm2.
14
5. △ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,求△ABC的面积.
解:∵ DE∥BC,EF∥AB,
∴ △ADE∽△ABC,
∠ADE=∠EFC,∠A=∠CEF,
∴△ADE∽△EFC.
又∵S△ADE : S△EFC = 4 : 9,
∴ AE : EC=2:3,
则 AE : AC =2 : 5,
∴ S△ADE : S△ABC = 4 : 25,∴ S△ABC = 25.
相似三角形的性质
1、相似三角形对应高的比等于相似比.
2、相似三角形的面积比等于相似比的平方
3、相似三角形的周长比等于相似比
4、对应边上的中线的比等于相似比;
对应角上的角平分线的比等于相似比。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
