【原创精品】人教版数学九年级下册 27.3.1 《位似1》课件 (共31张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 27.3.1 《位似1》课件 (共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览





文档简介
(共31张PPT)
27.1.1 图形的相似
人教版九年级下册
第二十七章 相似
1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质;
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
3.培养学生分类讨论问题的能力.
重点:了解并掌握位似图形的定义和性质.
难点:掌握位似变化的方法,运用定义和性质进行简单的位似图形的证明和计算.
学习目标
重点难点
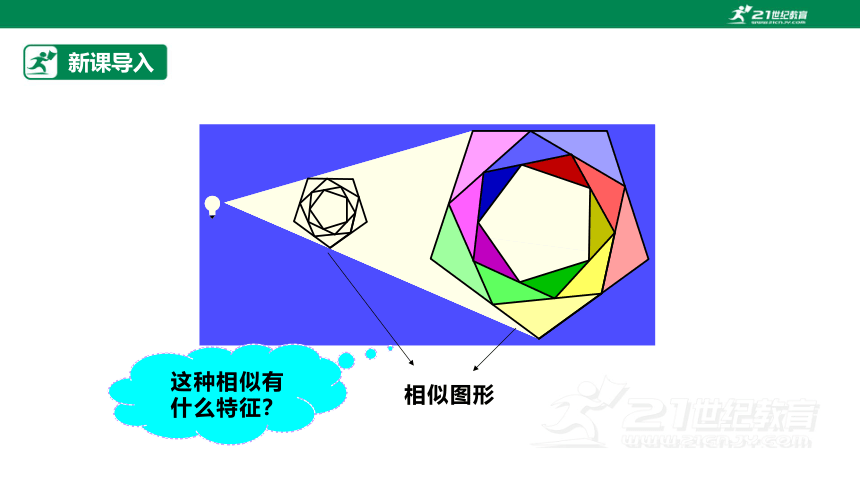
相似图形
这种相似有什么特征?
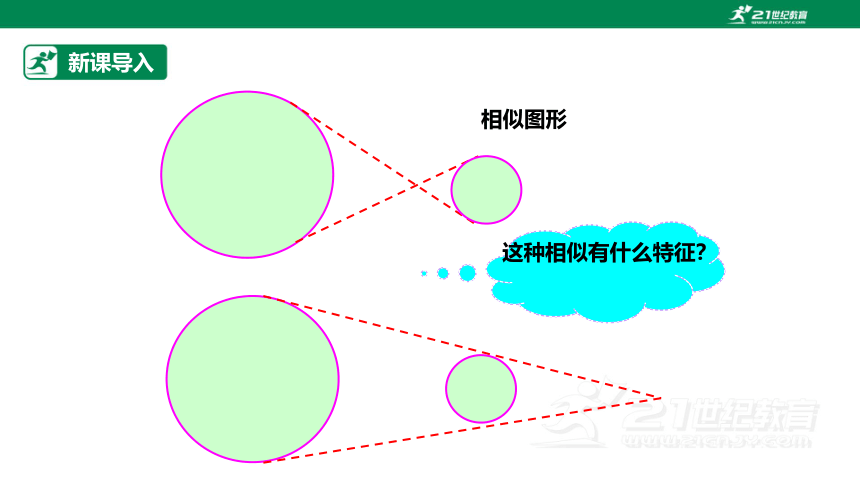
相似图形
这种相似有什么特征?
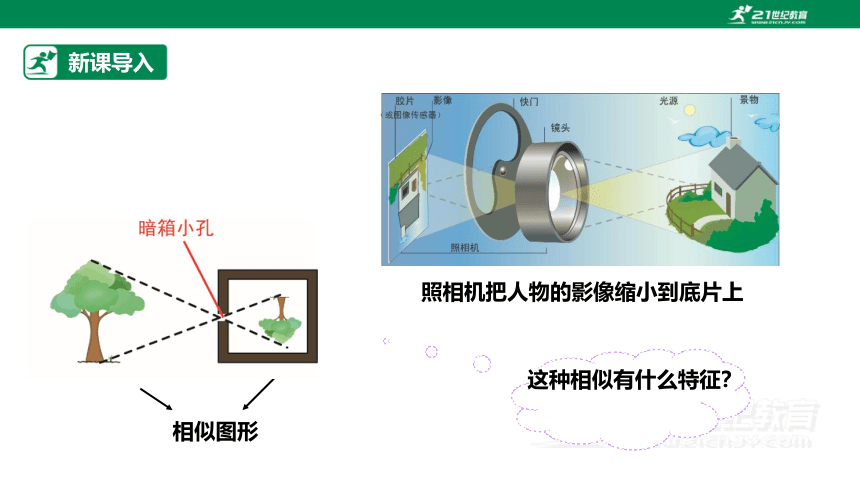
照相机把人物的影像缩小到底片上
相似图形
这种相似有什么特征?
1. 在幻灯机放映图片的过程中,这些图片有什么关系?
2. 幻灯机在哪儿呢?
3.我们能给这种有特殊位置的相似图形一个名称吗?
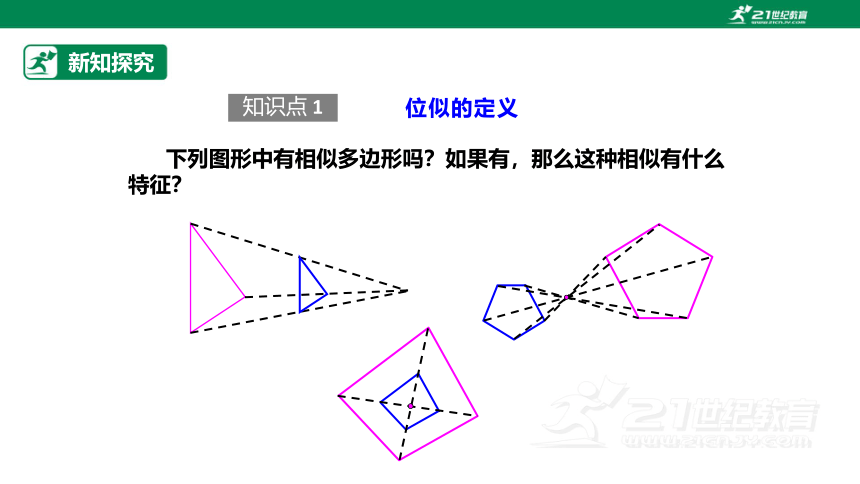
下列图形中有相似多边形吗?如果有,那么这种相似有什么特征?
知识点 1
位似的定义
【讨论】什么样的图形叫做位似图形?什么叫做位似中心? 如何判断两个图形是否位似图形?
两个相似多边形,如果它们对应顶点的连线相交于一点,我们就把这样的两个图形叫做位似图形,这个交点叫做位似
中心.
判断两个图形是不是位似图形,需要从两方面去考察:
(1)这两个图形是否相似;
(2)是否有特殊的位置关系,即每组对应顶点的连线是否都经过同一点.
判定位似图形的方法
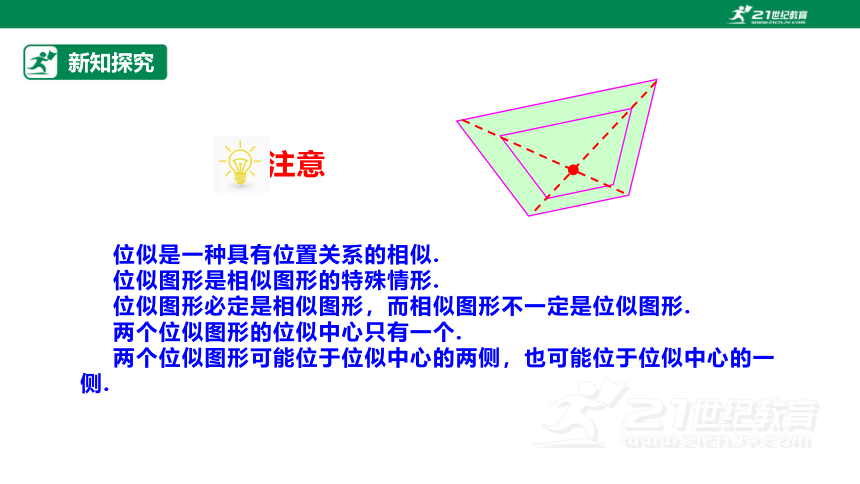
位似是一种具有位置关系的相似.
位似图形是相似图形的特殊情形.
位似图形必定是相似图形,而相似图形不一定是位似图形.
两个位似图形的位似中心只有一个.
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧.
注意
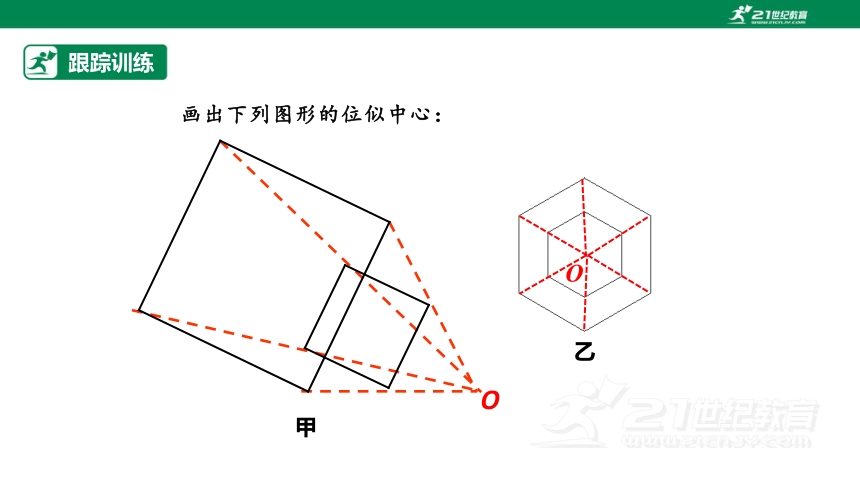
画出下列图形的位似中心:
O
乙
O
甲
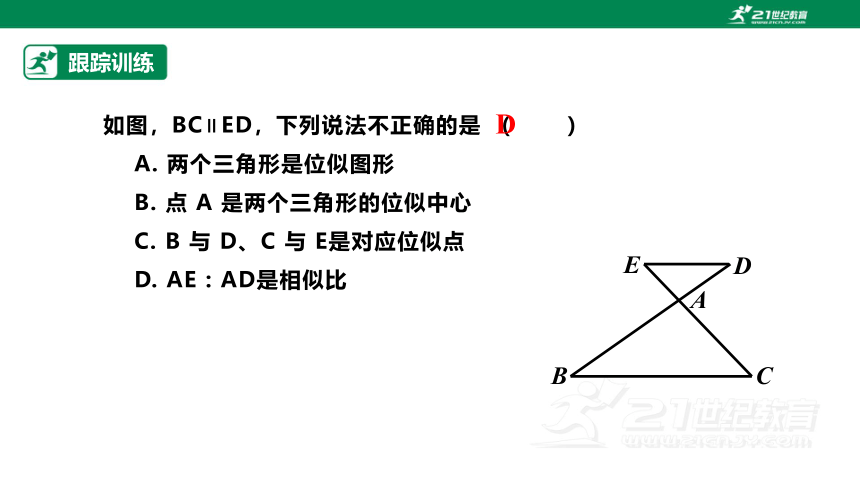
如图,BC∥ED,下列说法不正确的是 ( )
A. 两个三角形是位似图形
B. 点 A 是两个三角形的位似中心
C. B 与 D、C 与 E是对应位似点
D. AE : AD是相似比
D
D
E
A
B
C
从左图中我们可以看到,△OAB∽△OA′B′,
则 ,AB∥A′B′. 右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
知识点 2
位似图形的性质
【总结】位似图形的所有对应点的连线交于一点.位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.位似图形的相似比也叫做位似比,位似图形上任意一对对应点到位似中心的距离之比等于位似比.
【思考】位似图形和相似图形有什么联系和区别?位似图形有何性质?
如图,四边形木框 ABCD 在灯泡发出的光照射下形成的影子是四边形′B′C′D′,若 OB : OB′=1 : 2,则四边形 ABCD 的面积与四边形A′B′C′D′的面积比为 ( )
A.4∶1 B.
C. D.1∶4
D
O
2. 分别在线段OA、OB、OC、OD上取点A'、B'、C'、D',使得
3. 顺次连接点A'、B'、C'、D',所得四边形A'B'C'D'就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
利用位似可以把一个图形放大或缩小.例如,要把四边形ABCD缩小到原来的 ,
1. 在四边形外任选一点O(如图),
知识点 3
位似图形的画法
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点 O,分别在 OA、OB、OC、OD 的反向延长线上取 A′ 、B′ 、C′、D′,使得 呢?如果点 O 取在四边形 ABCD 内部呢?分别画出这时得到的图形.
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
A'
B'
C'
D'
① 确定位似中心;
② 分别连接位似中心和能代表原图的关键点并延长;
③ 根据相似比,确定能代表所作的位似图形的关键点;
④ 顺次连接上述各点,得到放大或缩小的图形.
画位似图形的一般步骤
(1)要弄清位似比,即分清是已知图形与新图形的相似比,还是新图形与原图形的相似比.
(2)若问题没有指定位似中心的位置,则画图时位似中心的取法有多种,对画图而言,以多边形的一个顶点为位似中心画图最简捷.
方法点拨
如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且 ,则 _______.
A
B
C
D
1. 选出下面不同于其他三组的图形 ( )
B
2. 如图,正五边形 FGHMN 与正五边形 ABCDE 是位似图形,若AB : FG = 2 : 3,则下列结论正确的是 ( )
2 DE = 3 MN B. 3DE =2MN
C. 3∠A = 2∠F D. 2∠A = 3∠F
B
A
B
E
C
D
N
F
G
H
M
3.如图,△OAB和△OCD是位似图形,AB与CD平行吗?为什么?
O
A
B
C
D
解:AB∥CD.
∵△OAB与△ODC是位似图形,
∴△OAB∽△OCD.
∴∠OAB=∠C.
∴ AB∥CD.
如图,△ABC. 根据要求作△A'B'C',使△A' B' C'∽△ABC,且相似比为 1 : 5.(1)位似中心在△ABC的一条边AB上;
A
C
B
O
●
A′
B′
C′
●
●
假设位似中心点 O 为 AB中点,点 O 位置如图所示.
根据相似比可确定 A′,B′,C′ 的位置.
●
(2) 以点 C 为位似中心.
C
A
B
A′
B′
( C′ )
●
●
●
如图,F 在 BD 上,BC、AD 相交于点 E,且 AB∥CD∥EF, (1) 图中有哪几对位似三角形 选其中一对加以证明;
答案:△DFE 与 △DBA,△BFE 与 △BDC,△AEB 与 △DEC 都是位似图形;证明略.
(2) 若 AB=2,CD=3,求 EF 的长.
解:∵ △BFE ∽△BDC,△AEB ∽△DEC,
AB=2,CD=3,
∴
∴
解得
位似的概念及画法
位似图形的概念
位似图形的性质
画位似图形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
27.1.1 图形的相似
人教版九年级下册
第二十七章 相似
1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质;
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
3.培养学生分类讨论问题的能力.
重点:了解并掌握位似图形的定义和性质.
难点:掌握位似变化的方法,运用定义和性质进行简单的位似图形的证明和计算.
学习目标
重点难点
相似图形
这种相似有什么特征?
相似图形
这种相似有什么特征?
照相机把人物的影像缩小到底片上
相似图形
这种相似有什么特征?
1. 在幻灯机放映图片的过程中,这些图片有什么关系?
2. 幻灯机在哪儿呢?
3.我们能给这种有特殊位置的相似图形一个名称吗?
下列图形中有相似多边形吗?如果有,那么这种相似有什么特征?
知识点 1
位似的定义
【讨论】什么样的图形叫做位似图形?什么叫做位似中心? 如何判断两个图形是否位似图形?
两个相似多边形,如果它们对应顶点的连线相交于一点,我们就把这样的两个图形叫做位似图形,这个交点叫做位似
中心.
判断两个图形是不是位似图形,需要从两方面去考察:
(1)这两个图形是否相似;
(2)是否有特殊的位置关系,即每组对应顶点的连线是否都经过同一点.
判定位似图形的方法
位似是一种具有位置关系的相似.
位似图形是相似图形的特殊情形.
位似图形必定是相似图形,而相似图形不一定是位似图形.
两个位似图形的位似中心只有一个.
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧.
注意
画出下列图形的位似中心:
O
乙
O
甲
如图,BC∥ED,下列说法不正确的是 ( )
A. 两个三角形是位似图形
B. 点 A 是两个三角形的位似中心
C. B 与 D、C 与 E是对应位似点
D. AE : AD是相似比
D
D
E
A
B
C
从左图中我们可以看到,△OAB∽△OA′B′,
则 ,AB∥A′B′. 右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
知识点 2
位似图形的性质
【总结】位似图形的所有对应点的连线交于一点.位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.位似图形的相似比也叫做位似比,位似图形上任意一对对应点到位似中心的距离之比等于位似比.
【思考】位似图形和相似图形有什么联系和区别?位似图形有何性质?
如图,四边形木框 ABCD 在灯泡发出的光照射下形成的影子是四边形′B′C′D′,若 OB : OB′=1 : 2,则四边形 ABCD 的面积与四边形A′B′C′D′的面积比为 ( )
A.4∶1 B.
C. D.1∶4
D
O
2. 分别在线段OA、OB、OC、OD上取点A'、B'、C'、D',使得
3. 顺次连接点A'、B'、C'、D',所得四边形A'B'C'D'就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
利用位似可以把一个图形放大或缩小.例如,要把四边形ABCD缩小到原来的 ,
1. 在四边形外任选一点O(如图),
知识点 3
位似图形的画法
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点 O,分别在 OA、OB、OC、OD 的反向延长线上取 A′ 、B′ 、C′、D′,使得 呢?如果点 O 取在四边形 ABCD 内部呢?分别画出这时得到的图形.
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
A'
B'
C'
D'
① 确定位似中心;
② 分别连接位似中心和能代表原图的关键点并延长;
③ 根据相似比,确定能代表所作的位似图形的关键点;
④ 顺次连接上述各点,得到放大或缩小的图形.
画位似图形的一般步骤
(1)要弄清位似比,即分清是已知图形与新图形的相似比,还是新图形与原图形的相似比.
(2)若问题没有指定位似中心的位置,则画图时位似中心的取法有多种,对画图而言,以多边形的一个顶点为位似中心画图最简捷.
方法点拨
如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且 ,则 _______.
A
B
C
D
1. 选出下面不同于其他三组的图形 ( )
B
2. 如图,正五边形 FGHMN 与正五边形 ABCDE 是位似图形,若AB : FG = 2 : 3,则下列结论正确的是 ( )
2 DE = 3 MN B. 3DE =2MN
C. 3∠A = 2∠F D. 2∠A = 3∠F
B
A
B
E
C
D
N
F
G
H
M
3.如图,△OAB和△OCD是位似图形,AB与CD平行吗?为什么?
O
A
B
C
D
解:AB∥CD.
∵△OAB与△ODC是位似图形,
∴△OAB∽△OCD.
∴∠OAB=∠C.
∴ AB∥CD.
如图,△ABC. 根据要求作△A'B'C',使△A' B' C'∽△ABC,且相似比为 1 : 5.(1)位似中心在△ABC的一条边AB上;
A
C
B
O
●
A′
B′
C′
●
●
假设位似中心点 O 为 AB中点,点 O 位置如图所示.
根据相似比可确定 A′,B′,C′ 的位置.
●
(2) 以点 C 为位似中心.
C
A
B
A′
B′
( C′ )
●
●
●
如图,F 在 BD 上,BC、AD 相交于点 E,且 AB∥CD∥EF, (1) 图中有哪几对位似三角形 选其中一对加以证明;
答案:△DFE 与 △DBA,△BFE 与 △BDC,△AEB 与 △DEC 都是位似图形;证明略.
(2) 若 AB=2,CD=3,求 EF 的长.
解:∵ △BFE ∽△BDC,△AEB ∽△DEC,
AB=2,CD=3,
∴
∴
解得
位似的概念及画法
位似图形的概念
位似图形的性质
画位似图形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
