【原创精品】人教版数学九年级下册 27.3.2 《位似2》课件 (共26张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 27.3.2 《位似2》课件 (共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览






文档简介
(共26张PPT)
27.1.1 图形的相似
人教版九年级下册
第二十七章 相似
1.理解位似变换与坐标变换.
2.掌握在直角坐标系中的位似变换.
3.熟练根据相似比求与一个多边形位似的多边形的顶点坐标.
重点:用图形的坐标的变化来表示图形的位似变换.
难点:把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律.
学习目标
重点难点
1.什么是位似图形
2.如何判断两个图形是否位似
3.怎样求两个位似图形的相似比
4.如何将画在纸上的一个图形放大,使放大前后对应线段的比为1: 2 你有哪些方法
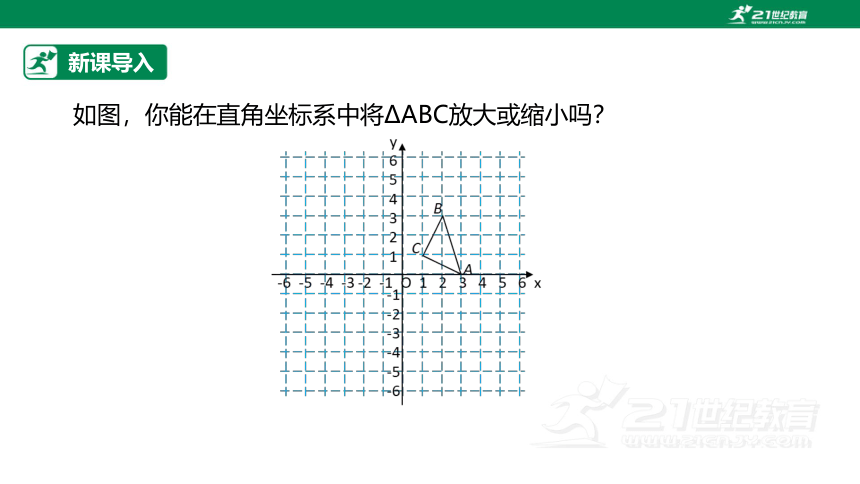
如图,你能在直角坐标系中将 ABC放大或缩小吗?
1.位似多边形的坐标变化规律
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(3,0)、B(2,3)、C (1,1),将点A、B、C的横坐标、纵坐标都乘2,得到三个点A (___,___)、B (___,___)、C (___,___), A B C 与△ABC是否位似_____.如果位似,指出位似中心是_________和相似比是___.
6 0
A
4 6
B
2 2
C
是
(0,0)
2
1.位似多边形的坐标变化规律
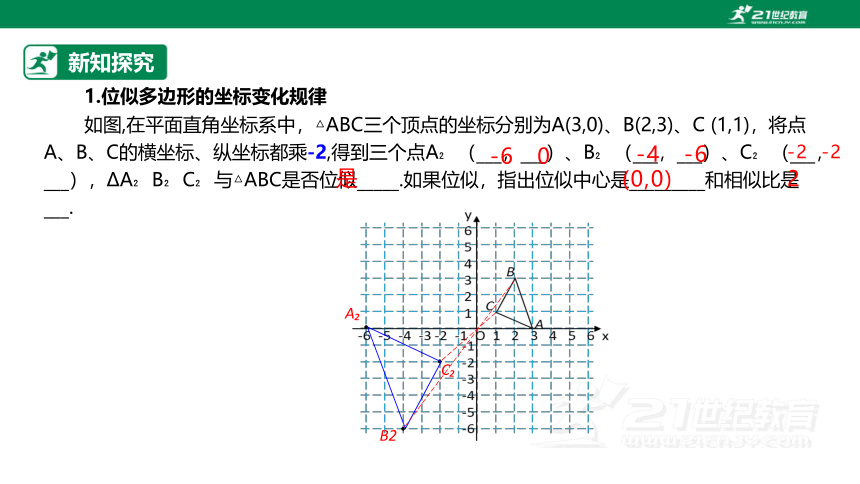
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(3,0)、B(2,3)、C (1,1),将点A、B、C的横坐标、纵坐标都乘-2,得到三个点A (___,___)、B (___,___)、C (___,___), A B C 与△ABC是否位似_____.如果位似,指出位似中心是_________和相似比是___.
-6 0
A
-4 -6
B2
-2 -2
C
是
(0,0)
2
归纳
(1)在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k(k≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比为|k|.
(2)当位似图形在原点同侧时,其对应顶点的坐标的比为k(k>0);当位似图形在原点两侧时,其对应顶点的坐标的比为-k(k>0).
(3)当|k|>1时,图形扩大为原来的|k|倍:当0<|k<1时,图形缩小为原来的|k|.
注意
这里的相似比是新图形与原图形的对应边的相似比.
2.位似变换与平移、轴对称旋转三种变换的联系和区别:
位似、平移、轴对称、旋转都是图形变换的基本形式,它们的本质区别在于:平移、轴对称、旋转三种图形变换是全等变换,而位似变换是相似变换,在直角坐标系中,把一个图形进行平移、轴对称、旋转和位似变换,其对应点的坐标都有各自的变化规律:
(1)平移变换是横坐标或纵坐标加上(或减去)平移的距离;
(2)轴对称变换,以x轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数;
(3)在旋转变换中,一个图形绕原点旋转180°,则旋转前后两个图形对应点的横坐标与纵坐标都分别互为相反数;
(4)位似变换中,当以原点为位似中心时,变换后与变换前两个图形对应点的横坐标之比的绝对值、纵坐标之比的绝对值都等于相似比.
1. 位似图形的坐标变化规律
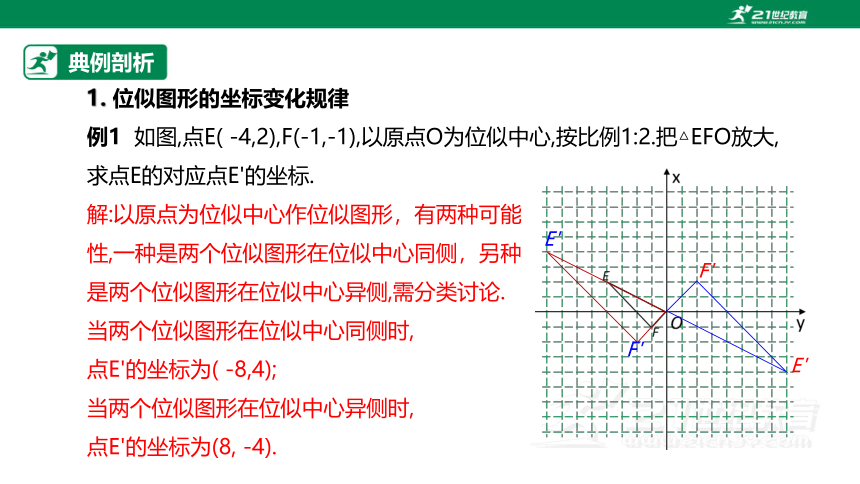
例1 如图,点E( -4,2),F(-1,-1),以原点O为位似中心,按比例1:2.把△EFO放大,
求点E的对应点E'的坐标.
解:以原点为位似中心作位似图形,有两种可能
性,一种是两个位似图形在位似中心同侧,另种
是两个位似图形在位似中心异侧,需分类讨论.
当两个位似图形在位似中心同侧时,
点E'的坐标为( -8,4);
当两个位似图形在位似中心异侧时,
点E'的坐标为(8, -4).
F'
E'
E'
F'
原点为位似中心的坐标规律
平面直角坐标系中,如果位似变化是以原点为住似中心,相似比为k(k>0),那么位似图形对应点的坐标的比等于k或-k,一般有两种情况若原图形中一点的坐标为(x ,y ),则其对应点的坐标为(kx ,ky )或( -kx , -ky ).
如图,在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(2,0),B(2,1) ,C(0,1),以坐标原点O为位似中心,将矩形OABC放大为原图形的2倍,记所得矩形为OA B C 点B的对应点为B ,且B 在OB的延长线上,则点B 的坐标为_____.
(4,2)
2.平面直角坐标系中的位似作图
例2 将图的OABC分别做下列变化,指出三个顶点的坐标所发生的变化
(1)沿x轴正向平移2个单位长度;
(2)关于x轴对称;
(3)以B点为位似中心,放大到原来的2倍(在B点同侧) ,画出相应的图形.
分析:△ABC沿x轴正向平移2个单位长度,所有点的纵坐标不变,横坐标增加2个单位长度;
图形关于x轴对称,横坐标不变,纵坐标变为原来的相反数;
以B点为位似中心则B点的对应点仍是B点.
例2 将图的OABC分别做下列变化,指出三个顶点的坐标所发生的变化
(1)沿x轴正向平移2个单位长度;
(2)关于x轴对称;
(3)以B点为位似中心,放大到原来的2倍(在B点同侧) ,画出相应的图形.
解:△ABC的三个顶点的坐标分别为A(0, -2) ,B(3,-1),C(2,1).
(1)沿x 轴正向平移2个单位长度之后的 A B C 的对应顶
点分别是A (2, -2),B (5.-1),C (4,1).
(2) 关于x轴对称的 A B C 的对应顶点分别是A (0,2),
B (3,1),C(2,-1).
(3)以B点为位似中心,放大到原来的2倍的 A BC 的对应
顶点坐标分别为A ( -3, -3),B(3,-1),C (1,3).
A
B
C
A
B
C
A
C
图形在平面直角坐标系中的变换,其中平移变换、对称(轴对称与中心对称)变换属于全等变换,只有相似变换可以将图形放大或缩小.若图形与原图形的相似比为k(k>0),当k>1时,图形扩大;当0相似比与图形扩大缩小的关系
如图, ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是1个单位长度).
(1)画出 ABC向下平移4个单位长度得到的 A B C ,点C 的坐标是_______;
(2)以点B为位似中心,在网格内画出 A B C ,使△A B C 与 ABC位似(在点B同侧),且相似比为2:1.点C 的坐标是_________ ;
(3) A B C 的面积是_______ 平方单位长度.
x
y
A
B
O
C
A
B
C
(2,-2)
A
C
B
(1,0)
10
如图,在平面直角坐标系中,点A,B的坐标分别为(3,2),(6,4),AC⊥x轴于点C,BG ⊥x轴于点G,分别以AC,BG为边作正方形ACDE和正方形BGMN.
(1)试分别写出直线AB和直线EN对应的函数表达式;
(2)求证:正方形ACDE和正方形BGMN是位似图形;
(3)已知点M的坐标是(10,0),试作一个正方形,它以点M为其中一个顶点,且与已有正方形成位似图形(在下图中作出即可).
解:(1)设直线AB的解析式为y=kx+b(k≠0),
将A(3,2),B(6,4)代入得:3k+b=2,6k+b=4
解得:k=2/3,b=0
∴直线AB的解析式为:y= x
同理可以计算出直线EN的解析式为:y=2/5 x
如图,在平面直角坐标系中,点A,B的坐标分别为(3,2),(6,4),AC⊥x轴于点C,BG ⊥x轴于点G,分别以AC,BG为边作正方形ACDE和正方形BGMN.
(1)试分别写出直线AB和直线EN对应的函数表达式;
(2)求证:正方形ACDE和正方形BGMN是位似图形;
(3)已知点M的坐标是(10,0),试作一个正方形,它以点M为其中一个顶点,且与已有正方形成位似图形(在下图中作出即可).
解:(2)∵直线AB解析式为y= x与直线NE解析式
为y=2/5 x都过原点,直线DM与直线CG都与x轴重合,
∴正方形ACDE与正方形BGMN对应顶点连线交于一点,
此点为原点,则正方形ACDE和正方形BGMN是位似图形;
如图,在平面直角坐标系中,点A,B的坐标分别为(3,2),(6,4),AC⊥x轴于点C,BG ⊥x轴于点G,分别以AC,BG为边作正方形ACDE和正方形BGMN.
(1)试分别写出直线AB和直线EN对应的函数表达式;
(2)求证:正方形ACDE和正方形BGMN是位似图形;
(3)已知点M的坐标是(10,0),试作一个正方形,它以点M为其中一个顶点,且与已有正方形成位似图形(在下图中作出即可).
解:(3)如图所示,正方形MN′B′G′,
正方形A′E′D′C′为所求的正方形.
A
如图,线段CD两个端点的坐标分别为C(﹣1,﹣2),D(﹣2,﹣1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的2倍,得到线段AB,则线段AB的中点E的坐标为( )
A.(3,3) B.( , )
C.(2,4) D.(4,2)
1.在平面直角坐标系中,有两点A(4,2),B(3,0),以原点为位似中心,把AB缩小为原来的1/2,得到线段A'B'.正确的画法是( )
D
2.如图,已知△ABO与△DCO位似,且△ABO与△DCO的面积之比为1∶4,点B的坐标为(-3,2),则点C的坐标为( )
A.(3,-2) B.(6,-4)
C.(4,-6) D.(6,4)
3.如图,在平面直角坐标系xOy中,有两点A(2,4),B(4,0),以原点O为位似中心,把△OAB缩小得到△OA'B'.若点B'的坐标为(2,0),则点A'的坐标为_________.
B
(1,2)
4.如图,已知矩形OABC与矩形ODEF是位似图形,点P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为______.
(-2,0)
5.如图,在平面直角坐标系中,△ABC和△A'B'C'是以坐标原点O为位似中心的位似图形,且点B(3,1),B'(6,2).
(1)请你根据位似的特征并结合点B与点B'的坐标回答下列问题:
①若点A(5/2 ,3 ),则点A'的坐标为________;
②△ABC与△A'B'C'的相似比为____________;
(2)若△ABC的面积为m,求△A'B'C'的面积.(用含m的代数式表示)
解: (1)①∵点B(3,1),B'(6,2),∴△A'B'C'与△ABC的相似比为2,又点A的坐标为(5/2 ,3 ),
∴点A'的坐标为(5,6).
②△ABC与△A'B'C'的相似比为1∶2.
(2)∵△ABC与△A'B'C'的相似比为1∶2,∴S△ABC/S△A'B' C' ) =1/4,
又∵△ABC的面积为m,∴△A'B'C'的面积为4m.
(5/2 ,3 )
(5/2 ,3(5,6)
图形的位似
位似作图
位似变换
点(a,b)以原点为位似中心,k为相似比,
对应顶点的坐标为(ka,kb)或(-ka,-kb)
关键是确定好位似中心,相似比和关键点的对应点
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
27.1.1 图形的相似
人教版九年级下册
第二十七章 相似
1.理解位似变换与坐标变换.
2.掌握在直角坐标系中的位似变换.
3.熟练根据相似比求与一个多边形位似的多边形的顶点坐标.
重点:用图形的坐标的变化来表示图形的位似变换.
难点:把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律.
学习目标
重点难点
1.什么是位似图形
2.如何判断两个图形是否位似
3.怎样求两个位似图形的相似比
4.如何将画在纸上的一个图形放大,使放大前后对应线段的比为1: 2 你有哪些方法
如图,你能在直角坐标系中将 ABC放大或缩小吗?
1.位似多边形的坐标变化规律
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(3,0)、B(2,3)、C (1,1),将点A、B、C的横坐标、纵坐标都乘2,得到三个点A (___,___)、B (___,___)、C (___,___), A B C 与△ABC是否位似_____.如果位似,指出位似中心是_________和相似比是___.
6 0
A
4 6
B
2 2
C
是
(0,0)
2
1.位似多边形的坐标变化规律
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(3,0)、B(2,3)、C (1,1),将点A、B、C的横坐标、纵坐标都乘-2,得到三个点A (___,___)、B (___,___)、C (___,___), A B C 与△ABC是否位似_____.如果位似,指出位似中心是_________和相似比是___.
-6 0
A
-4 -6
B2
-2 -2
C
是
(0,0)
2
归纳
(1)在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k(k≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比为|k|.
(2)当位似图形在原点同侧时,其对应顶点的坐标的比为k(k>0);当位似图形在原点两侧时,其对应顶点的坐标的比为-k(k>0).
(3)当|k|>1时,图形扩大为原来的|k|倍:当0<|k<1时,图形缩小为原来的|k|.
注意
这里的相似比是新图形与原图形的对应边的相似比.
2.位似变换与平移、轴对称旋转三种变换的联系和区别:
位似、平移、轴对称、旋转都是图形变换的基本形式,它们的本质区别在于:平移、轴对称、旋转三种图形变换是全等变换,而位似变换是相似变换,在直角坐标系中,把一个图形进行平移、轴对称、旋转和位似变换,其对应点的坐标都有各自的变化规律:
(1)平移变换是横坐标或纵坐标加上(或减去)平移的距离;
(2)轴对称变换,以x轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数;
(3)在旋转变换中,一个图形绕原点旋转180°,则旋转前后两个图形对应点的横坐标与纵坐标都分别互为相反数;
(4)位似变换中,当以原点为位似中心时,变换后与变换前两个图形对应点的横坐标之比的绝对值、纵坐标之比的绝对值都等于相似比.
1. 位似图形的坐标变化规律
例1 如图,点E( -4,2),F(-1,-1),以原点O为位似中心,按比例1:2.把△EFO放大,
求点E的对应点E'的坐标.
解:以原点为位似中心作位似图形,有两种可能
性,一种是两个位似图形在位似中心同侧,另种
是两个位似图形在位似中心异侧,需分类讨论.
当两个位似图形在位似中心同侧时,
点E'的坐标为( -8,4);
当两个位似图形在位似中心异侧时,
点E'的坐标为(8, -4).
F'
E'
E'
F'
原点为位似中心的坐标规律
平面直角坐标系中,如果位似变化是以原点为住似中心,相似比为k(k>0),那么位似图形对应点的坐标的比等于k或-k,一般有两种情况若原图形中一点的坐标为(x ,y ),则其对应点的坐标为(kx ,ky )或( -kx , -ky ).
如图,在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(2,0),B(2,1) ,C(0,1),以坐标原点O为位似中心,将矩形OABC放大为原图形的2倍,记所得矩形为OA B C 点B的对应点为B ,且B 在OB的延长线上,则点B 的坐标为_____.
(4,2)
2.平面直角坐标系中的位似作图
例2 将图的OABC分别做下列变化,指出三个顶点的坐标所发生的变化
(1)沿x轴正向平移2个单位长度;
(2)关于x轴对称;
(3)以B点为位似中心,放大到原来的2倍(在B点同侧) ,画出相应的图形.
分析:△ABC沿x轴正向平移2个单位长度,所有点的纵坐标不变,横坐标增加2个单位长度;
图形关于x轴对称,横坐标不变,纵坐标变为原来的相反数;
以B点为位似中心则B点的对应点仍是B点.
例2 将图的OABC分别做下列变化,指出三个顶点的坐标所发生的变化
(1)沿x轴正向平移2个单位长度;
(2)关于x轴对称;
(3)以B点为位似中心,放大到原来的2倍(在B点同侧) ,画出相应的图形.
解:△ABC的三个顶点的坐标分别为A(0, -2) ,B(3,-1),C(2,1).
(1)沿x 轴正向平移2个单位长度之后的 A B C 的对应顶
点分别是A (2, -2),B (5.-1),C (4,1).
(2) 关于x轴对称的 A B C 的对应顶点分别是A (0,2),
B (3,1),C(2,-1).
(3)以B点为位似中心,放大到原来的2倍的 A BC 的对应
顶点坐标分别为A ( -3, -3),B(3,-1),C (1,3).
A
B
C
A
B
C
A
C
图形在平面直角坐标系中的变换,其中平移变换、对称(轴对称与中心对称)变换属于全等变换,只有相似变换可以将图形放大或缩小.若图形与原图形的相似比为k(k>0),当k>1时,图形扩大;当0
如图, ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是1个单位长度).
(1)画出 ABC向下平移4个单位长度得到的 A B C ,点C 的坐标是_______;
(2)以点B为位似中心,在网格内画出 A B C ,使△A B C 与 ABC位似(在点B同侧),且相似比为2:1.点C 的坐标是_________ ;
(3) A B C 的面积是_______ 平方单位长度.
x
y
A
B
O
C
A
B
C
(2,-2)
A
C
B
(1,0)
10
如图,在平面直角坐标系中,点A,B的坐标分别为(3,2),(6,4),AC⊥x轴于点C,BG ⊥x轴于点G,分别以AC,BG为边作正方形ACDE和正方形BGMN.
(1)试分别写出直线AB和直线EN对应的函数表达式;
(2)求证:正方形ACDE和正方形BGMN是位似图形;
(3)已知点M的坐标是(10,0),试作一个正方形,它以点M为其中一个顶点,且与已有正方形成位似图形(在下图中作出即可).
解:(1)设直线AB的解析式为y=kx+b(k≠0),
将A(3,2),B(6,4)代入得:3k+b=2,6k+b=4
解得:k=2/3,b=0
∴直线AB的解析式为:y= x
同理可以计算出直线EN的解析式为:y=2/5 x
如图,在平面直角坐标系中,点A,B的坐标分别为(3,2),(6,4),AC⊥x轴于点C,BG ⊥x轴于点G,分别以AC,BG为边作正方形ACDE和正方形BGMN.
(1)试分别写出直线AB和直线EN对应的函数表达式;
(2)求证:正方形ACDE和正方形BGMN是位似图形;
(3)已知点M的坐标是(10,0),试作一个正方形,它以点M为其中一个顶点,且与已有正方形成位似图形(在下图中作出即可).
解:(2)∵直线AB解析式为y= x与直线NE解析式
为y=2/5 x都过原点,直线DM与直线CG都与x轴重合,
∴正方形ACDE与正方形BGMN对应顶点连线交于一点,
此点为原点,则正方形ACDE和正方形BGMN是位似图形;
如图,在平面直角坐标系中,点A,B的坐标分别为(3,2),(6,4),AC⊥x轴于点C,BG ⊥x轴于点G,分别以AC,BG为边作正方形ACDE和正方形BGMN.
(1)试分别写出直线AB和直线EN对应的函数表达式;
(2)求证:正方形ACDE和正方形BGMN是位似图形;
(3)已知点M的坐标是(10,0),试作一个正方形,它以点M为其中一个顶点,且与已有正方形成位似图形(在下图中作出即可).
解:(3)如图所示,正方形MN′B′G′,
正方形A′E′D′C′为所求的正方形.
A
如图,线段CD两个端点的坐标分别为C(﹣1,﹣2),D(﹣2,﹣1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的2倍,得到线段AB,则线段AB的中点E的坐标为( )
A.(3,3) B.( , )
C.(2,4) D.(4,2)
1.在平面直角坐标系中,有两点A(4,2),B(3,0),以原点为位似中心,把AB缩小为原来的1/2,得到线段A'B'.正确的画法是( )
D
2.如图,已知△ABO与△DCO位似,且△ABO与△DCO的面积之比为1∶4,点B的坐标为(-3,2),则点C的坐标为( )
A.(3,-2) B.(6,-4)
C.(4,-6) D.(6,4)
3.如图,在平面直角坐标系xOy中,有两点A(2,4),B(4,0),以原点O为位似中心,把△OAB缩小得到△OA'B'.若点B'的坐标为(2,0),则点A'的坐标为_________.
B
(1,2)
4.如图,已知矩形OABC与矩形ODEF是位似图形,点P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为______.
(-2,0)
5.如图,在平面直角坐标系中,△ABC和△A'B'C'是以坐标原点O为位似中心的位似图形,且点B(3,1),B'(6,2).
(1)请你根据位似的特征并结合点B与点B'的坐标回答下列问题:
①若点A(5/2 ,3 ),则点A'的坐标为________;
②△ABC与△A'B'C'的相似比为____________;
(2)若△ABC的面积为m,求△A'B'C'的面积.(用含m的代数式表示)
解: (1)①∵点B(3,1),B'(6,2),∴△A'B'C'与△ABC的相似比为2,又点A的坐标为(5/2 ,3 ),
∴点A'的坐标为(5,6).
②△ABC与△A'B'C'的相似比为1∶2.
(2)∵△ABC与△A'B'C'的相似比为1∶2,∴S△ABC/S△A'B' C' ) =1/4,
又∵△ABC的面积为m,∴△A'B'C'的面积为4m.
(5/2 ,3 )
(5/2 ,3(5,6)
图形的位似
位似作图
位似变换
点(a,b)以原点为位似中心,k为相似比,
对应顶点的坐标为(ka,kb)或(-ka,-kb)
关键是确定好位似中心,相似比和关键点的对应点
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
