【原创精品】人教版数学九年级下册 28.1.1 《正弦函数和余弦函数》课件 (共21张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 28.1.1 《正弦函数和余弦函数》课件 (共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览





文档简介
(共21张PPT)
28.1.1 正弦函数和余弦函数
人教版九年级下册
第二十八章 锐角三角函数
1.掌握三角函数边与角的对应关系;
2.探索正弦、余弦、概念的过程,掌握运用sin A,cos A表示直角边的比;
3.培养学生良好的数形结合的能力,激发学生的求知欲和学 习的自信心.
重点:学会运用正弦、余弦、正切的概念解决实际问题.
难点:学会运用正弦、余弦、正切的概念解决实际问题.
学习目标
重点难点
“神舟”十号载人飞船与“天宫”一号成功实现手控交会对接,对接成功后,将增进人类对太空的了解,解开天宫的神秘面纱.其实,在“神舟十号”发射和对接的过程中,三角函数的测量伴随着航天活动的始终,今天我们就来揭开锐角三角函数的面纱吧!
上一节,我们曾经使用两种方法求出操场旗杆的高度,其中都出现了两个相似的
直角三角形,即△ABC∽△A`B`C`.按 的比例,就一定有:
∴根据比例的性质可以得到:
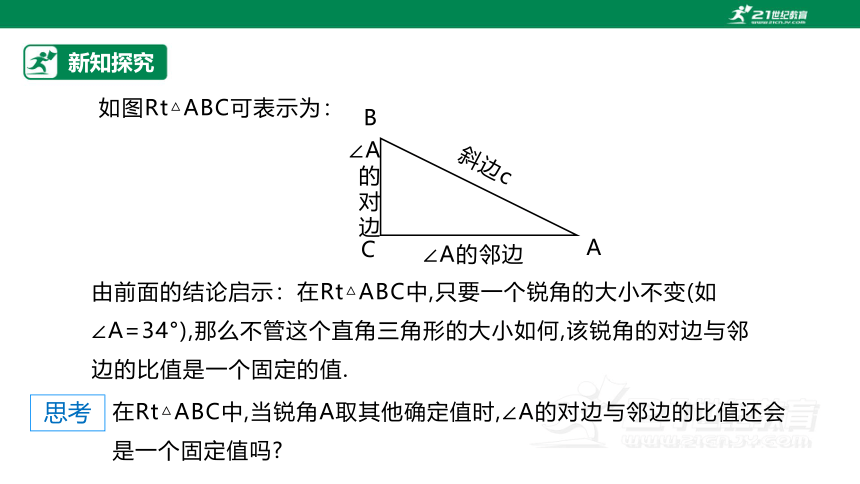
如图Rt△ABC可表示为:
A
B
C
斜边c
∠A的邻边
∠A
的
对
边
由前面的结论启示:在Rt△ABC中,只要一个锐角的大小不变(如∠A=34°),那么不管这个直角三角形的大小如何,该锐角的对边与邻边的比值是一个固定的值.
思考
在Rt△ABC中,当锐角A取其他确定值时,∠A的对边与邻边的比值还会是一个固定值吗
A
C1
C2
C3
B1
B2
B3
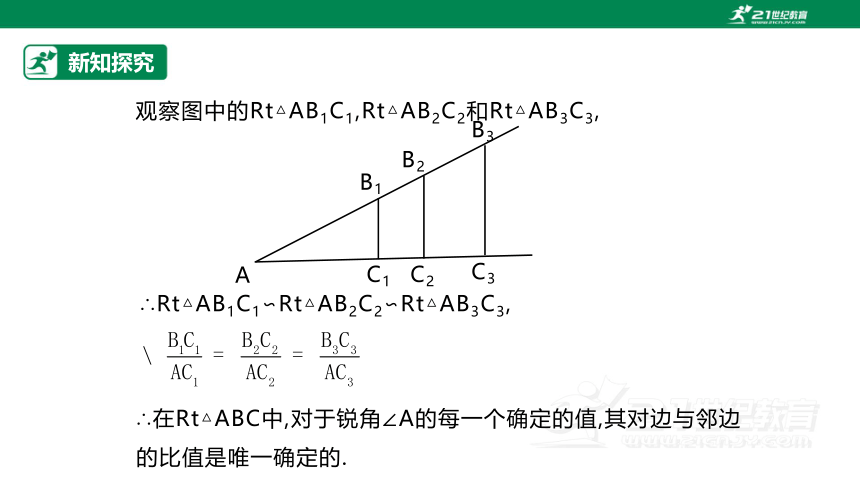
观察图中的Rt△AB1C1,Rt△AB2C2和Rt△AB3C3,
∴Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3,
∴在Rt△ABC中,对于锐角∠A的每一个确定的值,其对边与邻边的比值是唯一确定的.
A
C1
C2
C3
B1
B2
B3
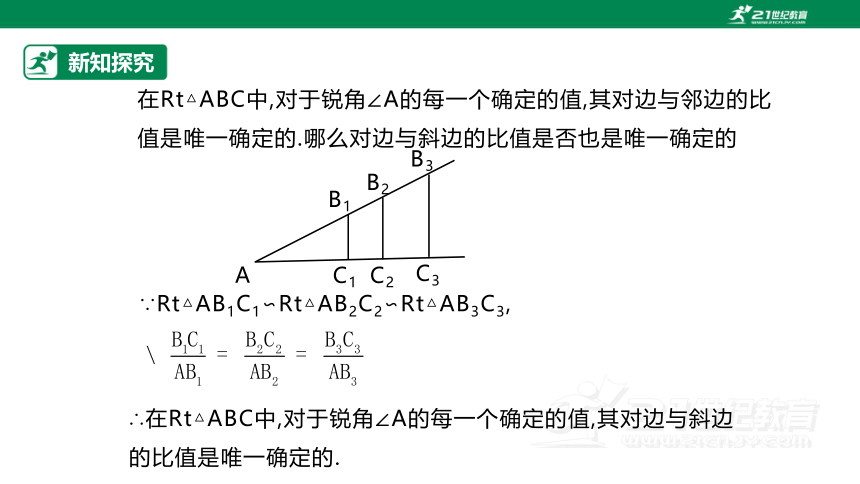
∵Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3,
∴在Rt△ABC中,对于锐角∠A的每一个确定的值,其对边与斜边的比值是唯一确定的.
在Rt△ABC中,对于锐角∠A的每一个确定的值,其对边与邻边的比值是唯一确定的.哪么对边与斜边的比值是否也是唯一确定的
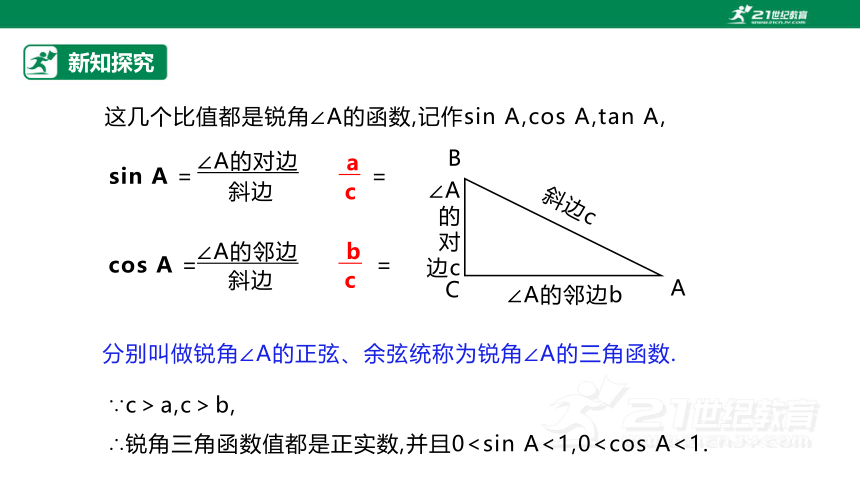
分别叫做锐角∠A的正弦、余弦统称为锐角∠A的三角函数.
这几个比值都是锐角∠A的函数,记作sin A,cos A,tan A,
A
B
C
斜边c
∠A的邻边b
∠A
的
对
边c
∠A的对边
斜边
sin A = =
c
a
∠A的邻边
斜边
cos A = =
c
b
∵c>a,c>b,
∴锐角三角函数值都是正实数,并且0∴锐角三角函数公式:
2. 锐角三角函数公式:
1. 0锐角三角函数的性质
如图,在Rt△ABC中,∠C=90°,AC=15,BC=8,
试求出∠A的正弦和余弦.
8
A
C
B
15
如图,在△ABC中,∠C=90°,sinA= ,AC=9,
求△ABC的周长和cosA的值.
A
C
B
解:在Rt△ABC中,sinA=
设BC=4k,AB=5k(k>0).
由勾股定理可得:(4k)2+92=(5k)2.
∴k=3.
∴BC=12,AB=15.
∴AB+BC+AC=36.
cosA=
小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.994 5,
sin222°+sin268°≈0.372+0.932=1.001 8,
sin229°+sin261°≈0.482+0.872=0.987 3,
sin237°+sin253°≈0.602+0.802=1.000 0,
sin245°+sin245°=( )2+( )2=1.
据此,小明猜想:
对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(1)当α=30°时,验证sin2α+sin2(90°-α)=1是否成立.
(2)小明的猜想是否成立 若成立,请给予证明;若不成立,请举出一个反例.
(中考·乐山) 如图1,已知△ABC的三个顶点均在格点上,则cosA的值为( )
【解析】 D 如图,过点B 作BD⊥AC (点D正好在格点外),如图2,由勾股定理,得AB= ,AD= 所以cosA=
D
1.如图,在4×4的正方形方格中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正弦值是 .
2.在Rt△ABC中,∠C=90°,CD是斜边AB上的高,如果CD=3,BD=2,那么cos A的值是 .
D
A. 4 B. 6 C. 8 D. 10
2
3. 在Rt△ABC中,∠C=90°, ,BC=6,则 AB的长为 ( )
4. 在△ABC 中,∠C=90°,如果 ,AB=6,那么BC=_____.
锐角三角函数
定义:sinA,cosA
0性质
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
28.1.1 正弦函数和余弦函数
人教版九年级下册
第二十八章 锐角三角函数
1.掌握三角函数边与角的对应关系;
2.探索正弦、余弦、概念的过程,掌握运用sin A,cos A表示直角边的比;
3.培养学生良好的数形结合的能力,激发学生的求知欲和学 习的自信心.
重点:学会运用正弦、余弦、正切的概念解决实际问题.
难点:学会运用正弦、余弦、正切的概念解决实际问题.
学习目标
重点难点
“神舟”十号载人飞船与“天宫”一号成功实现手控交会对接,对接成功后,将增进人类对太空的了解,解开天宫的神秘面纱.其实,在“神舟十号”发射和对接的过程中,三角函数的测量伴随着航天活动的始终,今天我们就来揭开锐角三角函数的面纱吧!
上一节,我们曾经使用两种方法求出操场旗杆的高度,其中都出现了两个相似的
直角三角形,即△ABC∽△A`B`C`.按 的比例,就一定有:
∴根据比例的性质可以得到:
如图Rt△ABC可表示为:
A
B
C
斜边c
∠A的邻边
∠A
的
对
边
由前面的结论启示:在Rt△ABC中,只要一个锐角的大小不变(如∠A=34°),那么不管这个直角三角形的大小如何,该锐角的对边与邻边的比值是一个固定的值.
思考
在Rt△ABC中,当锐角A取其他确定值时,∠A的对边与邻边的比值还会是一个固定值吗
A
C1
C2
C3
B1
B2
B3
观察图中的Rt△AB1C1,Rt△AB2C2和Rt△AB3C3,
∴Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3,
∴在Rt△ABC中,对于锐角∠A的每一个确定的值,其对边与邻边的比值是唯一确定的.
A
C1
C2
C3
B1
B2
B3
∵Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3,
∴在Rt△ABC中,对于锐角∠A的每一个确定的值,其对边与斜边的比值是唯一确定的.
在Rt△ABC中,对于锐角∠A的每一个确定的值,其对边与邻边的比值是唯一确定的.哪么对边与斜边的比值是否也是唯一确定的
分别叫做锐角∠A的正弦、余弦统称为锐角∠A的三角函数.
这几个比值都是锐角∠A的函数,记作sin A,cos A,tan A,
A
B
C
斜边c
∠A的邻边b
∠A
的
对
边c
∠A的对边
斜边
sin A = =
c
a
∠A的邻边
斜边
cos A = =
c
b
∵c>a,c>b,
∴锐角三角函数值都是正实数,并且0
2. 锐角三角函数公式:
1. 0
如图,在Rt△ABC中,∠C=90°,AC=15,BC=8,
试求出∠A的正弦和余弦.
8
A
C
B
15
如图,在△ABC中,∠C=90°,sinA= ,AC=9,
求△ABC的周长和cosA的值.
A
C
B
解:在Rt△ABC中,sinA=
设BC=4k,AB=5k(k>0).
由勾股定理可得:(4k)2+92=(5k)2.
∴k=3.
∴BC=12,AB=15.
∴AB+BC+AC=36.
cosA=
小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.994 5,
sin222°+sin268°≈0.372+0.932=1.001 8,
sin229°+sin261°≈0.482+0.872=0.987 3,
sin237°+sin253°≈0.602+0.802=1.000 0,
sin245°+sin245°=( )2+( )2=1.
据此,小明猜想:
对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(1)当α=30°时,验证sin2α+sin2(90°-α)=1是否成立.
(2)小明的猜想是否成立 若成立,请给予证明;若不成立,请举出一个反例.
(中考·乐山) 如图1,已知△ABC的三个顶点均在格点上,则cosA的值为( )
【解析】 D 如图,过点B 作BD⊥AC (点D正好在格点外),如图2,由勾股定理,得AB= ,AD= 所以cosA=
D
1.如图,在4×4的正方形方格中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正弦值是 .
2.在Rt△ABC中,∠C=90°,CD是斜边AB上的高,如果CD=3,BD=2,那么cos A的值是 .
D
A. 4 B. 6 C. 8 D. 10
2
3. 在Rt△ABC中,∠C=90°, ,BC=6,则 AB的长为 ( )
4. 在△ABC 中,∠C=90°,如果 ,AB=6,那么BC=_____.
锐角三角函数
定义:sinA,cosA
0
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
