【原创精品】人教版数学九年级下册 28.1.3 《特殊角的三角函数值》课件 (共20张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 28.1.3 《特殊角的三角函数值》课件 (共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览





文档简介
(共20张PPT)
28.1.3 特殊角的三角函数值
人教版九年级下册
第二十八章 锐角三角函数
1.理解30°、45°、60°角的三角函数值推导过程;
2.通过对特殊锐角三角函数值的探索,培养学生观察、比较、分析、概括的思维能力;
3. 培养学生良好的数形结合的能力,激发学生的求知欲和学习的自信心.
重点:熟记30°、45°、60°角的三角函数值.
难点:理解30°、45°、60°角的三角函数值推导过程.
学习目标
重点难点
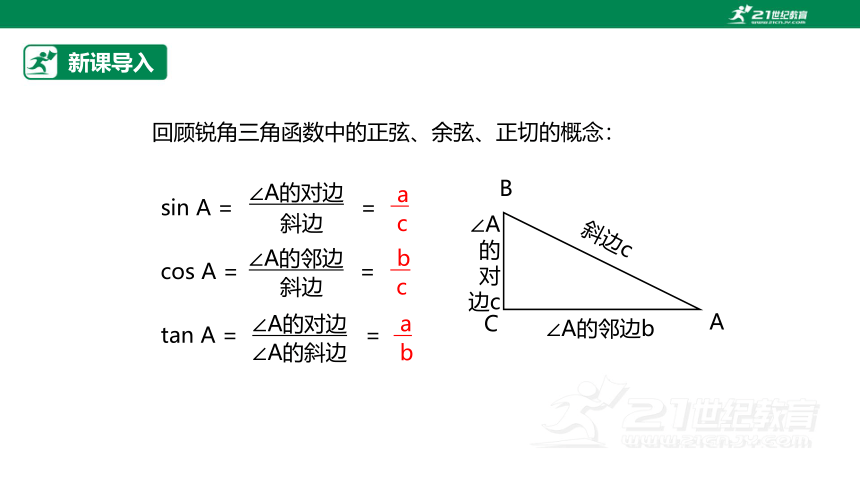
回顾锐角三角函数中的正弦、余弦、正切的概念:
A
C
斜边c
∠A的邻边b
∠A
的
对
边c
∠A的对边
斜边
sin A = =
c
a
∠A的邻边
斜边
cos A = =
c
b
∠A的对边
∠A的斜边
tan A = =
b
a
B
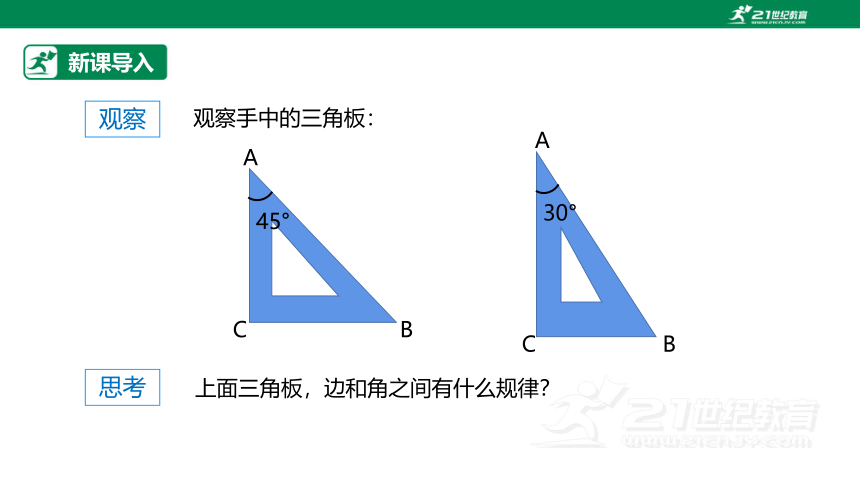
观察手中的三角板:
观察
A
B
C
45°
A
B
C
30°
上面三角板,边和角之间有什么规律?
思考
如图,在Rt△ABC中,∠C=90°,∠A=30°,则AB、BC、AC三边之间有什么关系?
A
C
B
解:根据直角三角形的性质可得:
根据勾股定理可得:
思考
能求出:sin 30°,cos 30°,tan 30°的三角函数值吗?
思考
能求出:sin 60°,cos 60°,tan 60°的三角函数值吗?
思考
能求出:sin 45°,cos 45°,tan 45°的三角函数值吗?
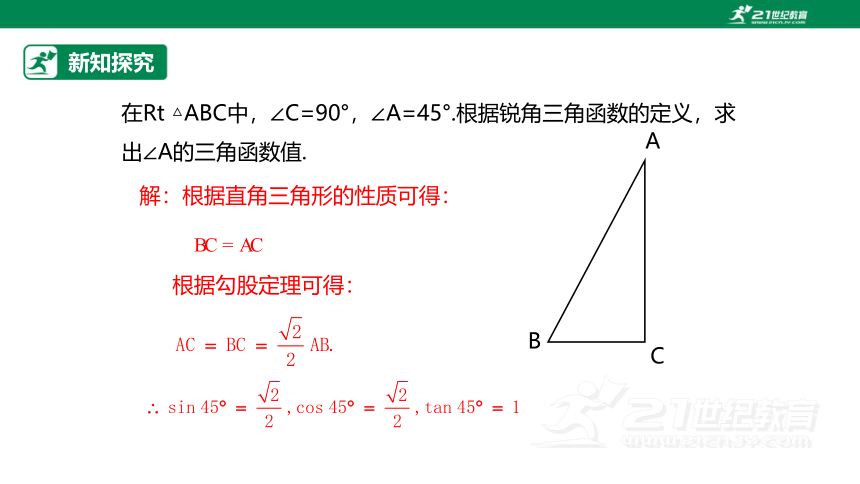
在Rt △ABC中,∠C=90°,∠A=45°.根据锐角三角函数的定义,求出∠A的三角函数值.
A
C
B
解:根据直角三角形的性质可得:
根据勾股定理可得:
30° 45° 60°
sin A
cos A
tan A
锐角A
锐角
三角函数
1
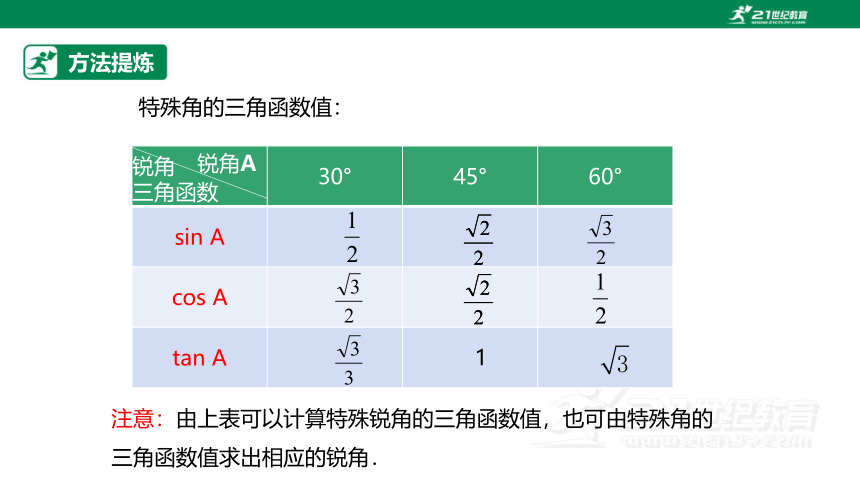
特殊角的三角函数值:
注意:由上表可以计算特殊锐角的三角函数值,也可由特殊角的三角函数值求出相应的锐角.
例1. 求值:sin 30° tan 30°+ cos60° tan60°.
解: sin 30° tan 30°+ cos60° tan60°
1. 三角板记忆法:借助如图所示的三角板记忆.
2.特点记忆法:30°,45°,60°角的正弦值记为
余弦值相反,正切值记为
3. 口诀记忆法:1,2,3;3,2,1;3,9,27;弦比2, 切比3,
分子根号别忘添.
300
1
2
450
1
1
特殊锐角三角函数值的方法:
A
1. 2cos60°=( )
A.1 B. C. D.
2. 计算:(2019-π)0 + -sin60°.
解:
原式=1+ -1 -
=
1. 2sin60°等于( )
A.1 B. C. D.
2.cos60°+ tan45°的值等于( )
A. B. C D.1
B
A
3. 已知α,β均为锐角,且满足
则 α+β=________.
75°
4.如图所示,小明家(图中的点O处)门前有一条东西走向的公路,有一水塔(图中的点A处)在她家北偏东60°方向的500 m处,过点A作AB⊥OB于点B,则点O到点B的距离是( )
B
5.一个小孩荡秋千,秋千链子的长度为4 m,秋千向两边摆动的幅度相同,简化图如图所示,OA,OB,OC均为秋千长,∠AOB为摆动角.当秋千升高2 m时,
求秋千的摆动角的度数.
O
A
B
C
D
∴秋千的摆动角∠AOB=∠AOD+∠BOD=120°.
解:由题意,得OA=OC=4 m,CD=2 m,
∴OD=2 m.
∵∠ADO=90°,
∴cos∠AOD= = ,
OA
2
OD
1
∴∠AOD=60°.
由题意可知∠BOD=∠AOD=60°,
特殊锐角的三角函数值
30°、45°和60°的三角函数值
由三角函数值求特殊角
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
28.1.3 特殊角的三角函数值
人教版九年级下册
第二十八章 锐角三角函数
1.理解30°、45°、60°角的三角函数值推导过程;
2.通过对特殊锐角三角函数值的探索,培养学生观察、比较、分析、概括的思维能力;
3. 培养学生良好的数形结合的能力,激发学生的求知欲和学习的自信心.
重点:熟记30°、45°、60°角的三角函数值.
难点:理解30°、45°、60°角的三角函数值推导过程.
学习目标
重点难点
回顾锐角三角函数中的正弦、余弦、正切的概念:
A
C
斜边c
∠A的邻边b
∠A
的
对
边c
∠A的对边
斜边
sin A = =
c
a
∠A的邻边
斜边
cos A = =
c
b
∠A的对边
∠A的斜边
tan A = =
b
a
B
观察手中的三角板:
观察
A
B
C
45°
A
B
C
30°
上面三角板,边和角之间有什么规律?
思考
如图,在Rt△ABC中,∠C=90°,∠A=30°,则AB、BC、AC三边之间有什么关系?
A
C
B
解:根据直角三角形的性质可得:
根据勾股定理可得:
思考
能求出:sin 30°,cos 30°,tan 30°的三角函数值吗?
思考
能求出:sin 60°,cos 60°,tan 60°的三角函数值吗?
思考
能求出:sin 45°,cos 45°,tan 45°的三角函数值吗?
在Rt △ABC中,∠C=90°,∠A=45°.根据锐角三角函数的定义,求出∠A的三角函数值.
A
C
B
解:根据直角三角形的性质可得:
根据勾股定理可得:
30° 45° 60°
sin A
cos A
tan A
锐角A
锐角
三角函数
1
特殊角的三角函数值:
注意:由上表可以计算特殊锐角的三角函数值,也可由特殊角的三角函数值求出相应的锐角.
例1. 求值:sin 30° tan 30°+ cos60° tan60°.
解: sin 30° tan 30°+ cos60° tan60°
1. 三角板记忆法:借助如图所示的三角板记忆.
2.特点记忆法:30°,45°,60°角的正弦值记为
余弦值相反,正切值记为
3. 口诀记忆法:1,2,3;3,2,1;3,9,27;弦比2, 切比3,
分子根号别忘添.
300
1
2
450
1
1
特殊锐角三角函数值的方法:
A
1. 2cos60°=( )
A.1 B. C. D.
2. 计算:(2019-π)0 + -sin60°.
解:
原式=1+ -1 -
=
1. 2sin60°等于( )
A.1 B. C. D.
2.cos60°+ tan45°的值等于( )
A. B. C D.1
B
A
3. 已知α,β均为锐角,且满足
则 α+β=________.
75°
4.如图所示,小明家(图中的点O处)门前有一条东西走向的公路,有一水塔(图中的点A处)在她家北偏东60°方向的500 m处,过点A作AB⊥OB于点B,则点O到点B的距离是( )
B
5.一个小孩荡秋千,秋千链子的长度为4 m,秋千向两边摆动的幅度相同,简化图如图所示,OA,OB,OC均为秋千长,∠AOB为摆动角.当秋千升高2 m时,
求秋千的摆动角的度数.
O
A
B
C
D
∴秋千的摆动角∠AOB=∠AOD+∠BOD=120°.
解:由题意,得OA=OC=4 m,CD=2 m,
∴OD=2 m.
∵∠ADO=90°,
∴cos∠AOD= = ,
OA
2
OD
1
∴∠AOD=60°.
由题意可知∠BOD=∠AOD=60°,
特殊锐角的三角函数值
30°、45°和60°的三角函数值
由三角函数值求特殊角
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
