【原创精品】人教版数学九年级下册 28.1.2 《正切函数》课件 (共20张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 28.1.2 《正切函数》课件 (共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览






文档简介
(共20张PPT)
28.1.2 正切函数
人教版九年级下册
第二十八章 锐角三角函数
1、理解正切的定义,能根据已知直角三角形的边长求一个锐角的正切值.
2、了解锐角A的三角函数的定义,能运用锐角三角函数的定义求三角函数值.
重点:正切的定义.
难点:已知直角三角形的边长求一个锐角的余弦值和正切值.
学习目标
重点难点
回顾相似三角形的性质:
相似三角形对应边上的高、中线、角平分线、周长的比等于相似比
相似三角形面积的比等于相似比的平方
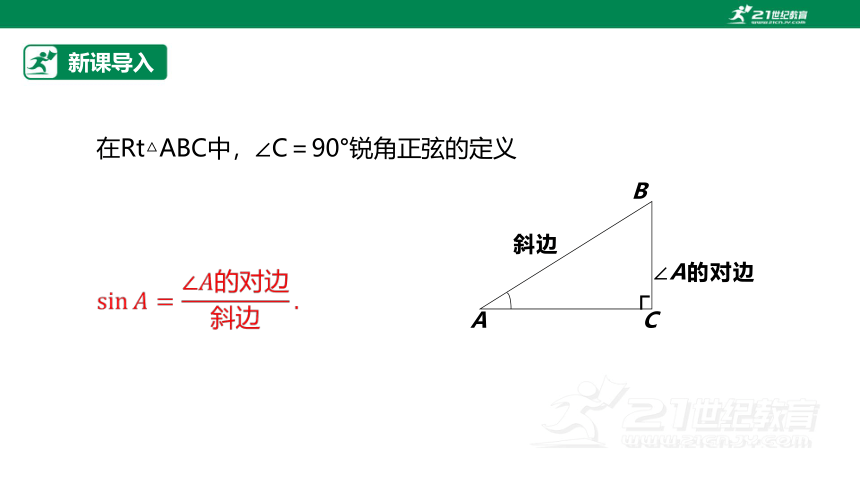
在Rt△ABC中,∠C=90°锐角正弦的定义
A
B
C
∠A的对边
┌
斜边
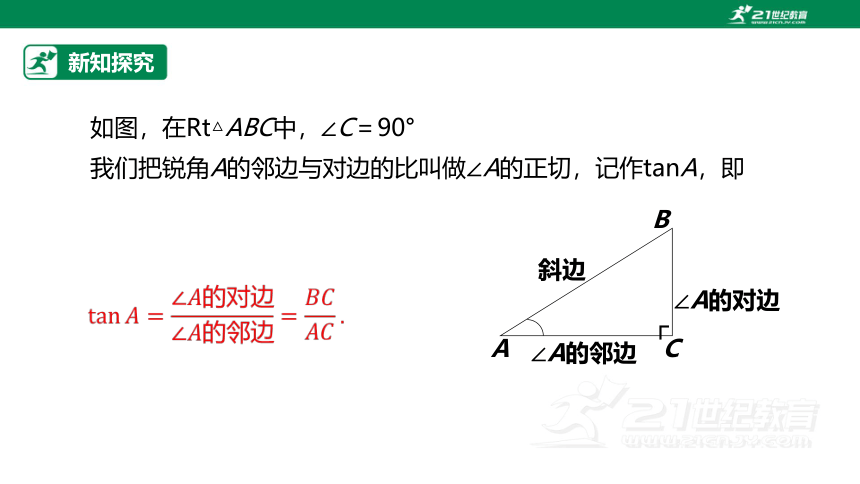
如图,在Rt△ABC中,∠C=90°
我们把锐角A的邻边与对边的比叫做∠A的正切,记作tanA,即
A
B
C
∠A的对边
┌
斜边
∠A的邻边
例1 如图,在 Rt△ABC 中,∠C =90°,AB=10,BC=6,求sin A, cos A,tan A的值.
A
B
C
已知直角三角形的任意两边长求某个锐角的三角函数值时,运用数形结合思想,首先画出符合题意的直角三角形,然后根据勾股定理求出未知边长,最后结合锐角三角函数的定义求三角函数值.
求三角函数值方法
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
A
B
C
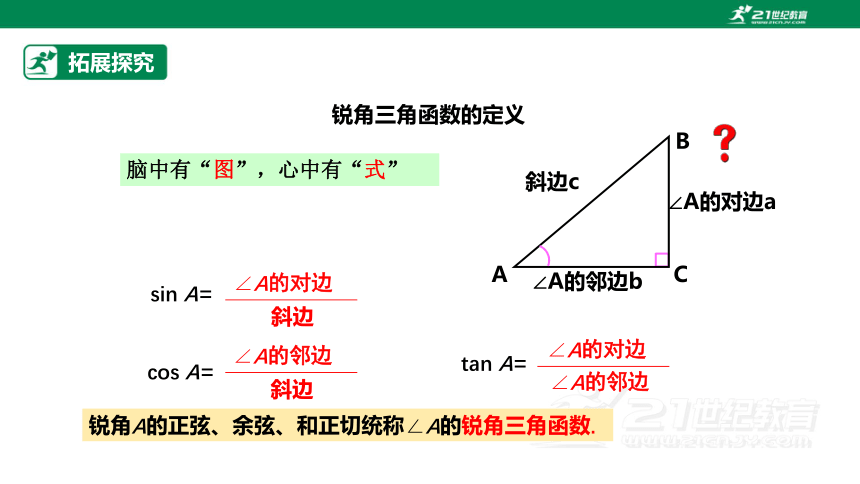
锐角A的正弦、余弦、和正切统称∠A的锐角三角函数.
sin A=
cos A=
tan A=
脑中有“图”,心中有“式”
锐角三角函数的定义
A
B
C
斜边c
∠A的邻边b
∠A的对边a
∠A的邻边
斜边
∠A的对边
斜边
∠A的对边
∠A的邻边
如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理,得
因此
已知直角三角形两边求锐角三角函数的值
已知直角三角形中的两条边求锐角三角函数值的一般思路是:当所涉及的边是已知时,直接利用定义求锐角三角函数值;当所涉及的边是未知时,可考虑运用勾股定理的知识求得边的长度,然后根据定义求锐角三角函数值.
利用勾股定理求三角函数值方法
1. 如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=______.
A
B
C
B
2. 如图,A , B , C 是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
A. B.1
C. D.
B
B
B
A
E
D
C
30°
A
B
A
B
C
α
B
∠A的对边与邻边的比叫做∠A 的正切,记作tan A,
即tan A=
A
B
C
∠A的对边a
┌
斜边c
∠A的邻边b
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
28.1.2 正切函数
人教版九年级下册
第二十八章 锐角三角函数
1、理解正切的定义,能根据已知直角三角形的边长求一个锐角的正切值.
2、了解锐角A的三角函数的定义,能运用锐角三角函数的定义求三角函数值.
重点:正切的定义.
难点:已知直角三角形的边长求一个锐角的余弦值和正切值.
学习目标
重点难点
回顾相似三角形的性质:
相似三角形对应边上的高、中线、角平分线、周长的比等于相似比
相似三角形面积的比等于相似比的平方
在Rt△ABC中,∠C=90°锐角正弦的定义
A
B
C
∠A的对边
┌
斜边
如图,在Rt△ABC中,∠C=90°
我们把锐角A的邻边与对边的比叫做∠A的正切,记作tanA,即
A
B
C
∠A的对边
┌
斜边
∠A的邻边
例1 如图,在 Rt△ABC 中,∠C =90°,AB=10,BC=6,求sin A, cos A,tan A的值.
A
B
C
已知直角三角形的任意两边长求某个锐角的三角函数值时,运用数形结合思想,首先画出符合题意的直角三角形,然后根据勾股定理求出未知边长,最后结合锐角三角函数的定义求三角函数值.
求三角函数值方法
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
A
B
C
锐角A的正弦、余弦、和正切统称∠A的锐角三角函数.
sin A=
cos A=
tan A=
脑中有“图”,心中有“式”
锐角三角函数的定义
A
B
C
斜边c
∠A的邻边b
∠A的对边a
∠A的邻边
斜边
∠A的对边
斜边
∠A的对边
∠A的邻边
如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理,得
因此
已知直角三角形两边求锐角三角函数的值
已知直角三角形中的两条边求锐角三角函数值的一般思路是:当所涉及的边是已知时,直接利用定义求锐角三角函数值;当所涉及的边是未知时,可考虑运用勾股定理的知识求得边的长度,然后根据定义求锐角三角函数值.
利用勾股定理求三角函数值方法
1. 如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=______.
A
B
C
B
2. 如图,A , B , C 是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
A. B.1
C. D.
B
B
B
A
E
D
C
30°
A
B
A
B
C
α
B
∠A的对边与邻边的比叫做∠A 的正切,记作tan A,
即tan A=
A
B
C
∠A的对边a
┌
斜边c
∠A的邻边b
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
