【原创精品】人教版数学九年级下册 28.2.1 《解直角三角形》课件 (共20张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 28.2.1 《解直角三角形》课件 (共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览








文档简介
(共20张PPT)
28.2.1 解直角三角形
人教版九年级下册
第二十八章 锐角三角函数
1.熟练地根据题目中的已知条件解直角三角形;
2.经历实际情境中锐角三角函数等有关概念的应用过程, 掌握解直角三角形的应用方法力;
3. 培养学生分析问题、解决问题 的能力,渗透数形结合的数学思想和方法.
重点:理解解直角三角形的概念.
难点:从条件出发,正确选用适当的边角关系解实际问题.
学习目标
重点难点
回顾直角三角形有关知识点:
A
C
斜边c
∠A的邻边b
∠A
的
对
边a
∠A的对边
斜边
sin A = =
c
a
∠A的邻边
斜边
cos A = =
c
b
∠A的对边
∠A的斜边
tan A = =
b
a
B
两锐角互余,即∠A+∠B=____;
角:
90°
边与边的关系:________________
边:
a2 + b2 = c2
边角:
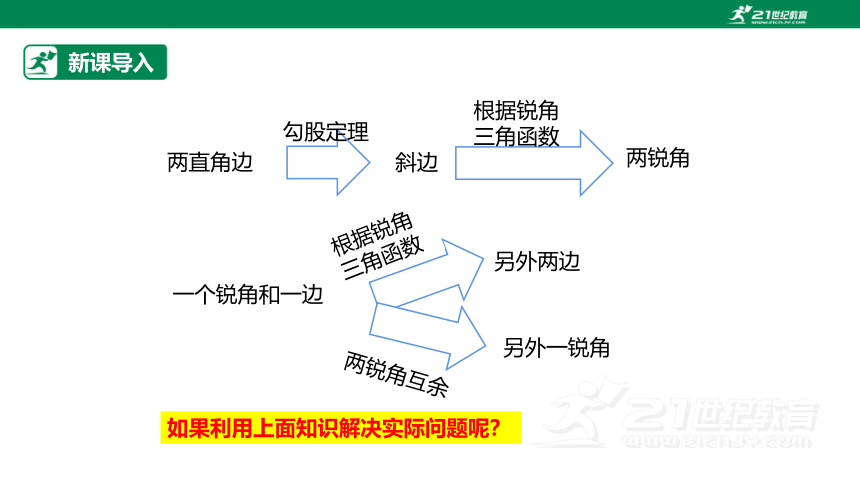
如果利用上面知识解决实际问题呢?
两锐角
两直角边
勾股定理
斜边
根据锐角
三角函数
一个锐角和一边
根据锐角
三角函数
另外两边
两锐角互余
另外一锐角
例1.如图,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根12米处,则大树在折断之前高多少?
解:利用勾股定理可以求出折断后倒下部分的长度为:
13+5=18(米)
答:大树在折断之前高18米
象这样,利用直角三角形的边角关系求出另外两个锐角,像这样,在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形
例2.如图,在相距2000米的东、西两座炮台A、B处同时发现入侵敌舰C,
在炮台A处测得敌舰C在它的南偏东40°的方向,在炮台B处测得敌舰C
在它的正南方,试求敌舰与两炮台的距离.(精确到1米)
解:在Rt△ABC中,
∵∠CAB=90°-∠DAC=50°,
∴BC=AB·tan∠CAB=2000×tam50°≈2384(米).
∠CAB,
(米)
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
(1)已知道两边
(2)已知一条边和一个锐角
解直角三角形类型题
如图,某水上乐园有一个滑梯AB,高度AC为6米,倾斜角为60°,暑期将至,为改善滑梯AB的安全性能,把倾斜角由60°减至30°.
A
C
B
D
300
600
6米
(1)求调整后的滑梯AD的长度;
(2)调整后的滑梯AD比原滑梯AB增加多少米 (精确到0.1米)
(参考数据: )
解:(1)Rt△ADC中,
因为∠ADB=30°,AC=6米,
所以AD=2AC=12米,
所以AD的长度为12米.
如图,某水上乐园有一个滑梯AB,高度AC为6米,倾斜角为60°,暑期将至,为改善滑梯AB的安全性能,把倾斜角由60°减至30°.
A
C
B
D
300
600
6米
(1)求调整后的滑梯AD的长度;
(2)调整后的滑梯AD比原滑梯AB增加多少米 (精确到0.1米)
(参考数据: )
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角形”,则tan A= .
或
好玩儿三角形!有意思吧!
解:如图作CH⊥AB于H.
在Rt△BCH中,∵BC=12,∠B=30°,
如图,在△ABC中,BC=12, ,B=30°;求AC和AB的长.
H
∴ , ,
∴ ,
∴AH=8,
在Rt△ACH中, ,
∴ .
C
A
1. 根据下列条件解直角三角形,结果不能确定的是( )
①已知一直角边及其对角;②已知两锐角;③已知两直角边;④已知一斜边和一锐角;⑤已知一直角边和斜边.
A.②③ B.②④ C.② D.②④⑤
C
4.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形:
(1)∠B=45°,c=14;
(2)b=15,∠B=60°.
解:(1)∵∠B=45°,c=14,∠C=90°,
∴∠A=45°,
4.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形:
(1)∠B=45°,c=14;
(2)b=15,∠B=60°.
解:(2)∵∠C=90°,∠B=60°,
∴∠A=30°.
∵b=15,
∴c= = = ,
sinB
sin60°
15
b
a= = = .
tanB
tan60°
15
b
5.如图,有一个三角形的钢架ABC,∠A=30°,∠C=45°,AC=2( + 1)m.
请计算说明,工人师傅搬运此钢架能否通过一个直径为2.1 m的圆形门
A
B
C
解:工人师傅搬运此钢架能通过一个直径为2.1 m的圆形门,
理由:
过B作BD⊥AC于D,如图:
设BD=x m,
∵∠A=30°,∠C=45°,
∴DC=BD=x m,AD= BD= x m,
概念
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
应用
已知两边解直角三角形
已知一边和一锐角解直角三角形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
28.2.1 解直角三角形
人教版九年级下册
第二十八章 锐角三角函数
1.熟练地根据题目中的已知条件解直角三角形;
2.经历实际情境中锐角三角函数等有关概念的应用过程, 掌握解直角三角形的应用方法力;
3. 培养学生分析问题、解决问题 的能力,渗透数形结合的数学思想和方法.
重点:理解解直角三角形的概念.
难点:从条件出发,正确选用适当的边角关系解实际问题.
学习目标
重点难点
回顾直角三角形有关知识点:
A
C
斜边c
∠A的邻边b
∠A
的
对
边a
∠A的对边
斜边
sin A = =
c
a
∠A的邻边
斜边
cos A = =
c
b
∠A的对边
∠A的斜边
tan A = =
b
a
B
两锐角互余,即∠A+∠B=____;
角:
90°
边与边的关系:________________
边:
a2 + b2 = c2
边角:
如果利用上面知识解决实际问题呢?
两锐角
两直角边
勾股定理
斜边
根据锐角
三角函数
一个锐角和一边
根据锐角
三角函数
另外两边
两锐角互余
另外一锐角
例1.如图,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根12米处,则大树在折断之前高多少?
解:利用勾股定理可以求出折断后倒下部分的长度为:
13+5=18(米)
答:大树在折断之前高18米
象这样,利用直角三角形的边角关系求出另外两个锐角,像这样,在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形
例2.如图,在相距2000米的东、西两座炮台A、B处同时发现入侵敌舰C,
在炮台A处测得敌舰C在它的南偏东40°的方向,在炮台B处测得敌舰C
在它的正南方,试求敌舰与两炮台的距离.(精确到1米)
解:在Rt△ABC中,
∵∠CAB=90°-∠DAC=50°,
∴BC=AB·tan∠CAB=2000×tam50°≈2384(米).
∠CAB,
(米)
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
(1)已知道两边
(2)已知一条边和一个锐角
解直角三角形类型题
如图,某水上乐园有一个滑梯AB,高度AC为6米,倾斜角为60°,暑期将至,为改善滑梯AB的安全性能,把倾斜角由60°减至30°.
A
C
B
D
300
600
6米
(1)求调整后的滑梯AD的长度;
(2)调整后的滑梯AD比原滑梯AB增加多少米 (精确到0.1米)
(参考数据: )
解:(1)Rt△ADC中,
因为∠ADB=30°,AC=6米,
所以AD=2AC=12米,
所以AD的长度为12米.
如图,某水上乐园有一个滑梯AB,高度AC为6米,倾斜角为60°,暑期将至,为改善滑梯AB的安全性能,把倾斜角由60°减至30°.
A
C
B
D
300
600
6米
(1)求调整后的滑梯AD的长度;
(2)调整后的滑梯AD比原滑梯AB增加多少米 (精确到0.1米)
(参考数据: )
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角形”,则tan A= .
或
好玩儿三角形!有意思吧!
解:如图作CH⊥AB于H.
在Rt△BCH中,∵BC=12,∠B=30°,
如图,在△ABC中,BC=12, ,B=30°;求AC和AB的长.
H
∴ , ,
∴ ,
∴AH=8,
在Rt△ACH中, ,
∴ .
C
A
1. 根据下列条件解直角三角形,结果不能确定的是( )
①已知一直角边及其对角;②已知两锐角;③已知两直角边;④已知一斜边和一锐角;⑤已知一直角边和斜边.
A.②③ B.②④ C.② D.②④⑤
C
4.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形:
(1)∠B=45°,c=14;
(2)b=15,∠B=60°.
解:(1)∵∠B=45°,c=14,∠C=90°,
∴∠A=45°,
4.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形:
(1)∠B=45°,c=14;
(2)b=15,∠B=60°.
解:(2)∵∠C=90°,∠B=60°,
∴∠A=30°.
∵b=15,
∴c= = = ,
sinB
sin60°
15
b
a= = = .
tanB
tan60°
15
b
5.如图,有一个三角形的钢架ABC,∠A=30°,∠C=45°,AC=2( + 1)m.
请计算说明,工人师傅搬运此钢架能否通过一个直径为2.1 m的圆形门
A
B
C
解:工人师傅搬运此钢架能通过一个直径为2.1 m的圆形门,
理由:
过B作BD⊥AC于D,如图:
设BD=x m,
∵∠A=30°,∠C=45°,
∴DC=BD=x m,AD= BD= x m,
概念
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
应用
已知两边解直角三角形
已知一边和一锐角解直角三角形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
