【原创精品】28.2.2.1 《解直角三角形的简单应用》 课件(共26张PPT)
文档属性
| 名称 | 【原创精品】28.2.2.1 《解直角三角形的简单应用》 课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览



文档简介
(共26张PPT)
28.2.2.1 解直角三角形的简单应用
人教版九年级下册
第二十八章 锐角三角函数
1.会把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决
2.渗透数学来源于实践又反过来作用于实践的观点,培养用数学的意识.
重点:利用所学知识解决实际问题..
难点:实际问题转化为数学模型.
学习目标
重点难点
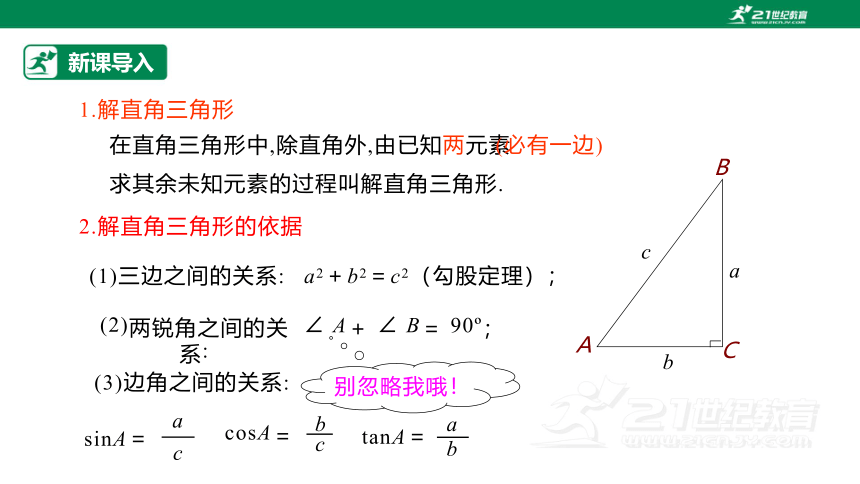
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
(必有一边)
A
C
B
a
b
c
别忽略我哦!
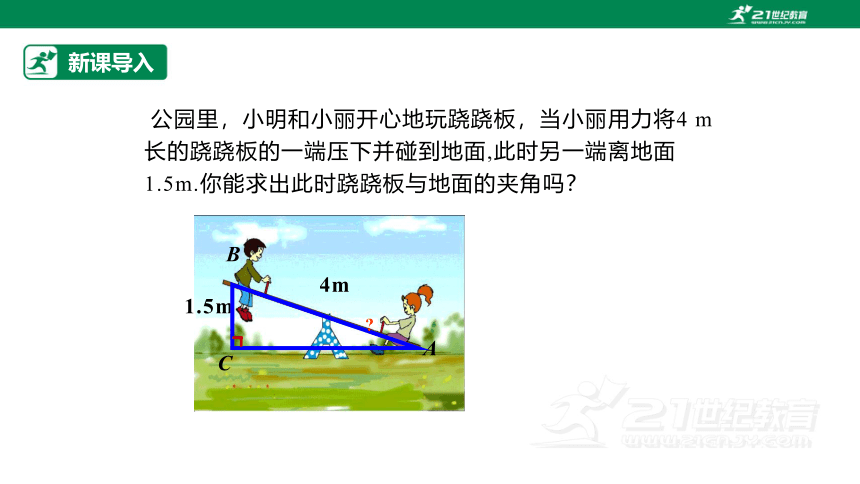
公园里,小明和小丽开心地玩跷跷板,当小丽用力将4 m长的跷跷板的一端压下并碰到地面,此时另一端离地面1.5m.你能求出此时跷跷板与地面的夹角吗?
4m
1.5m
A
B
C
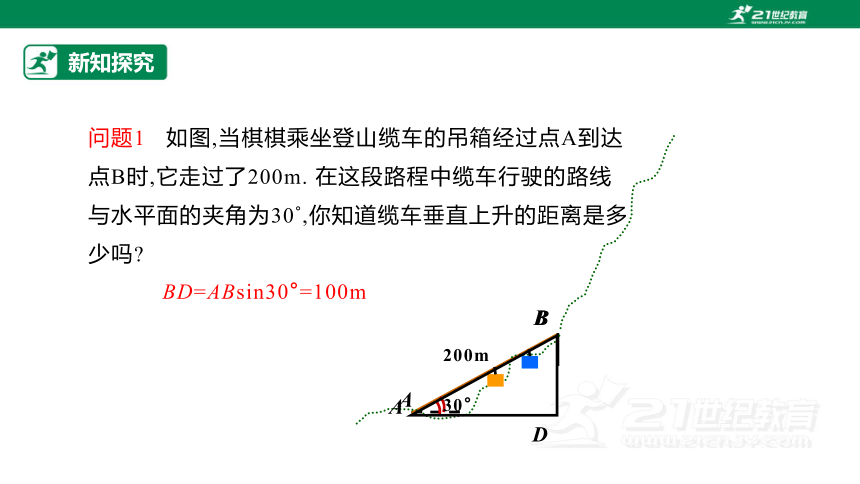
问题1 如图,当棋棋乘坐登山缆车的吊箱经过点A到达点B时,它走过了200m. 在这段路程中缆车行驶的路线与水平面的夹角为30°,你知道缆车垂直上升的距离是多少吗
A
B
A
B
D
30°
200m
BD=ABsin30°=100m
A
B
C
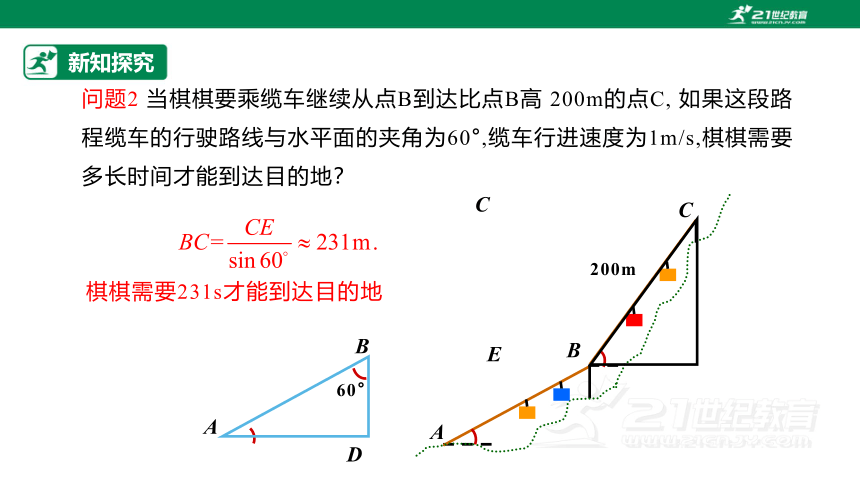
问题2 当棋棋要乘缆车继续从点B到达比点B高 200m的点C, 如果这段路程缆车的行驶路线与水平面的夹角为60°,缆车行进速度为1m/s,棋棋需要多长时间才能到达目的地?
A
B
D
C
E
60°
200m
棋棋需要231s才能到达目的地
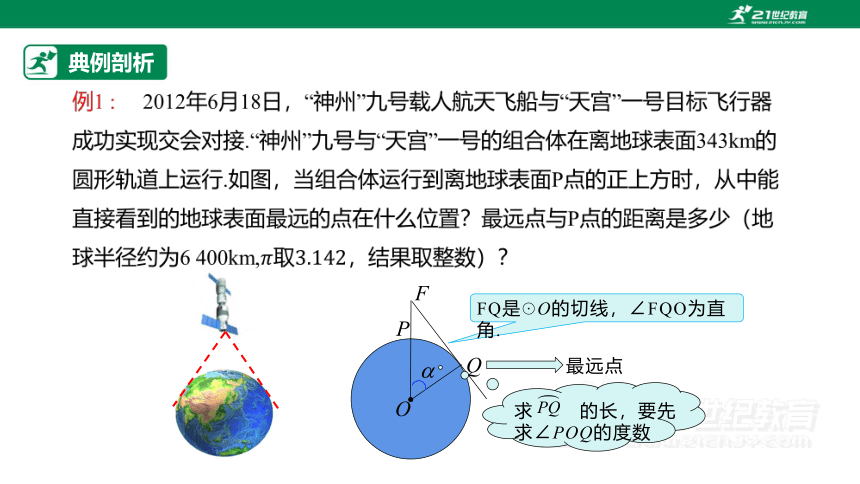
O
F
P
Q
FQ是☉O的切线,∠FQO为直角.
最远点
求 的长,要先求∠POQ的度数
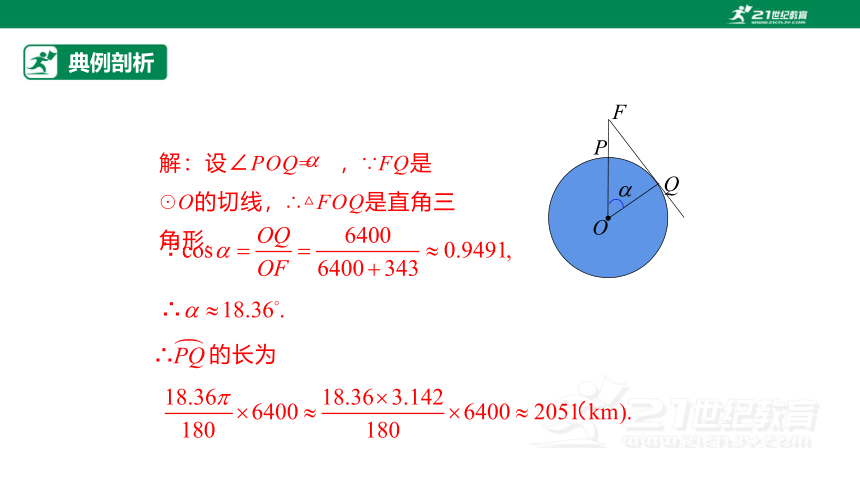
O
F
P
Q
解:设∠POQ= ,∵FQ是☉O的切线,∴△FOQ是直角三角形.
的长为
利用解直角三角形解决实际问题的一般过程:
1.将实际问题抽象为数学问题;
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
画出平面图形,转化为解直角三角形的问题
3.得到数学问题的答案;
4.得到实际问题的答案.
例2 如图,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离为多少?
0.5m
3m
60°
0.5m
3m
A
B
C
D
E
60°
分析:根据题意,可知秋千踏板与地面的最大距离为CE的长度.
已知 :DE=0.5m,
AD=AB=3m,∠DAB=60°,△ACB为直角三角形.
建立数学模型
解:∵∠CAB=60°,AD=AB=3m,
3m
A
B
D
E
60°
C
∴AC=ABcos∠CAB=1.5m,
∴ CD=AD-AC=1.5m,
∴ CE=AD+DE=2.0m.
即秋千踏板与地面的最大距离为2.0m.
F
E
A
30°
15m
小华去实验楼做实验, 两幢实验楼的高度AB=CD=20m, 两楼间的距离BC=15m,已知太阳光与水平线的夹角为30°,求南楼的影子在北楼上有多高?
北
A
B
D
C
20m
15m
E
F
南
解:过点E作EF∥BC,
∴∠AFE=90°,FE=BC=15m.
即南楼的影子在北楼上的高度为
小华想:若设计时要求北楼的采光,不受南楼的影响,请问楼间距BC长至少应为多少米
A
B
20m
m
北
D
C
南
BC至少为
1.星期天,小华去图书超市购书,因他所买书类在二楼,故他乘电梯上楼,已知电梯AB段的长度8 m,倾斜角为300,则二楼的高度(相对于底楼)是__________m.
A
B
C
300
4
2.如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于_____________米.
mtanα
图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).
图1
图2
解:作CE⊥BD于E,AF⊥CE于F,易得四边形AHEF为矩形,
∴EF=AH=3.4m,∠HAF=90°.
∴∠CAF=∠CAH﹣∠HAF=118°﹣90°=28°.
在Rt△ACF中,∵ ,
∴CF=9sin28°=9×0.47=4.23,
∴CE=CF+EF=4.23+3.4≈7.6(m),
答:操作平台C离地面的高度为7.6m.
图2
E
F
1、我校准备在田径场旁建①②两幢学生公寓,已知每幢公寓的高为15米,太阳光线AC的入射角∠ACD=550,为使②公寓的从第一层起照到阳光,现请你设计一下,两幢公寓间距BC至少是( ) 米.
A.15sin55° B.15cos55° C.15tan55° D.15cot55°
C
2.一次台风将一棵大树刮断,经测量,大树刮断一端的着地点A到树根部C的距离为4米,倒下部分AB与地平面AC的夹角为45°,则这棵大树高是__________米.
A
C
B
3.如图,为固定电线杆AC,在离地面高度为6m的A处引拉线AB,使拉线AB与地面上的BC的夹角为48°,则拉线AB的长度约为 ( )
(结果精确到0.1m,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)
A.6.7m B.7.2m C.8.1m D.9.0m
C
4.数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两树距离的有( )
A.0组 B.1组
C.2组 .3组
D
5.某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为30°时,问:超市以上的居民住房采光是否有影响,为什么?
30°
太阳光
A
B
D
C
新楼
住宅楼
E
F
30°
利用解直角三角形解决实际问题的一般过程:
1.将实际问题抽象为数学问题;
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
画出平面图形,转化为解直角三角形的问题
3.得到数学问题的答案;
4.得到实际问题的答案.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
28.2.2.1 解直角三角形的简单应用
人教版九年级下册
第二十八章 锐角三角函数
1.会把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决
2.渗透数学来源于实践又反过来作用于实践的观点,培养用数学的意识.
重点:利用所学知识解决实际问题..
难点:实际问题转化为数学模型.
学习目标
重点难点
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
(必有一边)
A
C
B
a
b
c
别忽略我哦!
公园里,小明和小丽开心地玩跷跷板,当小丽用力将4 m长的跷跷板的一端压下并碰到地面,此时另一端离地面1.5m.你能求出此时跷跷板与地面的夹角吗?
4m
1.5m
A
B
C
问题1 如图,当棋棋乘坐登山缆车的吊箱经过点A到达点B时,它走过了200m. 在这段路程中缆车行驶的路线与水平面的夹角为30°,你知道缆车垂直上升的距离是多少吗
A
B
A
B
D
30°
200m
BD=ABsin30°=100m
A
B
C
问题2 当棋棋要乘缆车继续从点B到达比点B高 200m的点C, 如果这段路程缆车的行驶路线与水平面的夹角为60°,缆车行进速度为1m/s,棋棋需要多长时间才能到达目的地?
A
B
D
C
E
60°
200m
棋棋需要231s才能到达目的地
O
F
P
Q
FQ是☉O的切线,∠FQO为直角.
最远点
求 的长,要先求∠POQ的度数
O
F
P
Q
解:设∠POQ= ,∵FQ是☉O的切线,∴△FOQ是直角三角形.
的长为
利用解直角三角形解决实际问题的一般过程:
1.将实际问题抽象为数学问题;
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
画出平面图形,转化为解直角三角形的问题
3.得到数学问题的答案;
4.得到实际问题的答案.
例2 如图,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离为多少?
0.5m
3m
60°
0.5m
3m
A
B
C
D
E
60°
分析:根据题意,可知秋千踏板与地面的最大距离为CE的长度.
已知 :DE=0.5m,
AD=AB=3m,∠DAB=60°,△ACB为直角三角形.
建立数学模型
解:∵∠CAB=60°,AD=AB=3m,
3m
A
B
D
E
60°
C
∴AC=ABcos∠CAB=1.5m,
∴ CD=AD-AC=1.5m,
∴ CE=AD+DE=2.0m.
即秋千踏板与地面的最大距离为2.0m.
F
E
A
30°
15m
小华去实验楼做实验, 两幢实验楼的高度AB=CD=20m, 两楼间的距离BC=15m,已知太阳光与水平线的夹角为30°,求南楼的影子在北楼上有多高?
北
A
B
D
C
20m
15m
E
F
南
解:过点E作EF∥BC,
∴∠AFE=90°,FE=BC=15m.
即南楼的影子在北楼上的高度为
小华想:若设计时要求北楼的采光,不受南楼的影响,请问楼间距BC长至少应为多少米
A
B
20m
m
北
D
C
南
BC至少为
1.星期天,小华去图书超市购书,因他所买书类在二楼,故他乘电梯上楼,已知电梯AB段的长度8 m,倾斜角为300,则二楼的高度(相对于底楼)是__________m.
A
B
C
300
4
2.如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于_____________米.
mtanα
图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).
图1
图2
解:作CE⊥BD于E,AF⊥CE于F,易得四边形AHEF为矩形,
∴EF=AH=3.4m,∠HAF=90°.
∴∠CAF=∠CAH﹣∠HAF=118°﹣90°=28°.
在Rt△ACF中,∵ ,
∴CF=9sin28°=9×0.47=4.23,
∴CE=CF+EF=4.23+3.4≈7.6(m),
答:操作平台C离地面的高度为7.6m.
图2
E
F
1、我校准备在田径场旁建①②两幢学生公寓,已知每幢公寓的高为15米,太阳光线AC的入射角∠ACD=550,为使②公寓的从第一层起照到阳光,现请你设计一下,两幢公寓间距BC至少是( ) 米.
A.15sin55° B.15cos55° C.15tan55° D.15cot55°
C
2.一次台风将一棵大树刮断,经测量,大树刮断一端的着地点A到树根部C的距离为4米,倒下部分AB与地平面AC的夹角为45°,则这棵大树高是__________米.
A
C
B
3.如图,为固定电线杆AC,在离地面高度为6m的A处引拉线AB,使拉线AB与地面上的BC的夹角为48°,则拉线AB的长度约为 ( )
(结果精确到0.1m,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)
A.6.7m B.7.2m C.8.1m D.9.0m
C
4.数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两树距离的有( )
A.0组 B.1组
C.2组 .3组
D
5.某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为30°时,问:超市以上的居民住房采光是否有影响,为什么?
30°
太阳光
A
B
D
C
新楼
住宅楼
E
F
30°
利用解直角三角形解决实际问题的一般过程:
1.将实际问题抽象为数学问题;
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
画出平面图形,转化为解直角三角形的问题
3.得到数学问题的答案;
4.得到实际问题的答案.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
