【原创精品】28.2.2.2 《利用仰俯角解直角三角形》 课件(共19张PPT)
文档属性
| 名称 | 【原创精品】28.2.2.2 《利用仰俯角解直角三角形》 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览






文档简介
(共19张PPT)
28.2.2.2 利用仰俯角解直角三角形
人教版九年级下册
第二十八章 锐角三角函数
1.熟练地运用这些概念来解决一些实际问题;
2.培养学生将实际问题抽象成数学模型并进行解释与应用的能力;
3. 培养学生分析问题、解决问题 的能力,渗透数形结合的数学思想和方法.
重点:理解仰角和俯角的概念.
难点:能运用仰角和俯角的概念解决有关的实际问题.
学习目标
重点难点
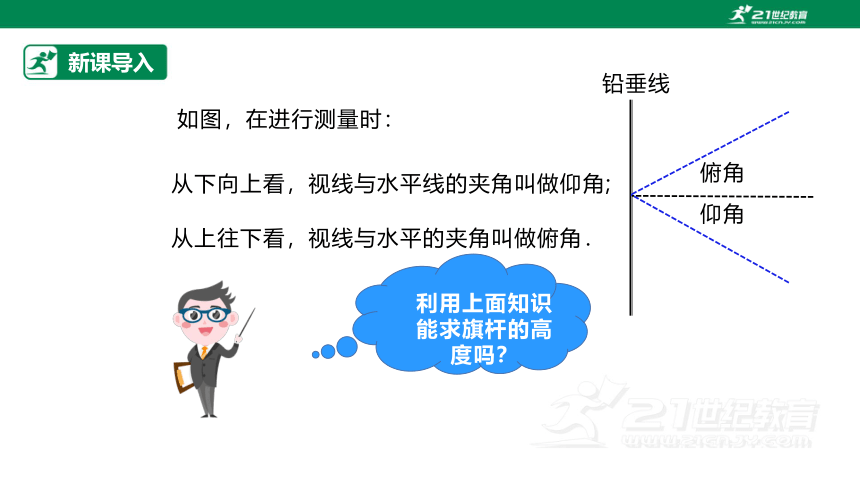
如图,在进行测量时:
从上往下看,视线与水平的夹角叫做俯角.
从下向上看,视线与水平线的夹角叫做仰角;
铅垂线
仰角
俯角
利用上面知识能求旗杆的高度吗?
例1:如图:为了测量旗杆的高度BC,在离旗杆底部10米的A处,用高1.50米的测角仪DA测得旗杆顶端C的仰角α=52°,求旗杆BC的高.(精确到0.1米)
解:在Rt△CDE中
∵CE=DE×tanα
=AB×tanα
=10×tan52°
≈12.80,
∴BC=BE+CE=DA+CE≈1.50+12.80=14.3(米)
答:旗杆BC的高度约为14.3米
仰角和俯角问题
解直角三角形
你能仿着例1的方法,求出课本第100页中旗杆的高度吗?
如下图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC=34°,并已知目高AD为1.50米
求旗杆BE的高.(精确到0.1米)
解:在Rt△ABC中
∵BC=AC×tanα
=10×tan34°
≈6.75,
∴BE=BC+CE≈1.50+6.75=8.3(米)
答:旗杆BE的高度约为8.3米
在解决仰角,俯角问题时,通常要添加辅助线,构造直角三角形,然后解直角三角形.
仰角、俯角问题
解:由C点向AB作垂线,交AB的延长线于E点,
并交海面于F点.
F
已知AB=4 000(米),∠BAC=30°,∠EBC=60°.
∵∠BCA=∠EBC-∠BAC=30°,
∴∠BAC=∠BCA.
∴BC=BA=4 000(米).
“数学活动小组”成员小亮为了测得如图所放风筝的高度,
进行了如下操作:
α
如图,某地修建高速公路,要从A地向B 地修一条隧道(点A、B 在同一水平面上).为了测量A、B 两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C 处,在C 处观察B地的俯角为α,则A、B两地之间的距离为( )
A. 800sinα米 B. 800tanα米
C. 米 D. 米
D
1. 如图①,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=_100_米.
A
300
4.“平阳府有座大鼓楼,半截子插在天里头.”说的是坐落在临汾市区的大中楼,
俗称鼓楼,龙盘虎踞,冲大而立,以其高大雄伟著称于世.如图,为测量鼓楼的高AB,
在距B点50 m的C处安装测倾器,测得鼓楼顶端A的仰角为40°12′,
测倾器的高CD为1.3 m,则鼓楼高AB约为 m(tan 40°12′≈0.85).
43.8
解:在Rt△BCD中,BD=9米,∠BCD=45°,
∴BD=CD=9米.
在Rt△ACD中,CD=9米,∠ACD=37°,
∴AD=CD·tan37°≈9×0.75=6.75(米),
AB=AD+BD=15.75(米),
整个过程中旗子上升高度是15.75-2.25=13.5(米),
仰角与俯角
概念
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平的夹角叫做俯角.
应用
添加辅助线,构造直角三角形,然后解直角三角形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
28.2.2.2 利用仰俯角解直角三角形
人教版九年级下册
第二十八章 锐角三角函数
1.熟练地运用这些概念来解决一些实际问题;
2.培养学生将实际问题抽象成数学模型并进行解释与应用的能力;
3. 培养学生分析问题、解决问题 的能力,渗透数形结合的数学思想和方法.
重点:理解仰角和俯角的概念.
难点:能运用仰角和俯角的概念解决有关的实际问题.
学习目标
重点难点
如图,在进行测量时:
从上往下看,视线与水平的夹角叫做俯角.
从下向上看,视线与水平线的夹角叫做仰角;
铅垂线
仰角
俯角
利用上面知识能求旗杆的高度吗?
例1:如图:为了测量旗杆的高度BC,在离旗杆底部10米的A处,用高1.50米的测角仪DA测得旗杆顶端C的仰角α=52°,求旗杆BC的高.(精确到0.1米)
解:在Rt△CDE中
∵CE=DE×tanα
=AB×tanα
=10×tan52°
≈12.80,
∴BC=BE+CE=DA+CE≈1.50+12.80=14.3(米)
答:旗杆BC的高度约为14.3米
仰角和俯角问题
解直角三角形
你能仿着例1的方法,求出课本第100页中旗杆的高度吗?
如下图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC=34°,并已知目高AD为1.50米
求旗杆BE的高.(精确到0.1米)
解:在Rt△ABC中
∵BC=AC×tanα
=10×tan34°
≈6.75,
∴BE=BC+CE≈1.50+6.75=8.3(米)
答:旗杆BE的高度约为8.3米
在解决仰角,俯角问题时,通常要添加辅助线,构造直角三角形,然后解直角三角形.
仰角、俯角问题
解:由C点向AB作垂线,交AB的延长线于E点,
并交海面于F点.
F
已知AB=4 000(米),∠BAC=30°,∠EBC=60°.
∵∠BCA=∠EBC-∠BAC=30°,
∴∠BAC=∠BCA.
∴BC=BA=4 000(米).
“数学活动小组”成员小亮为了测得如图所放风筝的高度,
进行了如下操作:
α
如图,某地修建高速公路,要从A地向B 地修一条隧道(点A、B 在同一水平面上).为了测量A、B 两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C 处,在C 处观察B地的俯角为α,则A、B两地之间的距离为( )
A. 800sinα米 B. 800tanα米
C. 米 D. 米
D
1. 如图①,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=_100_米.
A
300
4.“平阳府有座大鼓楼,半截子插在天里头.”说的是坐落在临汾市区的大中楼,
俗称鼓楼,龙盘虎踞,冲大而立,以其高大雄伟著称于世.如图,为测量鼓楼的高AB,
在距B点50 m的C处安装测倾器,测得鼓楼顶端A的仰角为40°12′,
测倾器的高CD为1.3 m,则鼓楼高AB约为 m(tan 40°12′≈0.85).
43.8
解:在Rt△BCD中,BD=9米,∠BCD=45°,
∴BD=CD=9米.
在Rt△ACD中,CD=9米,∠ACD=37°,
∴AD=CD·tan37°≈9×0.75=6.75(米),
AB=AD+BD=15.75(米),
整个过程中旗子上升高度是15.75-2.25=13.5(米),
仰角与俯角
概念
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平的夹角叫做俯角.
应用
添加辅助线,构造直角三角形,然后解直角三角形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
