【原创精品】人教版数学九年级下册 29.1.2 《平行投影》课件 (共29张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 29.1.2 《平行投影》课件 (共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览








文档简介
(共29张PPT)
29.1.2 平行投影
人教版九年级下册
第二十九章 投影与视图
1. 理解解平行投影与正投影的含义.
2. 理解平行投影与中心投影的区别与联系.
3. 理解平行投影的特点.
4. 会画平行投影投影的影子和解决实际问题.
重点:平行投影的含义.
难点:利用平行投影解决实际问题.
学习目标
重点难点
物体在太阳光下形成的影了与在灯光下形成的影了有什么不同呢
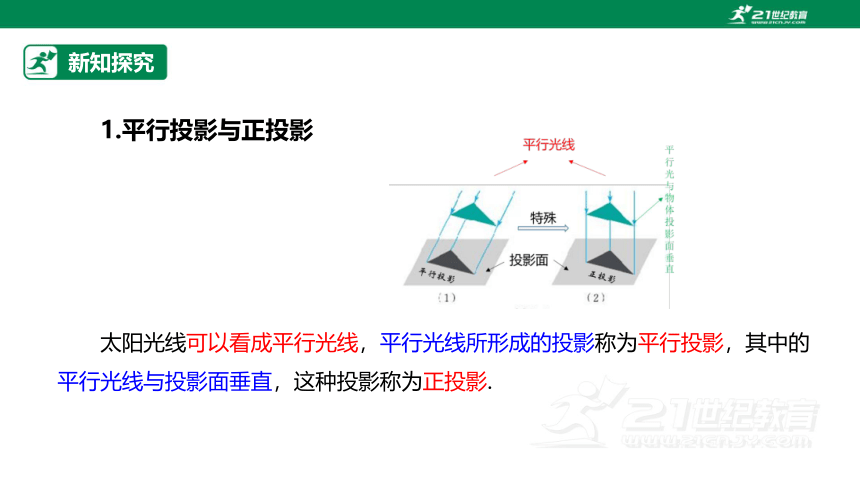
1.平行投影与正投影
太阳光线可以看成平行光线,平行光线所形成的投影称为平行投影,其中的平行光线与投影面垂直,这种投影称为正投影.
拓展
(1)在太阳光下,物体的影子随着时间的变化而变化,从早晨到傍晚,物体影子的指向是:正西→西北+正北→东北正东(北半球).一天之中,同一物体其影子的长短的变化规律是:长→短→最短→短→长.
(2)在正投影下,投影的变化规律为:物体平行于投影面时,投影现原形;物体倾斜于投影面时,投影改变;物体垂直于投影面时,面变线、线变点、点的正投影仍是点.
(1)等高的物体垂直于地面放置时,在太阳光下它们的影子一样长;
(2)等长的物体平行于地面放置时,在太阳光下它们的影子一样长,且影长等于物体本身的长度;
(3)同一时刻,在太阳光下,不同物体的高度比与其形长比相等.
2.平行投影与中心投影的联系与区别
联系:
(1)都是物体在光线下形成的影子.
(2)在平行投影中,同一时刻改变物体的位置和方向,其投影也跟着发生变化;
在中心投影中同一灯光下改变物体的位置和方向.其投影也跟看发生变化.
2.平行投影与中心投影的联系与区别
区别:
平行投影:(1)光源是太阳,光线是平行的;(2)同一时制,不同物体的影长与物高成比例;(3)同一时刻,物体影子的方向总相同.
中心投影:(1)光源是灯光等点光源,光线是发散的;
(2)即使在同时刻,影长与物高也不一定成比例;
(3)中心投影下,物体影子可能在同一方向,也可能在不同的方向即物体影子随点光源的位置的变化面变化.
(1)看光源,由点光源形成的投制是中心投影:由大阳光形成的授影属于平行投影.
(2)看光线,如果光线是平行的,所得到的投影就是平行投影,如果光线相交于一点,所得到的投影就是中心投影.
识别投影的方法
1.太阳光下的影子变化规律
例1 如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( )
A.①②③④ B.④①③② C.④②③① D.④③②①
B
一天中不同时刻物体影子的长短和方向是不同的,在北半球(以冬季为例),一天中不同的时刻,影子的方向是按“正西→西北→正北→东北→正东”的顺序变化的;影子的长短是从早晨到中午由长逐渐变短,从中午到下午由短逐渐变长的.
影子的长短和方向的变化规律
如图a,b,c,d是一物体在不同时刻阳光下的影子情况,按照时间的先后顺序正确的是( )
A.a-b-c-d B.a-c-b-d C.d-c-b-a D.d-b-c-a.
B
2. 太阳光影子的应用
例2 如图所示,已知AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影。
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长。
解(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影。
(2)∵AC∥DF,∴∠ACB=∠DFE,
∵∠ABC=∠DEF=90°,
∴ ABC∽ DEF,
∴AB/DE=BC/EF,∴5/DE=3/6,
∴DE=10m.
F
同一时刻的平行投影中,(1)物体与影子上的对应点的连线互相平行;(2)物高与影长的比相等.
平等投影的规律
如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在相同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为6米,留在墙上的影高为2米,求旗杆的高度.
解:过C作CE⊥AB于E,连接AC.
∵CD⊥BD,AB⊥BD,
∴∠EBD=∠CDB=∠CEB=90°,∴四边形CDBE为矩形,
∴BD=CE=6,CD=BE=2.
设AE=x米,则1:1.5=x:6,
解得:x=4.
故旗杆高AB=AE+BE=4+2=6(米).
3.正投影
例3 一个圆柱如图,已知该圆柱的正投影是边长为4 cm的正方形,求圆柱的体积和表面积.
解:因为圆柱的正投影是边长为4cm的正方形,
所以圆柱的底面半径为2cm,高为4cm.
因此圆柱的两个底面的面积之和为:2×π×2 =8π(平方厘米)
圆柱的侧面面积为:4π×4=16π(平方厘米)
所以圆柱的表面积为S=24π(平方厘米).
圆柱的体积为:V=π×2 ×4=16π(立方厘米)
(1)物体的正投影可看作是从观察方向看到的物体的最大截面图形;
(2)正投影计算的关键是找准物体与其正投影之间的对应关系,然后根据图形的相关计算公式进行计算.
方法总结
如图,从左面看圆柱,则图中圆柱的投影是( )
A.圆 B.矩形 C.梯形 D.圆柱
B
兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,求树的高度.
解:如图,
设树的高度为AB,BD为落在地面的影长,CE为落在台阶上的影长,CD为台阶高
延长EC交AB于F,则四边形BDCF是矩形,
从而FC=BD=4.4,BF=CD=0.3,
所以EF=4.4+0.2=4.6,
则 AF/1= 4.6/0.4
解得AF=11.5,AB=AF+FB=11.5+0.3=11.8(米).
所以树的高度AB为11.8米.
故答案为:11.8米。
(中考. 伊春)在阳光的照射下,一块三角板的投影不会是( D )
A.线段 B,与原三角形全等的三角形 C.变形的三角形 D.点
【分析】 将一个三角板放在太阳光下,当它与阳光平行时,它所形成的投影是一条线段:当它与阳光成一定角度但不垂直时,它所形威的投影是三角形.
【解答】 解:根据太阳高度角不同,所形成的投影也不同,当三角板与阳光平行时,所形成的投影为一条线,当它与阳光形成一定角度但不垂直时,它所形成的投影是三角形,不可能是一个点,故选: D,
1.在同一时刻的阳光下,小明的影子比小强的影子长,那么在另一时刻(位置不变),则( )
A.小明的影子比小强的影子长
B.小明的影子比小强的影子短
C.两个人的影子一样长
D.无法判断谁的影子长
解析:因为阳光的光线是平行的,由条件可知小明的身高比小强的身高高,所以在另一时刻小明的影子也比小强的影子长.
A
2.在同一时刻,两根长度不等的竿子置于阳光之下,但它们的影子相等,那么这两根竿子的相对位置是( )
A.都垂直于地面 B.平行斜插在地上
C.不平行斜插在地上 D.都倒在地上
C
3.在阳光下同一时刻,身高1.4 m的小强影长1 m,旗杆影长15 m,则旗杆的高为____m.
4.如图,小明在A时刻测得某树的影长为2 m,在B时刻又测得该树的影长为8 m,若两次日照的光线互相垂直,则树的高度为____m.
21
4
5.某数学课外实验小组想利用树影测量树高.阳光下,他们在同一时刻测得一身高为1.5 m的同学影长为1.35 m,因为大树靠近一幢建筑物,影子不全在地面上(如图),他们测得地面部分的影长BC=3.6 m,墙上影长CD=1.8 m,则树高AB为____m.
5.8
6.已知:如图,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻,AB在阳光下的投影BC=4 m.
(1)请你在图中画出此时DE在阳光下的投影,并简述画图步骤;
(2)在测量AB的投影长时,同时测出DE在阳光下的投影长为6 m,请你计算DE的长.
解:(1)如图:
作法:连接AC,过点D作DF∥AC,交直线BE于点F,则EF就是DE的投影.
(2)由(1)知DF∥AC,∴∠ACB=∠DFE.
又∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF.
∴AB/DE=BC/EF,∴5/DE=4/6,
∴DE=7.5(m).
平行投影
平行投影与中心投影的关系
正投影
平行投影的特点
平行投影的作图
利用平行投影与正投影的特点解决实际问题
平行投影
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
29.1.2 平行投影
人教版九年级下册
第二十九章 投影与视图
1. 理解解平行投影与正投影的含义.
2. 理解平行投影与中心投影的区别与联系.
3. 理解平行投影的特点.
4. 会画平行投影投影的影子和解决实际问题.
重点:平行投影的含义.
难点:利用平行投影解决实际问题.
学习目标
重点难点
物体在太阳光下形成的影了与在灯光下形成的影了有什么不同呢
1.平行投影与正投影
太阳光线可以看成平行光线,平行光线所形成的投影称为平行投影,其中的平行光线与投影面垂直,这种投影称为正投影.
拓展
(1)在太阳光下,物体的影子随着时间的变化而变化,从早晨到傍晚,物体影子的指向是:正西→西北+正北→东北正东(北半球).一天之中,同一物体其影子的长短的变化规律是:长→短→最短→短→长.
(2)在正投影下,投影的变化规律为:物体平行于投影面时,投影现原形;物体倾斜于投影面时,投影改变;物体垂直于投影面时,面变线、线变点、点的正投影仍是点.
(1)等高的物体垂直于地面放置时,在太阳光下它们的影子一样长;
(2)等长的物体平行于地面放置时,在太阳光下它们的影子一样长,且影长等于物体本身的长度;
(3)同一时刻,在太阳光下,不同物体的高度比与其形长比相等.
2.平行投影与中心投影的联系与区别
联系:
(1)都是物体在光线下形成的影子.
(2)在平行投影中,同一时刻改变物体的位置和方向,其投影也跟着发生变化;
在中心投影中同一灯光下改变物体的位置和方向.其投影也跟看发生变化.
2.平行投影与中心投影的联系与区别
区别:
平行投影:(1)光源是太阳,光线是平行的;(2)同一时制,不同物体的影长与物高成比例;(3)同一时刻,物体影子的方向总相同.
中心投影:(1)光源是灯光等点光源,光线是发散的;
(2)即使在同时刻,影长与物高也不一定成比例;
(3)中心投影下,物体影子可能在同一方向,也可能在不同的方向即物体影子随点光源的位置的变化面变化.
(1)看光源,由点光源形成的投制是中心投影:由大阳光形成的授影属于平行投影.
(2)看光线,如果光线是平行的,所得到的投影就是平行投影,如果光线相交于一点,所得到的投影就是中心投影.
识别投影的方法
1.太阳光下的影子变化规律
例1 如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( )
A.①②③④ B.④①③② C.④②③① D.④③②①
B
一天中不同时刻物体影子的长短和方向是不同的,在北半球(以冬季为例),一天中不同的时刻,影子的方向是按“正西→西北→正北→东北→正东”的顺序变化的;影子的长短是从早晨到中午由长逐渐变短,从中午到下午由短逐渐变长的.
影子的长短和方向的变化规律
如图a,b,c,d是一物体在不同时刻阳光下的影子情况,按照时间的先后顺序正确的是( )
A.a-b-c-d B.a-c-b-d C.d-c-b-a D.d-b-c-a.
B
2. 太阳光影子的应用
例2 如图所示,已知AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影。
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长。
解(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影。
(2)∵AC∥DF,∴∠ACB=∠DFE,
∵∠ABC=∠DEF=90°,
∴ ABC∽ DEF,
∴AB/DE=BC/EF,∴5/DE=3/6,
∴DE=10m.
F
同一时刻的平行投影中,(1)物体与影子上的对应点的连线互相平行;(2)物高与影长的比相等.
平等投影的规律
如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在相同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为6米,留在墙上的影高为2米,求旗杆的高度.
解:过C作CE⊥AB于E,连接AC.
∵CD⊥BD,AB⊥BD,
∴∠EBD=∠CDB=∠CEB=90°,∴四边形CDBE为矩形,
∴BD=CE=6,CD=BE=2.
设AE=x米,则1:1.5=x:6,
解得:x=4.
故旗杆高AB=AE+BE=4+2=6(米).
3.正投影
例3 一个圆柱如图,已知该圆柱的正投影是边长为4 cm的正方形,求圆柱的体积和表面积.
解:因为圆柱的正投影是边长为4cm的正方形,
所以圆柱的底面半径为2cm,高为4cm.
因此圆柱的两个底面的面积之和为:2×π×2 =8π(平方厘米)
圆柱的侧面面积为:4π×4=16π(平方厘米)
所以圆柱的表面积为S=24π(平方厘米).
圆柱的体积为:V=π×2 ×4=16π(立方厘米)
(1)物体的正投影可看作是从观察方向看到的物体的最大截面图形;
(2)正投影计算的关键是找准物体与其正投影之间的对应关系,然后根据图形的相关计算公式进行计算.
方法总结
如图,从左面看圆柱,则图中圆柱的投影是( )
A.圆 B.矩形 C.梯形 D.圆柱
B
兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,求树的高度.
解:如图,
设树的高度为AB,BD为落在地面的影长,CE为落在台阶上的影长,CD为台阶高
延长EC交AB于F,则四边形BDCF是矩形,
从而FC=BD=4.4,BF=CD=0.3,
所以EF=4.4+0.2=4.6,
则 AF/1= 4.6/0.4
解得AF=11.5,AB=AF+FB=11.5+0.3=11.8(米).
所以树的高度AB为11.8米.
故答案为:11.8米。
(中考. 伊春)在阳光的照射下,一块三角板的投影不会是( D )
A.线段 B,与原三角形全等的三角形 C.变形的三角形 D.点
【分析】 将一个三角板放在太阳光下,当它与阳光平行时,它所形成的投影是一条线段:当它与阳光成一定角度但不垂直时,它所形威的投影是三角形.
【解答】 解:根据太阳高度角不同,所形成的投影也不同,当三角板与阳光平行时,所形成的投影为一条线,当它与阳光形成一定角度但不垂直时,它所形成的投影是三角形,不可能是一个点,故选: D,
1.在同一时刻的阳光下,小明的影子比小强的影子长,那么在另一时刻(位置不变),则( )
A.小明的影子比小强的影子长
B.小明的影子比小强的影子短
C.两个人的影子一样长
D.无法判断谁的影子长
解析:因为阳光的光线是平行的,由条件可知小明的身高比小强的身高高,所以在另一时刻小明的影子也比小强的影子长.
A
2.在同一时刻,两根长度不等的竿子置于阳光之下,但它们的影子相等,那么这两根竿子的相对位置是( )
A.都垂直于地面 B.平行斜插在地上
C.不平行斜插在地上 D.都倒在地上
C
3.在阳光下同一时刻,身高1.4 m的小强影长1 m,旗杆影长15 m,则旗杆的高为____m.
4.如图,小明在A时刻测得某树的影长为2 m,在B时刻又测得该树的影长为8 m,若两次日照的光线互相垂直,则树的高度为____m.
21
4
5.某数学课外实验小组想利用树影测量树高.阳光下,他们在同一时刻测得一身高为1.5 m的同学影长为1.35 m,因为大树靠近一幢建筑物,影子不全在地面上(如图),他们测得地面部分的影长BC=3.6 m,墙上影长CD=1.8 m,则树高AB为____m.
5.8
6.已知:如图,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻,AB在阳光下的投影BC=4 m.
(1)请你在图中画出此时DE在阳光下的投影,并简述画图步骤;
(2)在测量AB的投影长时,同时测出DE在阳光下的投影长为6 m,请你计算DE的长.
解:(1)如图:
作法:连接AC,过点D作DF∥AC,交直线BE于点F,则EF就是DE的投影.
(2)由(1)知DF∥AC,∴∠ACB=∠DFE.
又∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF.
∴AB/DE=BC/EF,∴5/DE=4/6,
∴DE=7.5(m).
平行投影
平行投影与中心投影的关系
正投影
平行投影的特点
平行投影的作图
利用平行投影与正投影的特点解决实际问题
平行投影
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
