【原创精品】人教版数学九年级下册 29.2.2 《直棱柱的三视图》课件 (共27张PPT)
文档属性
| 名称 | 【原创精品】人教版数学九年级下册 29.2.2 《直棱柱的三视图》课件 (共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览





文档简介
(共27张PPT)
29.2.2 直棱柱的三视图
人教版九年级下册
第二十九章 投影与视图
1.会画几何体的三视图.
2.会根据三视图确定几何体.
3.能根据三视图的知识计算面积或体积.
重点:画简单几何体的三视图.
难点:三视图想象几何体.
学习目标
重点难点
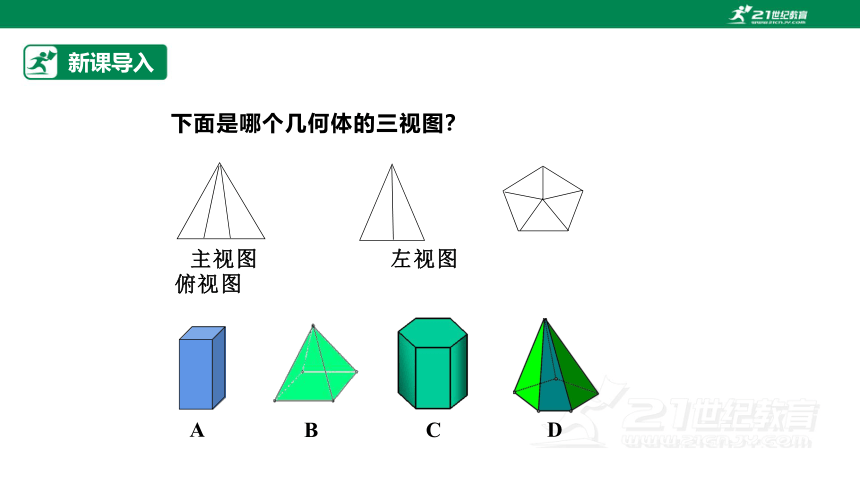
A
C
B
D
下面是哪个几何体的三视图?
主视图 左视图 俯视图
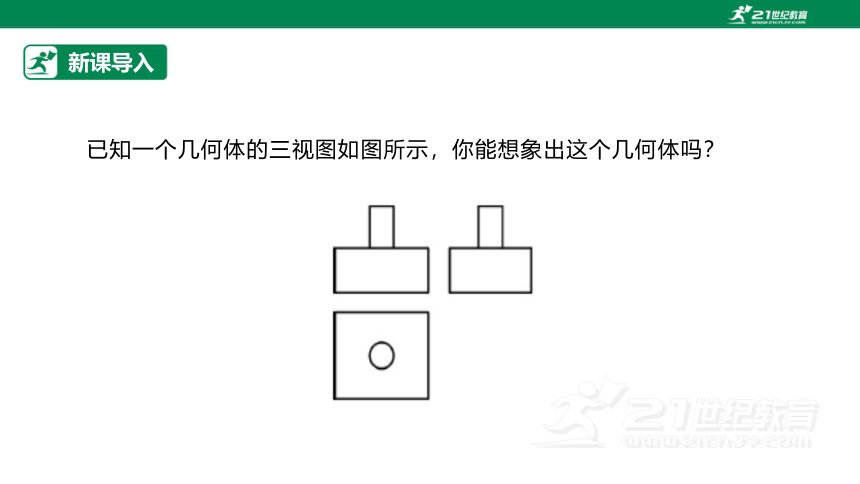
已知一个几何体的三视图如图所示,你能想象出这个几何体吗?
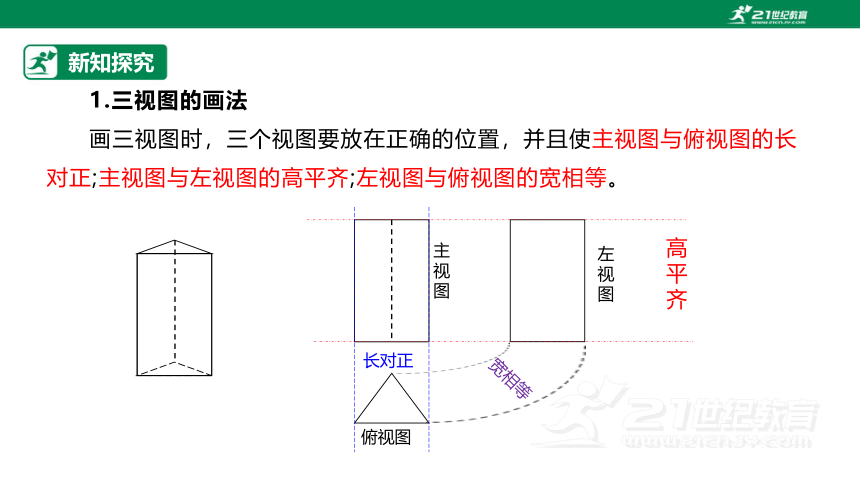
1.三视图的画法
画三视图时,三个视图要放在正确的位置,并且使主视图与俯视图的长对正;主视图与左视图的高平齐;左视图与俯视图的宽相等。
主视图
左视图
俯视图
高平齐
长对正
宽相等
2. 画三视图的规定:
(1)看得见部分的轮廓线画成实线,看不见部分的轮廓线画成虚线;
(2)若看得见的轮廓线与看不见的轮廓线重叠,则虚线不需画出;
(3)虚线也是反映物体形状的重要部分,必须按其位置画好.
3.画三视图的一般步骤总结为一定二画三原则,
(1)确定视图方向;
(2)画出能反映物体真实形状的一个视图;
(3)运用“长对正,高平齐,宽相等”的原则画出其他视图.
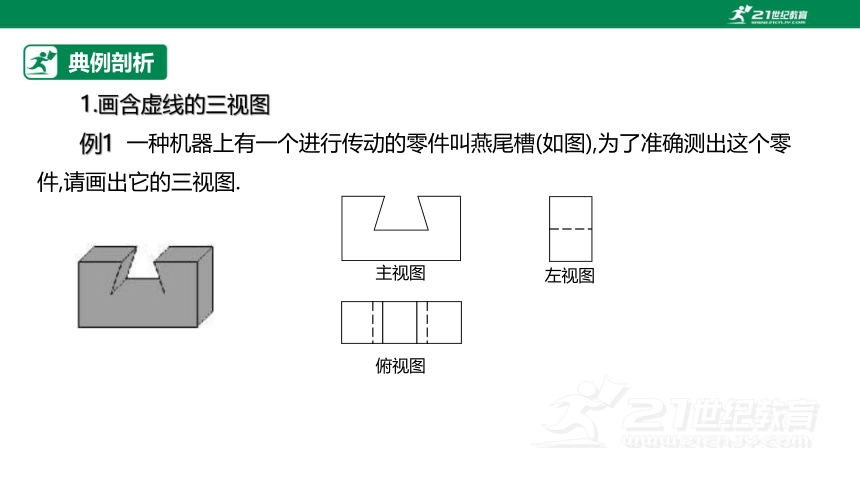
1.画含虚线的三视图
例1 一种机器上有一个进行传动的零件叫燕尾槽(如图),为了准确测出这个零件,请画出它的三视图.
主视图
俯视图
左视图
这个燕尾槽朝前的一个面与主视图投影面平行,所以这个燕尾槽的主视图与前面的面的大小、形状完全相同同理,可以得到其左视图和俯视图,按照“长对正、高平齐、宽相等”的原则画出三视图并放在相应的位置上.
燕尾槽画法
如图,请画出此几何体的三视图.
主视图
左视图
俯视图
2. 利用三视图与立体图形之间的关系判断几何体的名称
例2 某几何体的三视图如图所示则该几何体是( )
A.圆柱 B.三棱柱 C.长方体 D.四棱锥
C
方法总结
由三视图想象儿何体:
(1)方法:由三视图想象立体图形时,要先分别根据主视图、俯视图、左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
(2)过程:由三视图想象几何体形状,可通过以下途径进行分析:①根据主视图、俯视图、左视图想象几何体的前面、上面和左侧面的形状;②根据实线和虚线想象几何体看得见部分和看不见部分的轮廓线;③熟记一些简单的几何体的三视图会对复杂几何体的想象有帮助;④利用由几何体画三视图与由三视图画几何体的互逆过程,反复练习,不断总结方法.
一个几何体的三视图如图所示,则这个几何体是( )
D
3.利用三视图确定立体图形的面积或体积
例3 如图,是-个几何体的三视图,求这个几何体的侧面积和体积.
解:根据三视图可知,该几何体是正三棱柱,且底边长为2cm ,侧棱长为3cm,
则这个几何体的侧面积为
(3×2) ×3=6×3=18( cm ),
它的体积为
×2×√3 ×3 =3√3 ( cm ).
(1)根据三视图确定立体图形的形状;
(2)根据三视图标注的数据计算出立体图形的相关数据;
(3)根据立体图形的表面积或体积公式进行计算.
根据三视图求表面积或体积
如图是一个几何体的三视图,根据图中标注的数据可求得这个几何体的体积为( )
A.24π B.34π C.36π D.68π
A
如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要 个小立方块。
解:根据题中的三视图可知,下图上的数字表示俯视图该位置上小正方体的个数.
故该几何体共有小立方块1+1+2+3+1+1+1= 10个,
根据图形形状可知,要搭成一个4×4×4的大正方体,
那么至少还需要小立方块4×4×4-10=54个.
54
(2021 江西省)如图,几何体的主视图是( )
【分析】根据简单组合体的三视图的画法得出该组合体的主视图即可.
【解答】解:从正面看该组合体,长方体的主视图为长方形,圆柱体的主视图是长方形,
因此选项C中的图形符合题意,
故选:C.
C
1.如图是某几何体的三种视图,根据图中所标的数据求得该几何体的体积为( )
A.236π B.136π C.132π D.120π
B
2.一个几何体由n个大小相同的小正方体搭成,其左视图、俯视图如图所示,则n的值最小是( )
A.5 B.7 C.9 D.10
B
3.由一些大小相同的小正方体搭成的几何体的俯视图如下图所示,其中正方形中的数字表示该位置上的小正方体的个数,则该几何体的主视图是( )
C
4.如图是一个几何体的三视图,求这个几何体的侧面积.
解: 根据三种视图判断,该几何体是正三棱柱,
底面边长为2 cm,侧棱长是3 cm,
所以侧面积是(3×2)×3=3×6=18(cm ).
5.如图是某种型号的正六角螺母毛坯的三视图,求它的侧面积.
解:根据三种视图判断,该几何体是正六棱柱
所以S侧面积=2×3×6=36(cm ).
6.如图是一个几何体的两种视图,求该几何体的体积.(π取3.14)
解:根据三视图可以确定该几何体圆柱体与长方体组成.
V=V圆柱+V长方体
=π×( ×20) +30×25×40
=40 048(cm ).
棱锥的三视
图
三视图的作法
三视图确定几何体
根据三视图计算几何体的表面积或体积
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
29.2.2 直棱柱的三视图
人教版九年级下册
第二十九章 投影与视图
1.会画几何体的三视图.
2.会根据三视图确定几何体.
3.能根据三视图的知识计算面积或体积.
重点:画简单几何体的三视图.
难点:三视图想象几何体.
学习目标
重点难点
A
C
B
D
下面是哪个几何体的三视图?
主视图 左视图 俯视图
已知一个几何体的三视图如图所示,你能想象出这个几何体吗?
1.三视图的画法
画三视图时,三个视图要放在正确的位置,并且使主视图与俯视图的长对正;主视图与左视图的高平齐;左视图与俯视图的宽相等。
主视图
左视图
俯视图
高平齐
长对正
宽相等
2. 画三视图的规定:
(1)看得见部分的轮廓线画成实线,看不见部分的轮廓线画成虚线;
(2)若看得见的轮廓线与看不见的轮廓线重叠,则虚线不需画出;
(3)虚线也是反映物体形状的重要部分,必须按其位置画好.
3.画三视图的一般步骤总结为一定二画三原则,
(1)确定视图方向;
(2)画出能反映物体真实形状的一个视图;
(3)运用“长对正,高平齐,宽相等”的原则画出其他视图.
1.画含虚线的三视图
例1 一种机器上有一个进行传动的零件叫燕尾槽(如图),为了准确测出这个零件,请画出它的三视图.
主视图
俯视图
左视图
这个燕尾槽朝前的一个面与主视图投影面平行,所以这个燕尾槽的主视图与前面的面的大小、形状完全相同同理,可以得到其左视图和俯视图,按照“长对正、高平齐、宽相等”的原则画出三视图并放在相应的位置上.
燕尾槽画法
如图,请画出此几何体的三视图.
主视图
左视图
俯视图
2. 利用三视图与立体图形之间的关系判断几何体的名称
例2 某几何体的三视图如图所示则该几何体是( )
A.圆柱 B.三棱柱 C.长方体 D.四棱锥
C
方法总结
由三视图想象儿何体:
(1)方法:由三视图想象立体图形时,要先分别根据主视图、俯视图、左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
(2)过程:由三视图想象几何体形状,可通过以下途径进行分析:①根据主视图、俯视图、左视图想象几何体的前面、上面和左侧面的形状;②根据实线和虚线想象几何体看得见部分和看不见部分的轮廓线;③熟记一些简单的几何体的三视图会对复杂几何体的想象有帮助;④利用由几何体画三视图与由三视图画几何体的互逆过程,反复练习,不断总结方法.
一个几何体的三视图如图所示,则这个几何体是( )
D
3.利用三视图确定立体图形的面积或体积
例3 如图,是-个几何体的三视图,求这个几何体的侧面积和体积.
解:根据三视图可知,该几何体是正三棱柱,且底边长为2cm ,侧棱长为3cm,
则这个几何体的侧面积为
(3×2) ×3=6×3=18( cm ),
它的体积为
×2×√3 ×3 =3√3 ( cm ).
(1)根据三视图确定立体图形的形状;
(2)根据三视图标注的数据计算出立体图形的相关数据;
(3)根据立体图形的表面积或体积公式进行计算.
根据三视图求表面积或体积
如图是一个几何体的三视图,根据图中标注的数据可求得这个几何体的体积为( )
A.24π B.34π C.36π D.68π
A
如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要 个小立方块。
解:根据题中的三视图可知,下图上的数字表示俯视图该位置上小正方体的个数.
故该几何体共有小立方块1+1+2+3+1+1+1= 10个,
根据图形形状可知,要搭成一个4×4×4的大正方体,
那么至少还需要小立方块4×4×4-10=54个.
54
(2021 江西省)如图,几何体的主视图是( )
【分析】根据简单组合体的三视图的画法得出该组合体的主视图即可.
【解答】解:从正面看该组合体,长方体的主视图为长方形,圆柱体的主视图是长方形,
因此选项C中的图形符合题意,
故选:C.
C
1.如图是某几何体的三种视图,根据图中所标的数据求得该几何体的体积为( )
A.236π B.136π C.132π D.120π
B
2.一个几何体由n个大小相同的小正方体搭成,其左视图、俯视图如图所示,则n的值最小是( )
A.5 B.7 C.9 D.10
B
3.由一些大小相同的小正方体搭成的几何体的俯视图如下图所示,其中正方形中的数字表示该位置上的小正方体的个数,则该几何体的主视图是( )
C
4.如图是一个几何体的三视图,求这个几何体的侧面积.
解: 根据三种视图判断,该几何体是正三棱柱,
底面边长为2 cm,侧棱长是3 cm,
所以侧面积是(3×2)×3=3×6=18(cm ).
5.如图是某种型号的正六角螺母毛坯的三视图,求它的侧面积.
解:根据三种视图判断,该几何体是正六棱柱
所以S侧面积=2×3×6=36(cm ).
6.如图是一个几何体的两种视图,求该几何体的体积.(π取3.14)
解:根据三视图可以确定该几何体圆柱体与长方体组成.
V=V圆柱+V长方体
=π×( ×20) +30×25×40
=40 048(cm ).
棱锥的三视
图
三视图的作法
三视图确定几何体
根据三视图计算几何体的表面积或体积
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
