【精品原创】人教版数学九年级下册 26.1.2.1 《反比例函数的图象和性质1》教案
文档属性
| 名称 | 【精品原创】人教版数学九年级下册 26.1.2.1 《反比例函数的图象和性质1》教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册
26.1.2 反比例函数的图象和性质1 教案
课题名 26.1.2 反比例函数的图象和性质1
教学目标 1. 进一步熟悉画函数图象的主要步骤.2. 会画反比例函数的图象.3. 能够用反比例函数的图象解决一些实际问题
教学重点 反比例函数的图象.
教学难点 双曲线的特征.
教学准备 教师准备:PPT学生准备:图象纸、错题本、习题本、课堂笔记
教学过程
教学流程 教师活动 学生活动 设计意图
新课导入 师提出2个问题:1、怎样作一次函数y=kx+b(k≠0)、正比例函数y=kx(k≠0)的图象.2、反比例函数的图象是否象前面所学的函数一样是直线呢?图象会与坐标轴相交吗,为什么? 回答:简单地说描点法分列表、描点和连线三个步骤。根据预习得知,反比例函数的图象不是直线,它是两条双曲线。 复习巩固,引入新课。
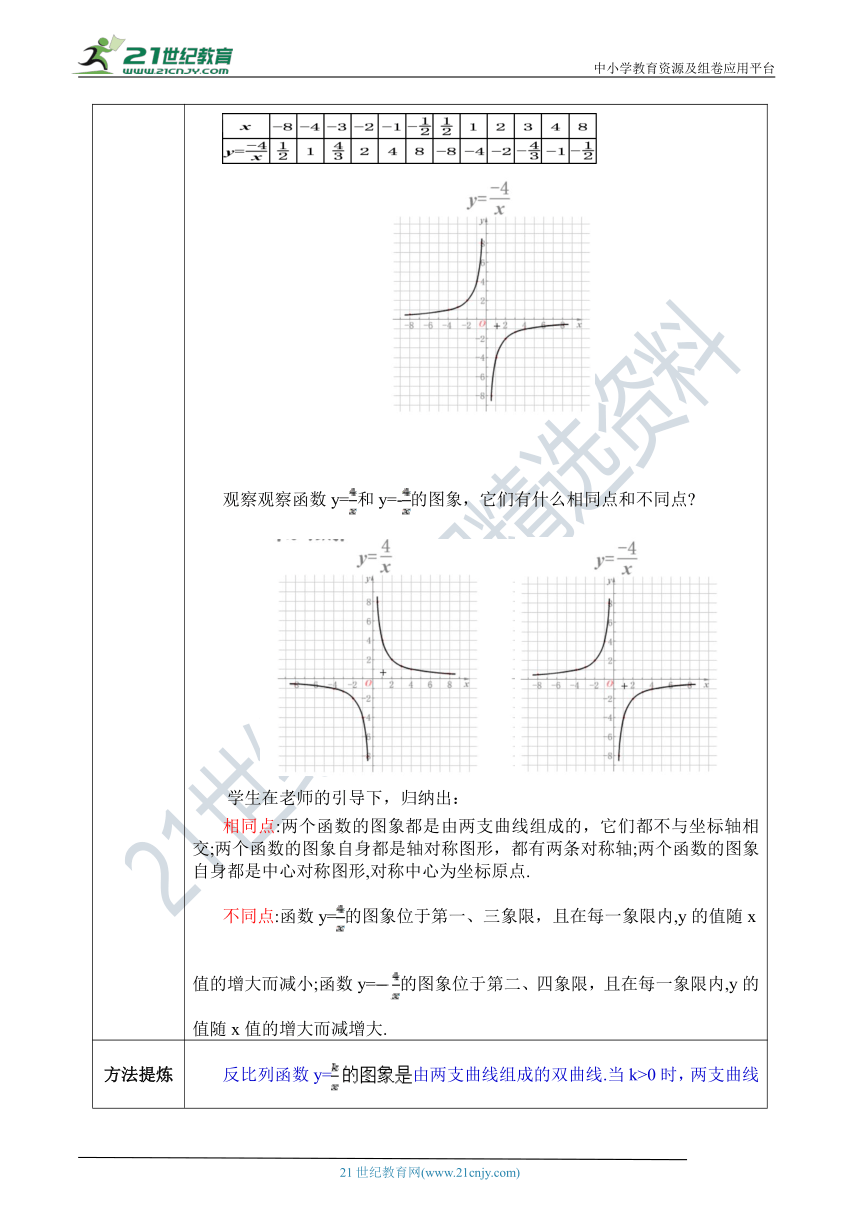
探究新知 师生互动:1.反比例函数图象的画法(描点法)(1)列表:反比例函数中自变量的取值范围是x≠0,为了便于计算,自变量通常取原点附近的数,如±1,±2,±3等,再求出对应y的值.(2 )描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.(3)连线:用光滑的曲线顺次连接各点并延伸,注意双曲线的两个分支是断开的,延伸部分有逐渐靠近坐标轴的趋势,但永远不与坐标轴相交.注意(1)列表时,自变量的取值可选取绝对值相等而符号相反的数值,这样既可简化计算,又便于描点;(2)反比例函数的图象不是直线,故不能用“两点法”作图,通常选取的点越多,画的图就越准确;(3)连线时不能连成折线,应该用光滑的曲线顺次连接各点,且画图时应注意其对称性及延伸性. 学生用图象专用纸或风格纸跟随老师的步骤画图象在下列直角坐标系中画反比例函数y=的图象.1.列表2.描点3.连线 直观表象帮助学生建立新知模型,形成脑图。培养学生素养,人书写习惯开始;学会用数学语言表达证明步骤。归纳总结探究的结果。
方法提炼 (1)一般地,画含数图象 ( http: / / www.21cnjy.com )时要在图象上标明函数的表达式.(2)画反比例函数的图象时 ( http: / / www.21cnjy.com ),要注意自变量x的取值范围为x≠0.在实际问题中,自变量要受到某些限制,此时画数图象表现为反比例函数图象的某一部分,且通常在第一象限.(3)因为反比例函数的图象关于原点成中心对称,所以在画反比例函数的图象时,只要画出它在一个象限内的分支,再利用图象的对称性即可画出另一个分支.
探究新知 2.反比例函数的图象在下列直角坐标系 ( http: / / www.21cnjy.com )中,画出反比例函数y=的图象. ( http: / / www.21cnjy.com / )观察观察函数y=和y=-的图象,它们有什么相同点和不同点 ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )学生在老师的引导下,归纳出:相同点:两个函数的图象都是由两支曲线组 ( http: / / www.21cnjy.com )成的,它们都不与坐标轴相交;两个函数的图象自身都是轴对称图形,都有两条对称轴;两个函数的图象自身都是中心对称图形,对称中心为坐标原点.不同点:函数y=的图象位于第一、三象限,且在每一象限内,y的值随x值的增大而减小;函数y=的图象位于第二、四象限,且在每一象限内,y的值随x值的增大而减增大.
方法提炼 反比列函数y=由两支曲线组成的双曲线.当k>0时,两支曲线分别位于第一、三象限内,在每个象限内,y随x的增大而减小;当k<0时,两支曲线分别位于第二、四象限内,在每个象限内,y随x的增大而增大.反比例函数的图象是中心对称图形,它的对称中心是坐标原点.反比例函数的图象是轴对称图形,对称轴是直线y=x和直线y=-x.
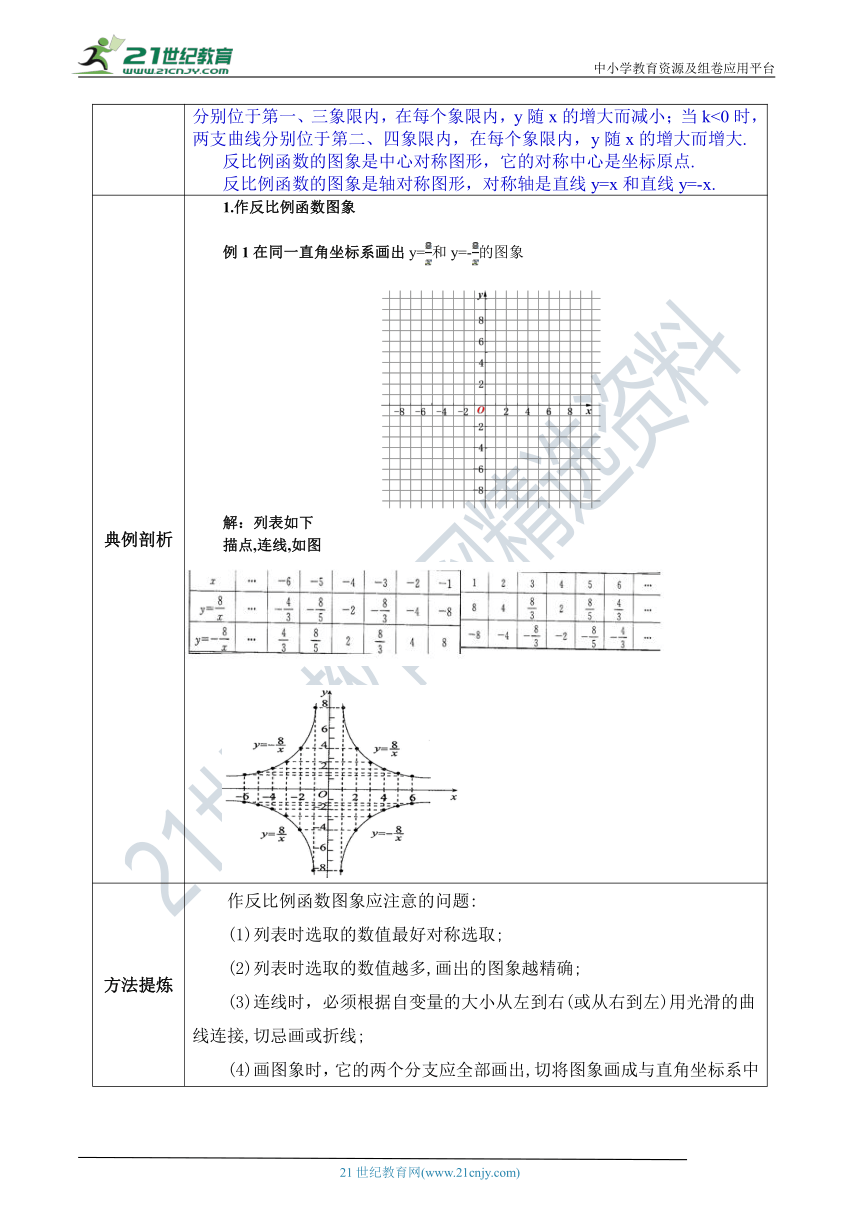
典例剖析 1.作反比例函数图象例1在同一直角坐标系画出y=和y=-的图象 ( http: / / www.21cnjy.com / )解:列表如下描点,连线,如图 ( http: / / www.21cnjy.com / )
方法提炼 作反比例函数图象应注意的问题:(1)列表时选取的数值最好对称选取;(2)列表时选取的数值越多,画出的图象越精确;(3)连线时,必须根据自变量的大小从左到右(或从右到左)用光滑的曲线连接,切忌画或折线;(4)画图象时,它的两个分支应全部画出,切将图象画成与直角坐标系中的坐标轴相交.
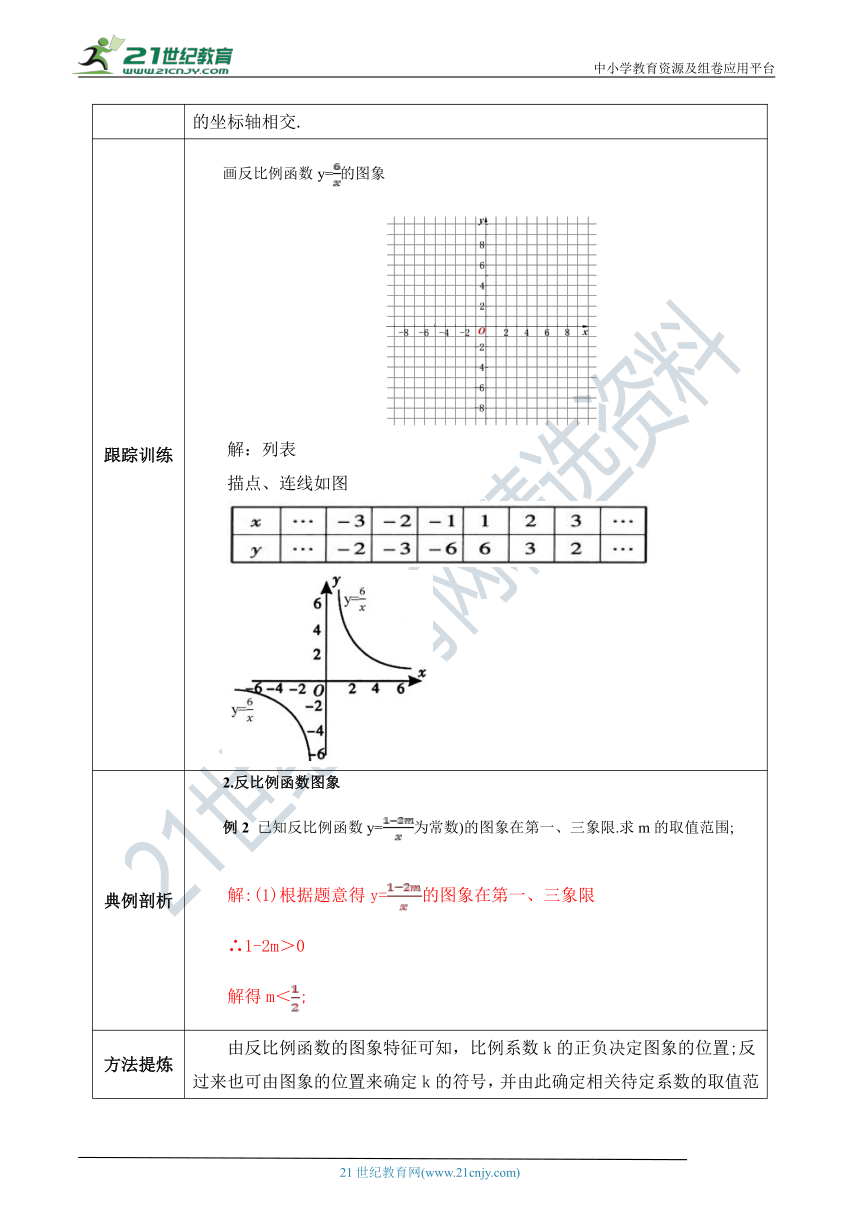
跟踪训练 画反比例函数y=的图象 ( http: / / www.21cnjy.com / )解:列表 描点、连线如图 ( http: / / www.21cnjy.com / )
典例剖析 2.反比例函数图象例2 已知反比例函数y=为常数)的图象在第一、三象限.求m的取值范围;解:(1)根据题意得y=的图象在第一、三象限∴1-2m>0解得m<;
方法提炼 由反比例函数的图象特征可知,比例系数k的正负决定图象的位置;反过来也可由图象的位置来确定k的符号,并由此确定相关待定系数的取值范围.
跟踪训练 如果k<0,那么函数y=(1﹣k)x与y=在同一坐标系中的图象可能是( )A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / )C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
拓展探究 已知反比例函数(k为常数,k≠0)(1)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围。(3)若其图象的一支位于第二象限,在这一 ( http: / / www.21cnjy.com )支上任取两点A(x ,y )、(x ,y ),当y >y 时,试比较x 与x 的大小。解:(1)在正比例函数y=x中,当y=2时,可知x=2,因此点P的坐标为(2,2),代入反比例函数的解析式中,可得,解得k=5.(2)因为y随x的增大而增大,∴k-1﹥0,解得k﹥1.(3)因为图象的一支处于第二象限,所以k-1<0,在每一支上,y随着x的增大而增大,因为y ﹥y ,所以x ﹥x .
链接中考 1.函数y=kx﹣3与 (k≠0)在同一坐标系内的图象可能是(B) ( http: / / www.21cnjy.com / )2.给出下列函数:①y=﹣3x+2; ( http: / / www.21cnjy.com )② ;③y=2x2;④y=3x,上述函数中符合条件“当x>1时,函数值y随自变量x增大而增大”的是( B )A.①③ B.③④ C.②④ D.②③
随堂检测 1.反比例函数y=-的图象位于( A )A.第二、四象限 B.第一、三象限 C.第一、二象限 D.第三、四象限2. 若点A(1,2),B(-2,-3)在直线y=kx+b上,则函数y=的图象位于( A )A.第一、三象限 B.第一、二象限 C.第二、四象限 D.第二、三象限3. 如图,在平面直角坐标系中,∠AO ( http: / / www.21cnjy.com )B=90°,∠OAB=30°,反比例函数y1=的图象经过点A,反比例函数y2=的图象经过点B,则下列关于m,n的关系正确的是( A )A.m=-3n B.m=-nC.m=-n D.m=n ( http: / / www.21cnjy.com / )4. 如图是三个反比例函数的图象的分支,其中k1,k2,k3的大小关系是k课堂小结 ( http: / / www.21cnjy.com / )
教学反思 本节课学生通过熟悉的描点法做出 ( http: / / www.21cnjy.com )反比例函数的图像,自主通过观察,探究,合作交流,总结反比例函数的图象和性质,从而更好的理解反比例函数,并且会应用函数图像解决一些问题,渗透数形结合的思想.注意时间的分配.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级下册
26.1.2 反比例函数的图象和性质1 教案
课题名 26.1.2 反比例函数的图象和性质1
教学目标 1. 进一步熟悉画函数图象的主要步骤.2. 会画反比例函数的图象.3. 能够用反比例函数的图象解决一些实际问题
教学重点 反比例函数的图象.
教学难点 双曲线的特征.
教学准备 教师准备:PPT学生准备:图象纸、错题本、习题本、课堂笔记
教学过程
教学流程 教师活动 学生活动 设计意图
新课导入 师提出2个问题:1、怎样作一次函数y=kx+b(k≠0)、正比例函数y=kx(k≠0)的图象.2、反比例函数的图象是否象前面所学的函数一样是直线呢?图象会与坐标轴相交吗,为什么? 回答:简单地说描点法分列表、描点和连线三个步骤。根据预习得知,反比例函数的图象不是直线,它是两条双曲线。 复习巩固,引入新课。
探究新知 师生互动:1.反比例函数图象的画法(描点法)(1)列表:反比例函数中自变量的取值范围是x≠0,为了便于计算,自变量通常取原点附近的数,如±1,±2,±3等,再求出对应y的值.(2 )描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.(3)连线:用光滑的曲线顺次连接各点并延伸,注意双曲线的两个分支是断开的,延伸部分有逐渐靠近坐标轴的趋势,但永远不与坐标轴相交.注意(1)列表时,自变量的取值可选取绝对值相等而符号相反的数值,这样既可简化计算,又便于描点;(2)反比例函数的图象不是直线,故不能用“两点法”作图,通常选取的点越多,画的图就越准确;(3)连线时不能连成折线,应该用光滑的曲线顺次连接各点,且画图时应注意其对称性及延伸性. 学生用图象专用纸或风格纸跟随老师的步骤画图象在下列直角坐标系中画反比例函数y=的图象.1.列表2.描点3.连线 直观表象帮助学生建立新知模型,形成脑图。培养学生素养,人书写习惯开始;学会用数学语言表达证明步骤。归纳总结探究的结果。
方法提炼 (1)一般地,画含数图象 ( http: / / www.21cnjy.com )时要在图象上标明函数的表达式.(2)画反比例函数的图象时 ( http: / / www.21cnjy.com ),要注意自变量x的取值范围为x≠0.在实际问题中,自变量要受到某些限制,此时画数图象表现为反比例函数图象的某一部分,且通常在第一象限.(3)因为反比例函数的图象关于原点成中心对称,所以在画反比例函数的图象时,只要画出它在一个象限内的分支,再利用图象的对称性即可画出另一个分支.
探究新知 2.反比例函数的图象在下列直角坐标系 ( http: / / www.21cnjy.com )中,画出反比例函数y=的图象. ( http: / / www.21cnjy.com / )观察观察函数y=和y=-的图象,它们有什么相同点和不同点 ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )学生在老师的引导下,归纳出:相同点:两个函数的图象都是由两支曲线组 ( http: / / www.21cnjy.com )成的,它们都不与坐标轴相交;两个函数的图象自身都是轴对称图形,都有两条对称轴;两个函数的图象自身都是中心对称图形,对称中心为坐标原点.不同点:函数y=的图象位于第一、三象限,且在每一象限内,y的值随x值的增大而减小;函数y=的图象位于第二、四象限,且在每一象限内,y的值随x值的增大而减增大.
方法提炼 反比列函数y=由两支曲线组成的双曲线.当k>0时,两支曲线分别位于第一、三象限内,在每个象限内,y随x的增大而减小;当k<0时,两支曲线分别位于第二、四象限内,在每个象限内,y随x的增大而增大.反比例函数的图象是中心对称图形,它的对称中心是坐标原点.反比例函数的图象是轴对称图形,对称轴是直线y=x和直线y=-x.
典例剖析 1.作反比例函数图象例1在同一直角坐标系画出y=和y=-的图象 ( http: / / www.21cnjy.com / )解:列表如下描点,连线,如图 ( http: / / www.21cnjy.com / )
方法提炼 作反比例函数图象应注意的问题:(1)列表时选取的数值最好对称选取;(2)列表时选取的数值越多,画出的图象越精确;(3)连线时,必须根据自变量的大小从左到右(或从右到左)用光滑的曲线连接,切忌画或折线;(4)画图象时,它的两个分支应全部画出,切将图象画成与直角坐标系中的坐标轴相交.
跟踪训练 画反比例函数y=的图象 ( http: / / www.21cnjy.com / )解:列表 描点、连线如图 ( http: / / www.21cnjy.com / )
典例剖析 2.反比例函数图象例2 已知反比例函数y=为常数)的图象在第一、三象限.求m的取值范围;解:(1)根据题意得y=的图象在第一、三象限∴1-2m>0解得m<;
方法提炼 由反比例函数的图象特征可知,比例系数k的正负决定图象的位置;反过来也可由图象的位置来确定k的符号,并由此确定相关待定系数的取值范围.
跟踪训练 如果k<0,那么函数y=(1﹣k)x与y=在同一坐标系中的图象可能是( )A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / )C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
拓展探究 已知反比例函数(k为常数,k≠0)(1)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围。(3)若其图象的一支位于第二象限,在这一 ( http: / / www.21cnjy.com )支上任取两点A(x ,y )、(x ,y ),当y >y 时,试比较x 与x 的大小。解:(1)在正比例函数y=x中,当y=2时,可知x=2,因此点P的坐标为(2,2),代入反比例函数的解析式中,可得,解得k=5.(2)因为y随x的增大而增大,∴k-1﹥0,解得k﹥1.(3)因为图象的一支处于第二象限,所以k-1<0,在每一支上,y随着x的增大而增大,因为y ﹥y ,所以x ﹥x .
链接中考 1.函数y=kx﹣3与 (k≠0)在同一坐标系内的图象可能是(B) ( http: / / www.21cnjy.com / )2.给出下列函数:①y=﹣3x+2; ( http: / / www.21cnjy.com )② ;③y=2x2;④y=3x,上述函数中符合条件“当x>1时,函数值y随自变量x增大而增大”的是( B )A.①③ B.③④ C.②④ D.②③
随堂检测 1.反比例函数y=-的图象位于( A )A.第二、四象限 B.第一、三象限 C.第一、二象限 D.第三、四象限2. 若点A(1,2),B(-2,-3)在直线y=kx+b上,则函数y=的图象位于( A )A.第一、三象限 B.第一、二象限 C.第二、四象限 D.第二、三象限3. 如图,在平面直角坐标系中,∠AO ( http: / / www.21cnjy.com )B=90°,∠OAB=30°,反比例函数y1=的图象经过点A,反比例函数y2=的图象经过点B,则下列关于m,n的关系正确的是( A )A.m=-3n B.m=-nC.m=-n D.m=n ( http: / / www.21cnjy.com / )4. 如图是三个反比例函数的图象的分支,其中k1,k2,k3的大小关系是k
教学反思 本节课学生通过熟悉的描点法做出 ( http: / / www.21cnjy.com )反比例函数的图像,自主通过观察,探究,合作交流,总结反比例函数的图象和性质,从而更好的理解反比例函数,并且会应用函数图像解决一些问题,渗透数形结合的思想.注意时间的分配.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
