【精品原创】人教版数学九年级下册 26.1.2.2《反比例函数的性质》教案
文档属性
| 名称 | 【精品原创】人教版数学九年级下册 26.1.2.2《反比例函数的性质》教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版数学七年级下册
26.1.2.2 反比例函数的性质2 教案
课题名 26.1.2.2 反比例函数的性质2
教学目标 1.掌握反比例函数的性质.2. 灵活应用反比例函数的性质进行有关计算.3. 理解反比例函数y=(k≠0)中比例系数k的几何意义
教学重点 掌握反比例函数的性质.
教学难点 比例系数的几何意义.
教学准备 教师准备:PPT学生准备:坐标纸、错题本、习题本、课堂笔记
教学过程
教学流程 教师活动 学生活动 设计意图
新课导入 师:按比例函数图象的有关基础知识是我们解决函数问题的基本依据,请大家解答以下几个题。师:我们知道一次函数的一些性质,反比例函数有什么性质呢? 反比例函数的图象是由两 ( http: / / www.21cnjy.com )支曲线组成的.当k>0时,两支曲线分别位于第________象限内,当k<0时,两支曲线分别位于第________象限内.如果反比例函数的图象过点A(1,2),那么这个反比例函数的图象在第________象限.已知点(-m,n)在反比例函数的图象上,则它的图象也一定经过点(m,____). 培养观察能力,并引入新课。
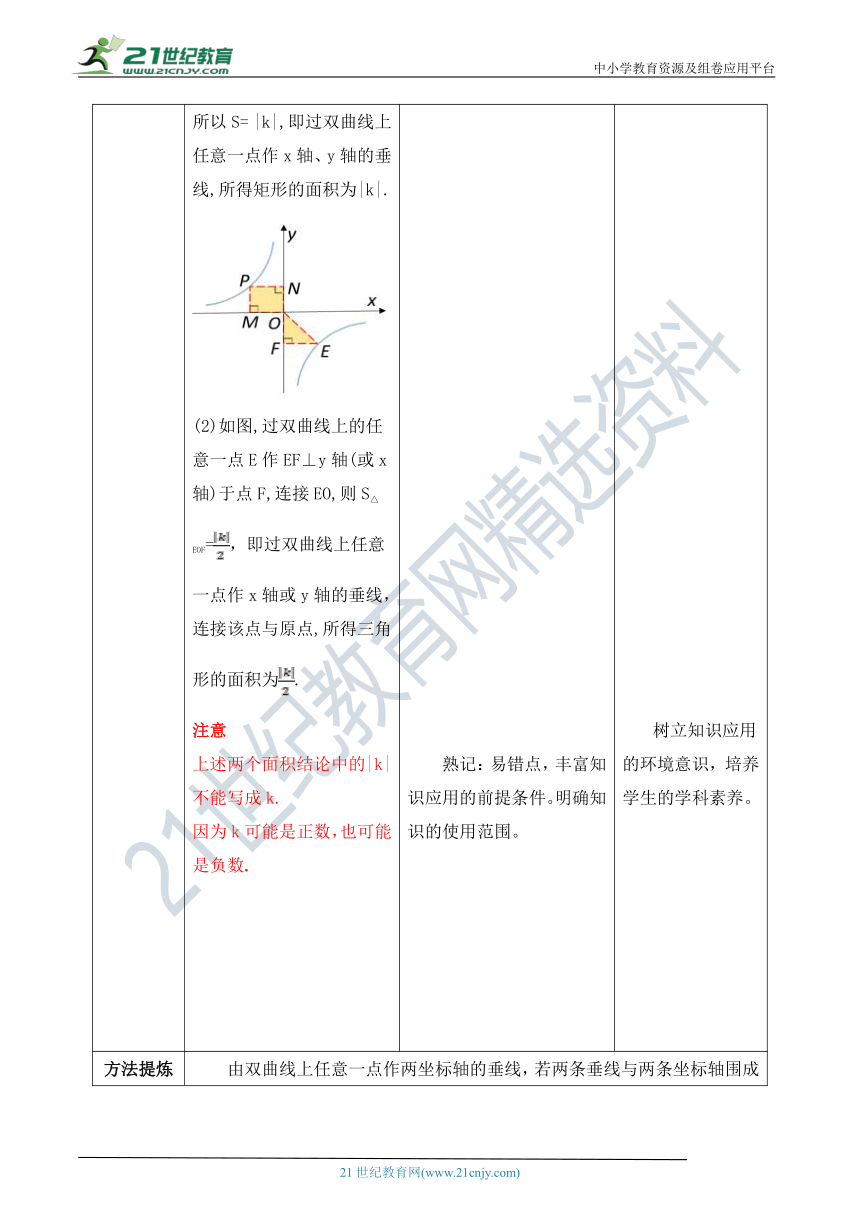
探究新知 师:首先探究1.反比例函数的性质观察反比例函数y=的图象当k>0,两支曲线分别在一、三象限,在每个象限内,y随x的增大而减小.当k<0,两支曲线分别在二、四象限,在每个象限内,y随x的增大而增大.2.反比例函数y=(k为常数,k≠0)中比例系数k的几何意义(1) 如图,过双曲线上任意点P(x,y) ( http: / / www.21cnjy.com )作PM⊥x轴于点M,PN⊥y轴于点N,所得矩形PMON的面积S=PM·PN=|y|·|x|= |xy|因为y= ,所以xy=k,所以S= |k|,即过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积为|k|. ( http: / / www.21cnjy.com / )(2)如图,过双曲线上的任意 ( http: / / www.21cnjy.com )一点E作EF⊥y轴(或x轴)于点F,连接EO,则S△EOF=,即过双曲线上任意一点作x轴或y轴的垂线,连接该点与原点,所得三角形的面积为.注意上述两个面积结论中的|k|不能写成k.因为k可能是正数,也可能是负数. 归纳出:(1)描述反比例函数的增减性时,必须指出“在每个象限...”不能笼统地说“当k>0时,y的值随x值的增大而减小...”.(2)比例系数k的符号决定了反比例函数图象的位置和函数的性质;反之,由反比例函数图象的位置及函数的增减性,也可以推断出比例系数k的符号.(3)反比例函数的图象既是中心对称图形,又是轴对称图形,它有两条对称轴,一条是直线y=x,另一条是直线y=-x,对称中心为坐标原点.(4)|k|的值越大,双曲线距离原点越远. 跟随老师探究第二个知识点。 熟记:易错点,丰富知识应用的前提条件。明确知识的使用范围。 明确探究范围,强调“函数”。直观表象帮助学生建立新知模型,形成脑图。培养学生数学学科素养,学会用数学语言表达证明步骤。归纳总结探究的结果。树立知识应用的环境意识,培养学生的学科素养。
方法提炼 由双曲线上任意一点作两坐标轴的垂线,若两条垂线与两条坐标轴围成的矩形面积为k(k>0),则此双曲线的函数表达式为y=±.当该点位于第一、三象限时,双曲线对应的函数表达式为y=;当该点位于第二、四象限时,双曲线对应的函数表达式为y=- ;当不能确定该点所在的象限时,双曲线的函数表达式为y=±.
典例剖析 1.反比例函数的性质例1(1)若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( D )A.y1方法提炼 比较反比例函数值的大小一般有三种方法:(1)直接把两个点的坐标代入函数表达式,求出相应的函数值,比较大小;(2)在函数图象上描出各点,再根据各点的位置高低,比较数的大小;(3)利用函数的增减性,比较数的大小。(4)画图象时,它的两个分支应全部画出,切将图象画成与直角坐标系中的坐标轴相交.
跟踪训练 反比例函数y=(2m-1)x|m|-2,当x>0时,y随x的增大而增大,则m=_-1_.
典例剖析 2.反比例函数系数的几何意义例2 如图:A,B是函数y=的图象上关于原点O对称的任意两点.AC平行于y轴,BC平行于x轴,求 ABC的面积.解:如图所示, 设A点坐标为(x、),则B点坐标为(-x,-), ∴C点坐标为(x,-), ∴S矩形OECD=x·|-|=1, ∵A、B为函数y=图象上两点, ∴S AOE=S BOD==,∴S ABC=S矩形OECD+ S AOE=S BOD =1++=2.
方法提炼 过反比例函数y=意一点,向两坐标轴作垂线段,所得矩形的面积等于|k|.在确定k的值时一定要注意图象所在的象限,从而舍去不合题意的值.
跟踪训练 如图,OABC为菱形,点C在x轴上,点A在直线y=x上,点B在y=(k>0)的图象上,若S菱形OABC=,求k的值.解: ∵直线y=x经过点A, ∴设A(a,a), ∴OA =2a , ∴AO=, ∵四边形ABCD是菱形, ∴AO=CO=CB=AB= , ∵菱形OABC的面积是, ∴a·a=, ∴a=1, ∴AB=, A(1,1)∴B(1+,1), 设反比例函数解析式为y=(k≠0), ∵B(1+,1)在反比例函数图象上, ∴k=(1+)=, 故k的值为.
典例剖析 3.反比例函数的综合运用例3 如图,在△ABC中,AB=AC,B ( http: / / www.21cnjy.com )C⊥x轴,垂足为D,边AB所在直线分别交x轴、y轴于点E、F,且AF=EF,反比例函数y=的图象经过A、C两点,已知点A(2,n).(1)求AB所在直线对应的函数表达式;(2)求点C的坐标.解: (1)把A(2,n)代入y=,得到n=6,作AH⊥OD于H.∴OH=2 , AH=6,∵OF∥AH,∴ EFO∽ EAH,∴EF:EA=FO:AH=EO:EH.∵EF=AF,∴EF:EA=FO:AH=EO:EH.=1:2∴EO=2, FO=3,∴E( -2 ,0) ,F(0,3) ,设直线AB的解析式为y= kx+b,则有,解得∴直线AB的解析式为y=x+3.(2 )作AG ⊥ BD于G .则四边形AGDH是矩形,∴DG=AH=6,设C(a,) ,则B(a, a+3),∴CD=, BG=a+3-6=a-3, GC=6 -,∵AB=AC , AG⊥BC , ∴.BG=CG ,a-3=6 -整理得: a - 6a+8=0 , a= 4或2(舍去),∴C的坐标为(4, 3 )
跟踪训练 如图,在平面直角坐标系中,菱形ABCD的顶点 ( http: / / www.21cnjy.com )A,B在反比例函数y=(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为,则k的值为( D )A. B. C.4 D.5
拓展探究 如图,已知点D在反比例函数y=的图象上,过点 D作DB⊥y轴轴,垂足为垂足B(0,3),直线 y=kx+b经过点 A(5,0),与y轴交于点C,且BD=OC,OC:OA=2:5.(1)求反比例函数y=和一次函数y=kx+b的表达式;(2)直接写出关于x的不等式>kx+b的解集.解:(1) ∵BD=OC,OC : OA=2 : 5,点A(5,0) ,点B(0,3),∴OA=5,OC= BD=2,OB=3,又∵点C在y轴负半轴,点D在第二象限,∴点C的坐标为(0,-2),点D的坐标为(-2,3).∴a=-6∴反比例函数表达式y=的图象上, 将A(5,0)、B(0,- 2)代入y=kx+b,得,解得 ∴一次函数的表达式为y=.(2)将y=代入y=-,整理得-2x+6=0∵ =-<0∴一次函数与反比例函数无交点.观察图形,可知:当x<0时,反比例函数图象在一次函数图象上方,∴不等式> kx+b的解集为x<0.
链接中考 (中考·黑龙江肇东) 如图,正方形AB ( http: / / www.21cnjy.com )CD 的两个顶点 B,D 在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点 0,已知 B (-1,1),则k的值是( )A.-5 B.-4 C.-3 D.-1【答案】D【解析】本题考查了待定系数法求反比例函数解析式,解: ∵点 B 在反比例函数 y=的图象上. B (-1. 1)。∴1= , ∴ k=-1,故选:D
随堂检测 1.已知反比例函数y=- ,下列结论中错误的是( A )A.图象在第二、四象限内 B.图象必经过(-2,4) C.当-18 D.y随x的增大而增大2. 如图,点P在反比例函数y=(k≠0)的图象上,PA⊥x轴于点A,△PAO的面积为2,则k的值为( C )A.1 B.2 C.4 D.6 ( http: / / www.21cnjy.com / )3已知反比例函数y=-,当-32时,02,(2)由函数图象知,当x>2时,0课堂小结 ( http: / / www.21cnjy.com / )
教学反思 本节课结合面积、函数等相关知识点去 ( http: / / www.21cnjy.com )拓展应用,从而更好的理解反比例函数,并且会应用函数图像解决一些问题,渗透数形结合的思想.课堂上充分留给学生动脑、动手、动口的机会,让每个学生都有进步的机会和展示自己的舞台.
m>
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学七年级下册
26.1.2.2 反比例函数的性质2 教案
课题名 26.1.2.2 反比例函数的性质2
教学目标 1.掌握反比例函数的性质.2. 灵活应用反比例函数的性质进行有关计算.3. 理解反比例函数y=(k≠0)中比例系数k的几何意义
教学重点 掌握反比例函数的性质.
教学难点 比例系数的几何意义.
教学准备 教师准备:PPT学生准备:坐标纸、错题本、习题本、课堂笔记
教学过程
教学流程 教师活动 学生活动 设计意图
新课导入 师:按比例函数图象的有关基础知识是我们解决函数问题的基本依据,请大家解答以下几个题。师:我们知道一次函数的一些性质,反比例函数有什么性质呢? 反比例函数的图象是由两 ( http: / / www.21cnjy.com )支曲线组成的.当k>0时,两支曲线分别位于第________象限内,当k<0时,两支曲线分别位于第________象限内.如果反比例函数的图象过点A(1,2),那么这个反比例函数的图象在第________象限.已知点(-m,n)在反比例函数的图象上,则它的图象也一定经过点(m,____). 培养观察能力,并引入新课。
探究新知 师:首先探究1.反比例函数的性质观察反比例函数y=的图象当k>0,两支曲线分别在一、三象限,在每个象限内,y随x的增大而减小.当k<0,两支曲线分别在二、四象限,在每个象限内,y随x的增大而增大.2.反比例函数y=(k为常数,k≠0)中比例系数k的几何意义(1) 如图,过双曲线上任意点P(x,y) ( http: / / www.21cnjy.com )作PM⊥x轴于点M,PN⊥y轴于点N,所得矩形PMON的面积S=PM·PN=|y|·|x|= |xy|因为y= ,所以xy=k,所以S= |k|,即过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积为|k|. ( http: / / www.21cnjy.com / )(2)如图,过双曲线上的任意 ( http: / / www.21cnjy.com )一点E作EF⊥y轴(或x轴)于点F,连接EO,则S△EOF=,即过双曲线上任意一点作x轴或y轴的垂线,连接该点与原点,所得三角形的面积为.注意上述两个面积结论中的|k|不能写成k.因为k可能是正数,也可能是负数. 归纳出:(1)描述反比例函数的增减性时,必须指出“在每个象限...”不能笼统地说“当k>0时,y的值随x值的增大而减小...”.(2)比例系数k的符号决定了反比例函数图象的位置和函数的性质;反之,由反比例函数图象的位置及函数的增减性,也可以推断出比例系数k的符号.(3)反比例函数的图象既是中心对称图形,又是轴对称图形,它有两条对称轴,一条是直线y=x,另一条是直线y=-x,对称中心为坐标原点.(4)|k|的值越大,双曲线距离原点越远. 跟随老师探究第二个知识点。 熟记:易错点,丰富知识应用的前提条件。明确知识的使用范围。 明确探究范围,强调“函数”。直观表象帮助学生建立新知模型,形成脑图。培养学生数学学科素养,学会用数学语言表达证明步骤。归纳总结探究的结果。树立知识应用的环境意识,培养学生的学科素养。
方法提炼 由双曲线上任意一点作两坐标轴的垂线,若两条垂线与两条坐标轴围成的矩形面积为k(k>0),则此双曲线的函数表达式为y=±.当该点位于第一、三象限时,双曲线对应的函数表达式为y=;当该点位于第二、四象限时,双曲线对应的函数表达式为y=- ;当不能确定该点所在的象限时,双曲线的函数表达式为y=±.
典例剖析 1.反比例函数的性质例1(1)若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( D )A.y1
跟踪训练 反比例函数y=(2m-1)x|m|-2,当x>0时,y随x的增大而增大,则m=_-1_.
典例剖析 2.反比例函数系数的几何意义例2 如图:A,B是函数y=的图象上关于原点O对称的任意两点.AC平行于y轴,BC平行于x轴,求 ABC的面积.解:如图所示, 设A点坐标为(x、),则B点坐标为(-x,-), ∴C点坐标为(x,-), ∴S矩形OECD=x·|-|=1, ∵A、B为函数y=图象上两点, ∴S AOE=S BOD==,∴S ABC=S矩形OECD+ S AOE=S BOD =1++=2.
方法提炼 过反比例函数y=意一点,向两坐标轴作垂线段,所得矩形的面积等于|k|.在确定k的值时一定要注意图象所在的象限,从而舍去不合题意的值.
跟踪训练 如图,OABC为菱形,点C在x轴上,点A在直线y=x上,点B在y=(k>0)的图象上,若S菱形OABC=,求k的值.解: ∵直线y=x经过点A, ∴设A(a,a), ∴OA =2a , ∴AO=, ∵四边形ABCD是菱形, ∴AO=CO=CB=AB= , ∵菱形OABC的面积是, ∴a·a=, ∴a=1, ∴AB=, A(1,1)∴B(1+,1), 设反比例函数解析式为y=(k≠0), ∵B(1+,1)在反比例函数图象上, ∴k=(1+)=, 故k的值为.
典例剖析 3.反比例函数的综合运用例3 如图,在△ABC中,AB=AC,B ( http: / / www.21cnjy.com )C⊥x轴,垂足为D,边AB所在直线分别交x轴、y轴于点E、F,且AF=EF,反比例函数y=的图象经过A、C两点,已知点A(2,n).(1)求AB所在直线对应的函数表达式;(2)求点C的坐标.解: (1)把A(2,n)代入y=,得到n=6,作AH⊥OD于H.∴OH=2 , AH=6,∵OF∥AH,∴ EFO∽ EAH,∴EF:EA=FO:AH=EO:EH.∵EF=AF,∴EF:EA=FO:AH=EO:EH.=1:2∴EO=2, FO=3,∴E( -2 ,0) ,F(0,3) ,设直线AB的解析式为y= kx+b,则有,解得∴直线AB的解析式为y=x+3.(2 )作AG ⊥ BD于G .则四边形AGDH是矩形,∴DG=AH=6,设C(a,) ,则B(a, a+3),∴CD=, BG=a+3-6=a-3, GC=6 -,∵AB=AC , AG⊥BC , ∴.BG=CG ,a-3=6 -整理得: a - 6a+8=0 , a= 4或2(舍去),∴C的坐标为(4, 3 )
跟踪训练 如图,在平面直角坐标系中,菱形ABCD的顶点 ( http: / / www.21cnjy.com )A,B在反比例函数y=(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为,则k的值为( D )A. B. C.4 D.5
拓展探究 如图,已知点D在反比例函数y=的图象上,过点 D作DB⊥y轴轴,垂足为垂足B(0,3),直线 y=kx+b经过点 A(5,0),与y轴交于点C,且BD=OC,OC:OA=2:5.(1)求反比例函数y=和一次函数y=kx+b的表达式;(2)直接写出关于x的不等式>kx+b的解集.解:(1) ∵BD=OC,OC : OA=2 : 5,点A(5,0) ,点B(0,3),∴OA=5,OC= BD=2,OB=3,又∵点C在y轴负半轴,点D在第二象限,∴点C的坐标为(0,-2),点D的坐标为(-2,3).∴a=-6∴反比例函数表达式y=的图象上, 将A(5,0)、B(0,- 2)代入y=kx+b,得,解得 ∴一次函数的表达式为y=.(2)将y=代入y=-,整理得-2x+6=0∵ =-<0∴一次函数与反比例函数无交点.观察图形,可知:当x<0时,反比例函数图象在一次函数图象上方,∴不等式> kx+b的解集为x<0.
链接中考 (中考·黑龙江肇东) 如图,正方形AB ( http: / / www.21cnjy.com )CD 的两个顶点 B,D 在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点 0,已知 B (-1,1),则k的值是( )A.-5 B.-4 C.-3 D.-1【答案】D【解析】本题考查了待定系数法求反比例函数解析式,解: ∵点 B 在反比例函数 y=的图象上. B (-1. 1)。∴1= , ∴ k=-1,故选:D
随堂检测 1.已知反比例函数y=- ,下列结论中错误的是( A )A.图象在第二、四象限内 B.图象必经过(-2,4) C.当-1
教学反思 本节课结合面积、函数等相关知识点去 ( http: / / www.21cnjy.com )拓展应用,从而更好的理解反比例函数,并且会应用函数图像解决一些问题,渗透数形结合的思想.课堂上充分留给学生动脑、动手、动口的机会,让每个学生都有进步的机会和展示自己的舞台.
m>
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
