【精品原创】人教版数学九年级下册 27.2.1.1 《相似三角形的判定1》教案
文档属性
| 名称 | 【精品原创】人教版数学九年级下册 27.2.1.1 《相似三角形的判定1》教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学七年级下册
27.2.1.1 相似三角形的判定1 教案
课题名 27.2.1.1 相似三角形的判定1
教学目标 1、平行线分线段成比例定理及其推论。2、会应用平行线分线段成比例定理写比例式、计算。3、经历探究平行线分线段成比例定理的过程,培养分析归纳能力.
教学重点 平行线分线段成比例定理及其推论
教学难点 灵活运用平行线分线段成比例定理及其推论解决有关问题
教学准备 教师准备:PPT学生准备:坐标纸、错题本、习题本、课堂笔记
教学过程
教学流程 教师活动 学生活动 设计意图
新课导入 如图,在作业本上任意画一条直线m与相邻 ( http: / / www.21cnjy.com )的三条平行线交于A、B、C三点,得到两条线段AB、BC,再任意画一条直线n与这组平行线相交,得到两条线段DE和EF,我们能发现什么呢? 按要求画图: ( http: / / www.21cnjy.com / )得出: 参与知识的形成过程,并引入新课。
探究新知 师:我们继续探究上刚才的操作。选择作业本上不相邻的三条平行线,任意画两 ( http: / / www.21cnjy.com )条直线m、n与它们相交。如果m、n这两条直线平行,观察并思考这时所得的AD、DB、FE、EC这四条线段的长度有什么关系;如果m、n这两条直线不平行,你再观察一下,也可以量一量,看看它们是否存在类似的关系?我们可以发现,当两条直线与一组平行线相交时,所截得的线段存在一定的比例关系: ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )结论:两条直线被一组平行线所截,所得的对应线段成比例.(简称“平行线分线段成比例”) 培养学生数学学科素养,学会用数学语言表达证明步骤。归纳总结探究的结果。直观表象帮助学生建立新知模型,形成脑图。
方法提炼 几何语言:∵//// ∴(平行线分线段成比例)
探究新知 如图,当图中的点A与点F重合时,就形成一个三角形的特殊情形,此时,AD、DB、AE、EC这四条线段之间会有怎样的关系呢?在△ABC中,DE//BC,过点A作DE的平行线,∴, ∴=如图,当直线m,n相交于第二条平行线上某点时,是否也有类似的成比例线段呢?
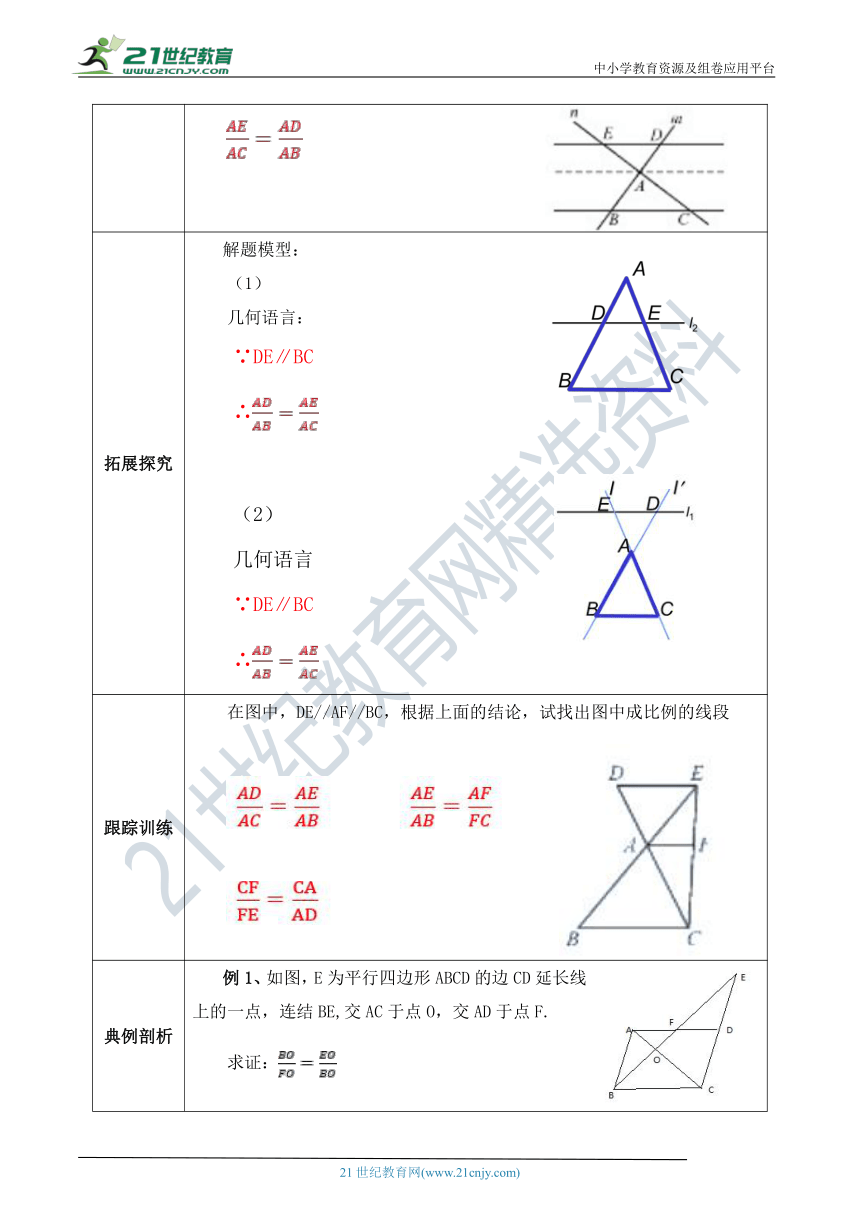
拓展探究 解题模型:(1)几何语言:∵DE∥BC∴(2)几何语言∵DE∥BC∴
跟踪训练 在图中,DE//AF//BC,根据上面的结论,试找出图中成比例的线段
典例剖析 例1、如图,E为平行四边形ABCD的边CD延长线上的一点,连结BE,交AC于点O,交AD于点F.求证: ( http: / / www.21cnjy.com / )
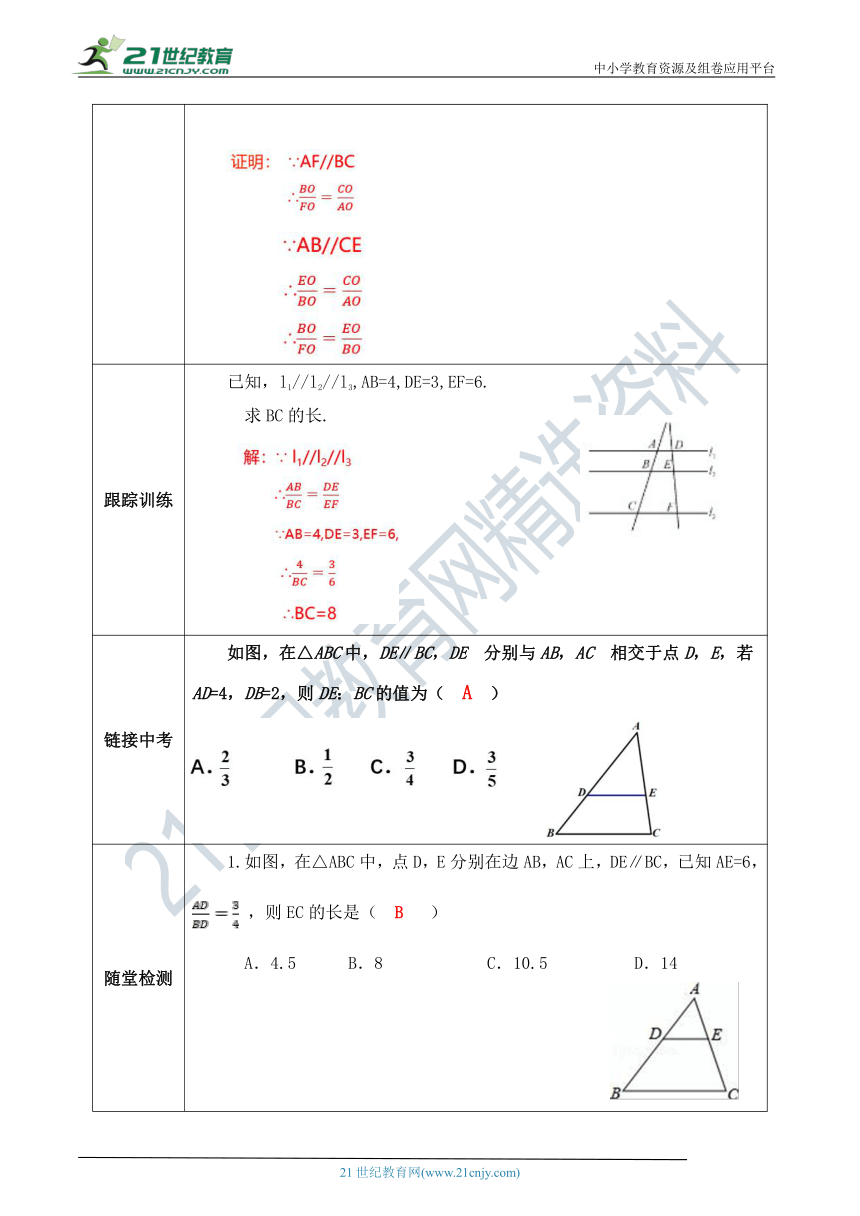
跟踪训练 已知,l1//l2//l3,AB=4,DE=3,EF=6.求BC的长. ( http: / / www.21cnjy.com / )
链接中考 如图,在△ABC中,DE∥BC,DE 分别与AB,AC 相交于点D,E,若AD=4,DB=2,则DE:BC的值为( A )
随堂检测 1.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6, ,则EC的长是( B ) A.4.5 B.8 C.10.5 D.14 2.如图,直线l1∥l2∥l3,直线A ( http: / / www.21cnjy.com )C分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则的值为( D )A. B.2 C. D. 3.如图,AD∥BE∥CF,直线l1,l2与 ( http: / / www.21cnjy.com )这三条平行线分别交于点A,B,C和点D,E,F,=,DE=6,则EF= 9. 4.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .5.如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2,BC=8.求BF和CF的长。解:∵DE//BC∴ ∵DF//AC∴∴,即CF=∴BF=8-6.如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,求EF.解:∵AB∥CD,∴ ,∴ ,∵AB∥EF,∴ ,即 ,解得EF=4cm.
课堂小结 ( http: / / www.21cnjy.com / )
教学反思 关于平行线分线段成比例定理,学 ( http: / / www.21cnjy.com )生没有足够体验,很难达到对定理的理解,进而影响了后续知识的掌握.所有的新知识,都要通过自身“再创造”,纳入到自己的认知结构中,成为有效而能发展的知识,优化和发展了数学认知结构.因此在教学过程中,要让学生经历“观察——猜想——归纳——验证”等一系列的数学活动,不断体会数形结合和从特殊到一般的数学思想方法.要给学生充足的研讨时间,化未知为已知,从而不断完善学生的认知体系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学七年级下册
27.2.1.1 相似三角形的判定1 教案
课题名 27.2.1.1 相似三角形的判定1
教学目标 1、平行线分线段成比例定理及其推论。2、会应用平行线分线段成比例定理写比例式、计算。3、经历探究平行线分线段成比例定理的过程,培养分析归纳能力.
教学重点 平行线分线段成比例定理及其推论
教学难点 灵活运用平行线分线段成比例定理及其推论解决有关问题
教学准备 教师准备:PPT学生准备:坐标纸、错题本、习题本、课堂笔记
教学过程
教学流程 教师活动 学生活动 设计意图
新课导入 如图,在作业本上任意画一条直线m与相邻 ( http: / / www.21cnjy.com )的三条平行线交于A、B、C三点,得到两条线段AB、BC,再任意画一条直线n与这组平行线相交,得到两条线段DE和EF,我们能发现什么呢? 按要求画图: ( http: / / www.21cnjy.com / )得出: 参与知识的形成过程,并引入新课。
探究新知 师:我们继续探究上刚才的操作。选择作业本上不相邻的三条平行线,任意画两 ( http: / / www.21cnjy.com )条直线m、n与它们相交。如果m、n这两条直线平行,观察并思考这时所得的AD、DB、FE、EC这四条线段的长度有什么关系;如果m、n这两条直线不平行,你再观察一下,也可以量一量,看看它们是否存在类似的关系?我们可以发现,当两条直线与一组平行线相交时,所截得的线段存在一定的比例关系: ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )结论:两条直线被一组平行线所截,所得的对应线段成比例.(简称“平行线分线段成比例”) 培养学生数学学科素养,学会用数学语言表达证明步骤。归纳总结探究的结果。直观表象帮助学生建立新知模型,形成脑图。
方法提炼 几何语言:∵//// ∴(平行线分线段成比例)
探究新知 如图,当图中的点A与点F重合时,就形成一个三角形的特殊情形,此时,AD、DB、AE、EC这四条线段之间会有怎样的关系呢?在△ABC中,DE//BC,过点A作DE的平行线,∴, ∴=如图,当直线m,n相交于第二条平行线上某点时,是否也有类似的成比例线段呢?
拓展探究 解题模型:(1)几何语言:∵DE∥BC∴(2)几何语言∵DE∥BC∴
跟踪训练 在图中,DE//AF//BC,根据上面的结论,试找出图中成比例的线段
典例剖析 例1、如图,E为平行四边形ABCD的边CD延长线上的一点,连结BE,交AC于点O,交AD于点F.求证: ( http: / / www.21cnjy.com / )
跟踪训练 已知,l1//l2//l3,AB=4,DE=3,EF=6.求BC的长. ( http: / / www.21cnjy.com / )
链接中考 如图,在△ABC中,DE∥BC,DE 分别与AB,AC 相交于点D,E,若AD=4,DB=2,则DE:BC的值为( A )
随堂检测 1.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6, ,则EC的长是( B ) A.4.5 B.8 C.10.5 D.14 2.如图,直线l1∥l2∥l3,直线A ( http: / / www.21cnjy.com )C分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则的值为( D )A. B.2 C. D. 3.如图,AD∥BE∥CF,直线l1,l2与 ( http: / / www.21cnjy.com )这三条平行线分别交于点A,B,C和点D,E,F,=,DE=6,则EF= 9. 4.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .5.如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2,BC=8.求BF和CF的长。解:∵DE//BC∴ ∵DF//AC∴∴,即CF=∴BF=8-6.如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,求EF.解:∵AB∥CD,∴ ,∴ ,∵AB∥EF,∴ ,即 ,解得EF=4cm.
课堂小结 ( http: / / www.21cnjy.com / )
教学反思 关于平行线分线段成比例定理,学 ( http: / / www.21cnjy.com )生没有足够体验,很难达到对定理的理解,进而影响了后续知识的掌握.所有的新知识,都要通过自身“再创造”,纳入到自己的认知结构中,成为有效而能发展的知识,优化和发展了数学认知结构.因此在教学过程中,要让学生经历“观察——猜想——归纳——验证”等一系列的数学活动,不断体会数形结合和从特殊到一般的数学思想方法.要给学生充足的研讨时间,化未知为已知,从而不断完善学生的认知体系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
