【精品原创】人教版数学九年级下册 29.3.1 《课题学习 制作立体模型》教案
文档属性
| 名称 | 【精品原创】人教版数学九年级下册 29.3.1 《课题学习 制作立体模型》教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册
29.3.1 课题学习 制作立体模型 教案
课题名 29.3.1 课题学习 制作立体模型
教学目标 1、体验平面图形向立体图形转化的过程.2、体会用三视图表示立体图形的作用。3、进一步感受平面图形与立体图形之间的关系
教学重点 会根据三视图制作立体模型.
教学难点 知识的综合运用
教学准备 教师准备:PPT、马铃薯.学生准备:硬纸板,马铃薯,橡皮泥.
教学过程
教学流程 教师活动 学生活动 设计意图
新课导入 科学家为了研究化学物质,制作出物质分子的立体模型 观看PPTf动画,进一步思考,科学家是如何制作这些研究模型的呢? 培养观察能力,并引入新课。
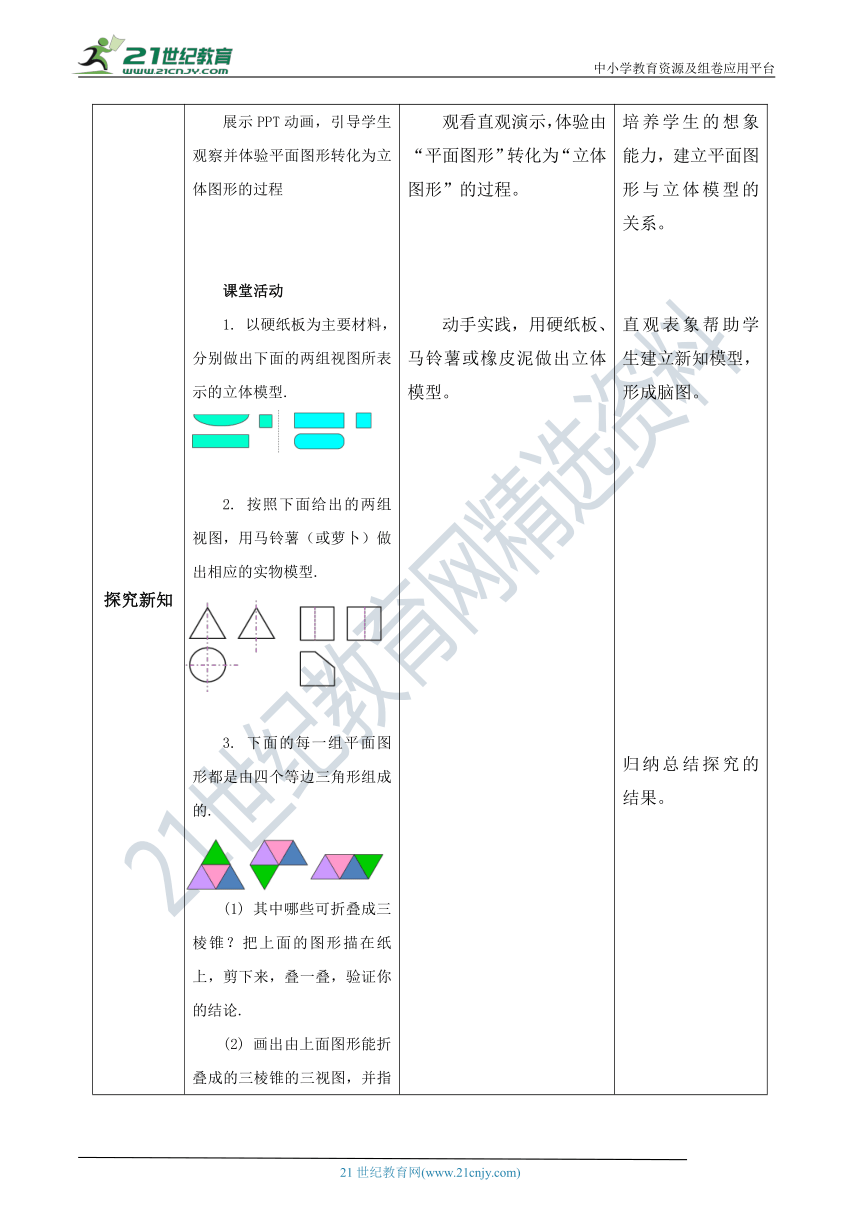
探究新知 展示PPT动画,引导学生观察并体验平面图形转化为立体图形的过程课堂活动1. 以硬纸板为主要材料,分别做出下面的两组视图所表示的立体模型.2. 按照下面给出的两组视图,用马铃薯(或萝卜)做出相应的实物模型.3. 下面的每一组平面图形都是由四个等边三角形组成的.(1) 其中哪些可折叠成三棱锥?把上面的图形描在纸上,剪下来,叠一叠,验证你的结论.(2) 画出由上面图形能折叠成的三棱锥的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的.(3) 如果上图中小三角形的边长为1,那么对应的三棱锥的表面积是多少?4. 下面的图形(如图)由一个扇形和一个圆组成.(1)把上面的图形描在纸上,剪下来,围成一个圆锥.(2)画出由上面图形围成的圆锥的三视图.(3)如果上图中扇形的半径为13,圆的半径为5,那么对应的圆锥的体积是多少? 观看直观演示,体验由“平面图形”转化为“立体图形”的过程。动手实践,用硬纸板、马铃薯或橡皮泥做出立体模型。求出一个边长为1的小三角形的面积,再求表面积。根据展开图得4个小三形,这样就容易得出立体图形的表面积。扇形的半径、圆的半径,可求出圆锥的高。 培养学生的想象能力,建立平面图形与立体模型的关系。直观表象帮助学生建立新知模型,形成脑图。归纳总结探究的结果。根据展开图或视图转化成立体模型,再求表面积或体积。培养学生的想象能力。
方法提炼 制作立体图形的一般步骤:通过视图想象物体的形状,将平面图形转化为立体图形,然后分组交流、合作、制作立体模型.注意:一般以硬纸板作为主要原料,或易切割的物体.
典例剖析 例1 一个几何体的展开图如图,把它折叠后能构成的立体图形是(A)A.三棱柱 B.三棱锥C.四棱柱 D.四棱锥
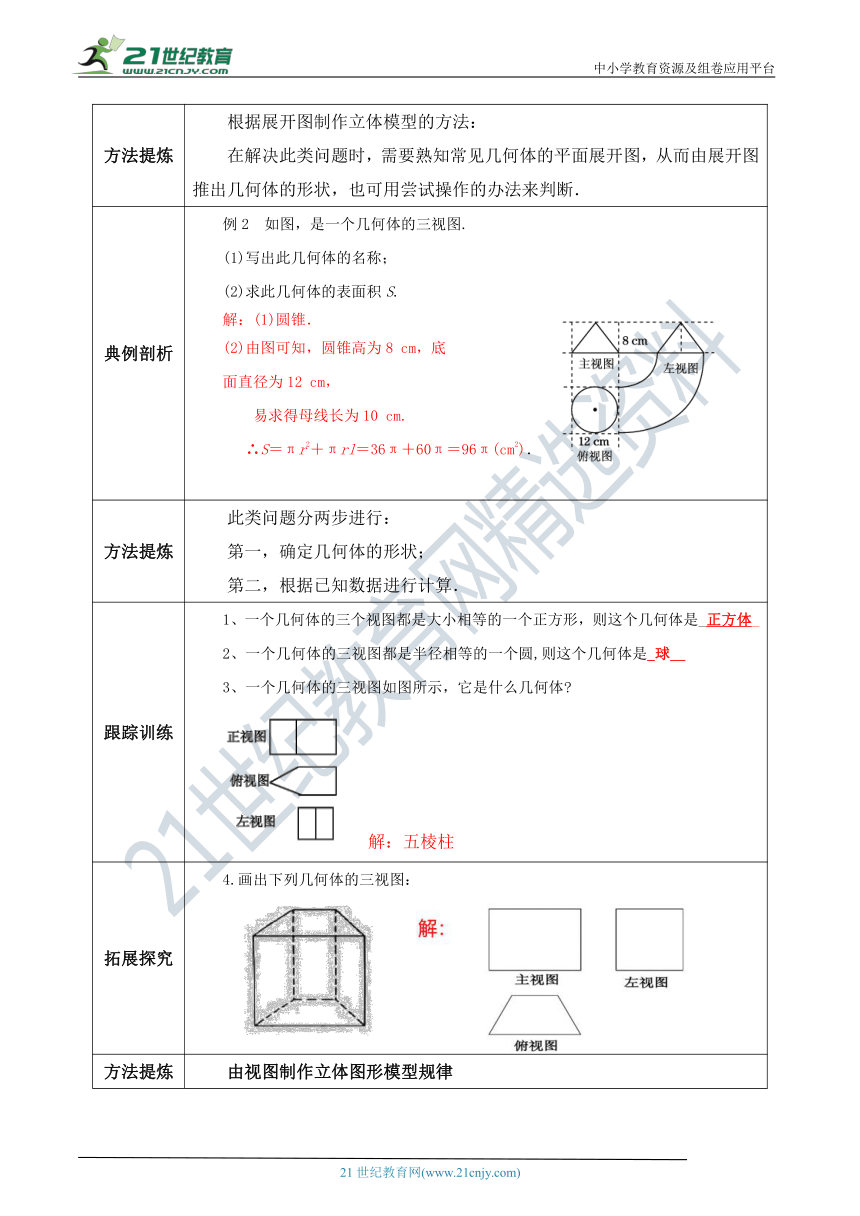
方法提炼 根据展开图制作立体模型的方法:在解决此类问题时,需要熟知常见几何体的平面展开图,从而由展开图推出几何体的形状,也可用尝试操作的办法来判断.
典例剖析 例2 如图,是一个几何体的三视图.(1)写出此几何体的名称;(2)求此几何体的表面积S.解:(1)圆锥.(2)由图可知,圆锥高为8 cm,底面直径为12 cm, 易求得母线长为10 cm. ∴S=πr2+πrl=36π+60π=96π(cm2).
方法提炼 此类问题分两步进行:第一,确定几何体的形状;第二,根据已知数据进行计算.
跟踪训练 1、一个几何体的三个视图都是大小相等的一个正方形,则这个几何体是_正方体_2、一个几何体的三视图都是半径相等的一个圆,则这个几何体是_球__3、一个几何体的三视图如图所示,它是什么几何体 ( http: / / www.21cnjy.com / )解:五棱柱
拓展探究 4.画出下列几何体的三视图: ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
方法提炼 由视图制作立体图形模型规律1、由三视图确定小立方体的个数,首先以俯视图为基准再由主视图和左视图从视线交叉角度去判断俯视图不同的位置上小立方体堆放的层数. 2、主视图、左视图、俯视图图形存在一定关系:主视图与左视图高平齐,主视图与俯视图长对正,俯视图与左视图宽相等.
链接中考 (中考·安徽省)几何体的三视图如图所示,这个几何体是( ) ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )【答案】C【解析】【分析】根据三视图,该几何体的主视图可确定该几何体的形状,据此求解即可.【详解】解:根据A,B,C,D三个选项的物体的主视图可知,与题图有吻合的只有C选项,故选:C.
随堂检测 1、三视图都一样的几何体有(球体、正方体) 2、如图是某几何体的三视图,则这个几何体是( 圆锥 ) ( http: / / www.21cnjy.com / )3、如图所示的三视图对应的几何体是( D ) ( http: / / www.21cnjy.com / )A圆柱 B圆锥 C长方体 D三棱柱4、下图是由大小相同的小正方体组成的几何体的主视图和左视图,那么组成这个几何体的小正方体的个数最多为( 7 ) ( http: / / www.21cnjy.com / )5、如图是一个上下底密封的纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积. (结果可保留根号) ( http: / / www.21cnjy.com / )解:2×6× × ××sin60°+6×12×5 =360+75 (cm )6、下图是一个几何体的俯视图,方框里的数据表示你能根据三视图该位置的小立方块的个数.请画出这个几何体的主视图、左视图. ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )7、如图,长方体长为4 cm,宽为2 cm, 高为5 cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,求蚂蚁爬行的最短路径长.解:作出这个长方体的侧面展开图,则最短路径如图为PQ. ( http: / / www.21cnjy.com / )∴
课堂小结 1.数学是以数量关系和空间形式 ( http: / / www.21cnjy.com )为主要研究对象 ( http: / / www.21cnjy.com )的科学,数量关系和空间形式是从现实世界中抽象出来的。例如,投影和视图的知识就是从建筑制造等中产生的,它们与实际模型联系得非常紧密2.感性认识需要上升为理性认识,理论指导下的实践会更明确有效3.从技能上说,认识平面图形与立体图形的联系,有助于根据需要实现它们之间的相互转化,即学会画三视图和由三视图得到立体图形.从能力上说,认识平面图形与立体图形的联系,对于培养空间想象能力是非常重要的。
教学反思 三视图和平面展开图是以不同方式描绘立体图形的 ( http: / / www.21cnjy.com ),本节课它们在生产实际中有直接应用.了解这方面的例子,可以丰富实践知识,进一步认识三视图和平面展开图.从技能上说,认识平面图形与立体图形的联系,有助于根据需要实现它们之间的相互转化,即学会画三视图和由三视图得出立体图形.从能力上说,认识平面图形与立体图形的联系,对于培养空间想象能力上非常重要的.同时,感性认识需要上升为理性认识,理论指导下的实践会更明确有效.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级下册
29.3.1 课题学习 制作立体模型 教案
课题名 29.3.1 课题学习 制作立体模型
教学目标 1、体验平面图形向立体图形转化的过程.2、体会用三视图表示立体图形的作用。3、进一步感受平面图形与立体图形之间的关系
教学重点 会根据三视图制作立体模型.
教学难点 知识的综合运用
教学准备 教师准备:PPT、马铃薯.学生准备:硬纸板,马铃薯,橡皮泥.
教学过程
教学流程 教师活动 学生活动 设计意图
新课导入 科学家为了研究化学物质,制作出物质分子的立体模型 观看PPTf动画,进一步思考,科学家是如何制作这些研究模型的呢? 培养观察能力,并引入新课。
探究新知 展示PPT动画,引导学生观察并体验平面图形转化为立体图形的过程课堂活动1. 以硬纸板为主要材料,分别做出下面的两组视图所表示的立体模型.2. 按照下面给出的两组视图,用马铃薯(或萝卜)做出相应的实物模型.3. 下面的每一组平面图形都是由四个等边三角形组成的.(1) 其中哪些可折叠成三棱锥?把上面的图形描在纸上,剪下来,叠一叠,验证你的结论.(2) 画出由上面图形能折叠成的三棱锥的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的.(3) 如果上图中小三角形的边长为1,那么对应的三棱锥的表面积是多少?4. 下面的图形(如图)由一个扇形和一个圆组成.(1)把上面的图形描在纸上,剪下来,围成一个圆锥.(2)画出由上面图形围成的圆锥的三视图.(3)如果上图中扇形的半径为13,圆的半径为5,那么对应的圆锥的体积是多少? 观看直观演示,体验由“平面图形”转化为“立体图形”的过程。动手实践,用硬纸板、马铃薯或橡皮泥做出立体模型。求出一个边长为1的小三角形的面积,再求表面积。根据展开图得4个小三形,这样就容易得出立体图形的表面积。扇形的半径、圆的半径,可求出圆锥的高。 培养学生的想象能力,建立平面图形与立体模型的关系。直观表象帮助学生建立新知模型,形成脑图。归纳总结探究的结果。根据展开图或视图转化成立体模型,再求表面积或体积。培养学生的想象能力。
方法提炼 制作立体图形的一般步骤:通过视图想象物体的形状,将平面图形转化为立体图形,然后分组交流、合作、制作立体模型.注意:一般以硬纸板作为主要原料,或易切割的物体.
典例剖析 例1 一个几何体的展开图如图,把它折叠后能构成的立体图形是(A)A.三棱柱 B.三棱锥C.四棱柱 D.四棱锥
方法提炼 根据展开图制作立体模型的方法:在解决此类问题时,需要熟知常见几何体的平面展开图,从而由展开图推出几何体的形状,也可用尝试操作的办法来判断.
典例剖析 例2 如图,是一个几何体的三视图.(1)写出此几何体的名称;(2)求此几何体的表面积S.解:(1)圆锥.(2)由图可知,圆锥高为8 cm,底面直径为12 cm, 易求得母线长为10 cm. ∴S=πr2+πrl=36π+60π=96π(cm2).
方法提炼 此类问题分两步进行:第一,确定几何体的形状;第二,根据已知数据进行计算.
跟踪训练 1、一个几何体的三个视图都是大小相等的一个正方形,则这个几何体是_正方体_2、一个几何体的三视图都是半径相等的一个圆,则这个几何体是_球__3、一个几何体的三视图如图所示,它是什么几何体 ( http: / / www.21cnjy.com / )解:五棱柱
拓展探究 4.画出下列几何体的三视图: ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
方法提炼 由视图制作立体图形模型规律1、由三视图确定小立方体的个数,首先以俯视图为基准再由主视图和左视图从视线交叉角度去判断俯视图不同的位置上小立方体堆放的层数. 2、主视图、左视图、俯视图图形存在一定关系:主视图与左视图高平齐,主视图与俯视图长对正,俯视图与左视图宽相等.
链接中考 (中考·安徽省)几何体的三视图如图所示,这个几何体是( ) ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )【答案】C【解析】【分析】根据三视图,该几何体的主视图可确定该几何体的形状,据此求解即可.【详解】解:根据A,B,C,D三个选项的物体的主视图可知,与题图有吻合的只有C选项,故选:C.
随堂检测 1、三视图都一样的几何体有(球体、正方体) 2、如图是某几何体的三视图,则这个几何体是( 圆锥 ) ( http: / / www.21cnjy.com / )3、如图所示的三视图对应的几何体是( D ) ( http: / / www.21cnjy.com / )A圆柱 B圆锥 C长方体 D三棱柱4、下图是由大小相同的小正方体组成的几何体的主视图和左视图,那么组成这个几何体的小正方体的个数最多为( 7 ) ( http: / / www.21cnjy.com / )5、如图是一个上下底密封的纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积. (结果可保留根号) ( http: / / www.21cnjy.com / )解:2×6× × ××sin60°+6×12×5 =360+75 (cm )6、下图是一个几何体的俯视图,方框里的数据表示你能根据三视图该位置的小立方块的个数.请画出这个几何体的主视图、左视图. ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )7、如图,长方体长为4 cm,宽为2 cm, 高为5 cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,求蚂蚁爬行的最短路径长.解:作出这个长方体的侧面展开图,则最短路径如图为PQ. ( http: / / www.21cnjy.com / )∴
课堂小结 1.数学是以数量关系和空间形式 ( http: / / www.21cnjy.com )为主要研究对象 ( http: / / www.21cnjy.com )的科学,数量关系和空间形式是从现实世界中抽象出来的。例如,投影和视图的知识就是从建筑制造等中产生的,它们与实际模型联系得非常紧密2.感性认识需要上升为理性认识,理论指导下的实践会更明确有效3.从技能上说,认识平面图形与立体图形的联系,有助于根据需要实现它们之间的相互转化,即学会画三视图和由三视图得到立体图形.从能力上说,认识平面图形与立体图形的联系,对于培养空间想象能力是非常重要的。
教学反思 三视图和平面展开图是以不同方式描绘立体图形的 ( http: / / www.21cnjy.com ),本节课它们在生产实际中有直接应用.了解这方面的例子,可以丰富实践知识,进一步认识三视图和平面展开图.从技能上说,认识平面图形与立体图形的联系,有助于根据需要实现它们之间的相互转化,即学会画三视图和由三视图得出立体图形.从能力上说,认识平面图形与立体图形的联系,对于培养空间想象能力上非常重要的.同时,感性认识需要上升为理性认识,理论指导下的实践会更明确有效.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
