【精品原创】人教版数学九年级下册 29.2.3 《由三视图确定几何体的面积或体积》教案
文档属性
| 名称 | 【精品原创】人教版数学九年级下册 29.2.3 《由三视图确定几何体的面积或体积》教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学七年级下册
29.2.3 由三视图确定几何体的面积或体积 教案
课题名 29.2.3 由三视图确定几何体的面积或体积
教学目标 1.能熟练地画出物体的三视图和由三视图想象出物体形状,进一步提高空间想象能力.2.由三视图想象出立体图形后能进行简单的面积或体积的计算.3.了解将三视图转化为立体图形在生产中的作用,体会三视图的实用价值.
教学重点 熟练地画出物体的三视图和由三视图想象出物体形状
教学难点 由三视图想象出立体图形后能进行简单的面积或体积的计算
教学准备 教师准备:PPT、刻度尺、量角器、三角板.学生准备:刻度尺、量角器、三角板.
教学过程
教学流程 教师活动 学生活动 设计意图
新课导入 如图,根据右边图中椅子的三视图,工人就能制造出符合设计要求的椅子. ( http: / / www.21cnjy.com / )你想知道他们是如何做到的吗?我们一起继续学习视图! 思考工人们是如何根据三视图如何制造椅子的呢? 培养观察能力,并引入新课。
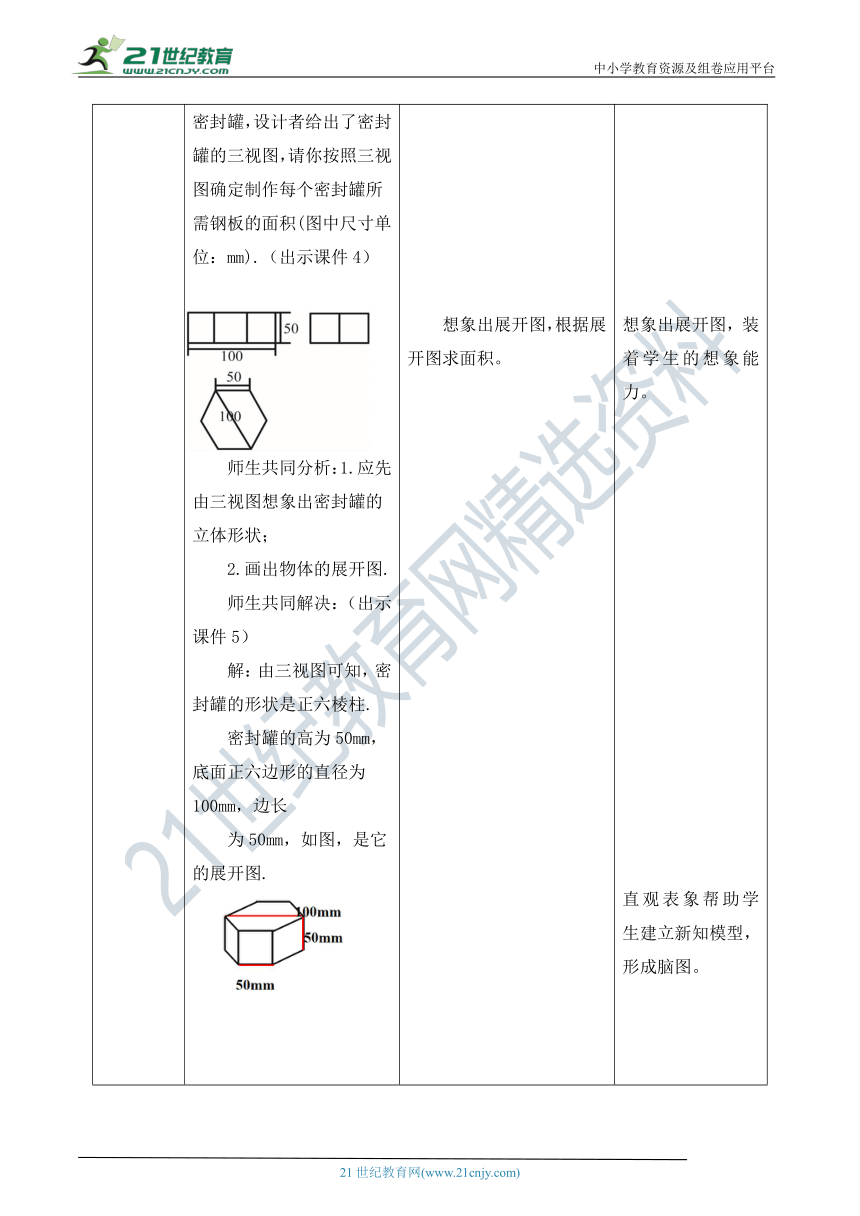
探究新知 知识点 三视图的有关计算考点1 利用三视图求物体的表面积.例 某工厂要加工一批密封罐,设计者给出了密封 ( http: / / www.21cnjy.com )罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm).(出示课件4)师生共同分析:1.应先由三视图想象出密封罐的立体形状;2.画出物体的展开图.师生共同解决:(出示课件5)解:由三视图可知,密封罐的形状是正六棱柱.密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,如图,是它的展开图. ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )由展开图可知,制作一个密封罐所需钢板的面积为 建立知识结构把“三视图”与“展开图”联系起来。想象出展开图,根据展开图求面积。解答,列式计算。 明确探究范围是 “三视图”。想象出展开图,装着学生的想象能力。直观表象帮助学生建立新知模型,形成脑图。培养学生数学学科素养,学会用数学语言表达证明步骤。归纳总结探究的结果。
方法提炼 由三视图求立体图形的面积的方法:(出示课件6)(1)先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.(2)将立体图形展开成一个平面图形(展开图),观察它的组成部分.(3)最后根据已知数据,求出展开图的面积.
跟踪训练 如图是一个几何体的三视图,试描绘出这个零件的形状,并求出此三视图所描述的几何体的表面积.解:该几何体是一个组合体,上部是一个圆锥,下部是一个圆柱,该几何体的表面积为π×22+2π×2×2+ ×4×4π=20 π. ( http: / / www.21cnjy.com / )
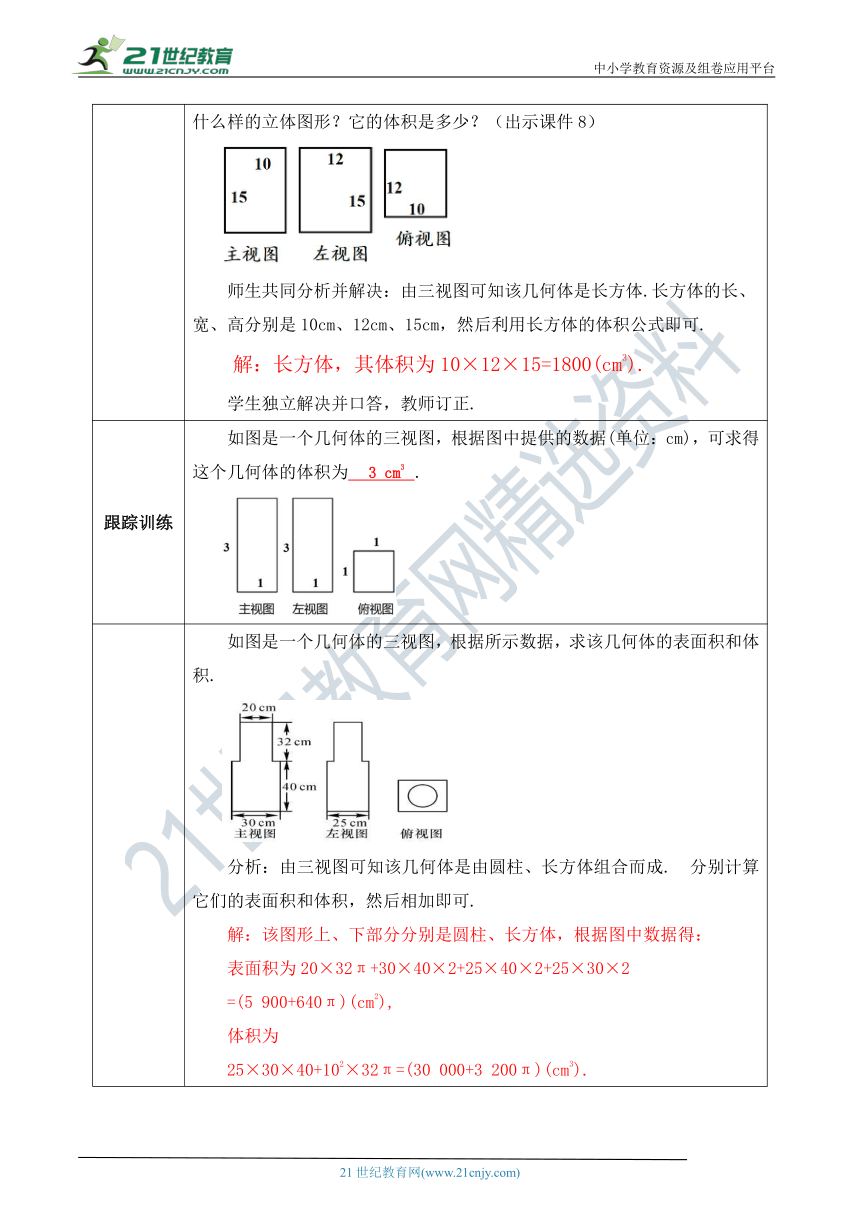
典例剖析 例 一个机器零件的三视图如图所示(单位:cm),这个机器零件是一个什么样的立体图形?它的体积是多少?(出示课件8) ( http: / / www.21cnjy.com / )师生共同分析并解决:由三视图可知该几何体是长方体.长方体的长、宽、高分别是10cm、12cm、15cm,然后利用长方体的体积公式即可.解:长方体,其体积为10×12×15=1800(cm3). 学生独立解决并口答,教师订正.
跟踪训练 如图是一个几何体的三视图,根据图中提供的数据(单位:cm),可求得这个几何体的体积为 3 cm3 . ( http: / / www.21cnjy.com / )
如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积. ( http: / / www.21cnjy.com / )分析:由三视图可知该几何体是由圆柱、长方体组合而成. 分别计算它们的表面积和体积,然后相加即可.解:该图形上、下部分分别是圆柱、长方体,根据图中数据得:表面积为20×32π+30×40×2+25×40×2+25×30×2=(5 900+640π)(cm2),体积为25×30×40+102×32π=(30 000+3 200π)(cm3).
拓展探究
链接中考 已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为 20π . ( http: / / www.21cnjy.com / )
随堂检测 1. 一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为 ( B ) ( http: / / www.21cnjy.com / )A. 6 B. 8 C. 12 D. 242.如图是一个几何体的三视图.根据图示,可计算出该几何体的侧面积为 104π . ( http: / / www.21cnjy.com / )3.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为2πcm2. ( http: / / www.21cnjy.com / )4.如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积. ( http: / / www.21cnjy.com / )分析:由三视图可知该几何体是由圆柱、长方体组合而成.分别计算它们的表面积和体积,然后相加即可.解:该图形上、下部分分别是圆柱、长方体,根据图中数据得: ( http: / / www.21cnjy.com / )表面积为20π×32+(30×40+25×40+25×30)×2=(5900+640π)(cm2),体积为25×30×40+102×32π=(30000+3200π)(cm3).5.如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图.(1)请写出构成这个几何体的正方体的个数为 5 ;(2)计算这个几何体的表面积为 20cm2 . ( http: / / www.21cnjy.com / )
课堂小结 1. 三种图形的转化:2. 由三视图求立体图形的体积 (或面积) 的方法:(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等;(2) 根据已知数据,求出立体图形的体积 (或将立体图形展开成一个平面图形,求出展开图的面积).
教学反思 本节课重在引导学生总结解决此类问题的方法和 ( http: / / www.21cnjy.com )规律,探究其实质.在小组讨论的过程中,学生了解了三视图中相关数据的对应关系,即“长对正,高平齐,宽相等”,找到了解决问题的根本,通过具体的例题,让学生进行练习,巩固学习效果.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学七年级下册
29.2.3 由三视图确定几何体的面积或体积 教案
课题名 29.2.3 由三视图确定几何体的面积或体积
教学目标 1.能熟练地画出物体的三视图和由三视图想象出物体形状,进一步提高空间想象能力.2.由三视图想象出立体图形后能进行简单的面积或体积的计算.3.了解将三视图转化为立体图形在生产中的作用,体会三视图的实用价值.
教学重点 熟练地画出物体的三视图和由三视图想象出物体形状
教学难点 由三视图想象出立体图形后能进行简单的面积或体积的计算
教学准备 教师准备:PPT、刻度尺、量角器、三角板.学生准备:刻度尺、量角器、三角板.
教学过程
教学流程 教师活动 学生活动 设计意图
新课导入 如图,根据右边图中椅子的三视图,工人就能制造出符合设计要求的椅子. ( http: / / www.21cnjy.com / )你想知道他们是如何做到的吗?我们一起继续学习视图! 思考工人们是如何根据三视图如何制造椅子的呢? 培养观察能力,并引入新课。
探究新知 知识点 三视图的有关计算考点1 利用三视图求物体的表面积.例 某工厂要加工一批密封罐,设计者给出了密封 ( http: / / www.21cnjy.com )罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm).(出示课件4)师生共同分析:1.应先由三视图想象出密封罐的立体形状;2.画出物体的展开图.师生共同解决:(出示课件5)解:由三视图可知,密封罐的形状是正六棱柱.密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,如图,是它的展开图. ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )由展开图可知,制作一个密封罐所需钢板的面积为 建立知识结构把“三视图”与“展开图”联系起来。想象出展开图,根据展开图求面积。解答,列式计算。 明确探究范围是 “三视图”。想象出展开图,装着学生的想象能力。直观表象帮助学生建立新知模型,形成脑图。培养学生数学学科素养,学会用数学语言表达证明步骤。归纳总结探究的结果。
方法提炼 由三视图求立体图形的面积的方法:(出示课件6)(1)先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.(2)将立体图形展开成一个平面图形(展开图),观察它的组成部分.(3)最后根据已知数据,求出展开图的面积.
跟踪训练 如图是一个几何体的三视图,试描绘出这个零件的形状,并求出此三视图所描述的几何体的表面积.解:该几何体是一个组合体,上部是一个圆锥,下部是一个圆柱,该几何体的表面积为π×22+2π×2×2+ ×4×4π=20 π. ( http: / / www.21cnjy.com / )
典例剖析 例 一个机器零件的三视图如图所示(单位:cm),这个机器零件是一个什么样的立体图形?它的体积是多少?(出示课件8) ( http: / / www.21cnjy.com / )师生共同分析并解决:由三视图可知该几何体是长方体.长方体的长、宽、高分别是10cm、12cm、15cm,然后利用长方体的体积公式即可.解:长方体,其体积为10×12×15=1800(cm3). 学生独立解决并口答,教师订正.
跟踪训练 如图是一个几何体的三视图,根据图中提供的数据(单位:cm),可求得这个几何体的体积为 3 cm3 . ( http: / / www.21cnjy.com / )
如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积. ( http: / / www.21cnjy.com / )分析:由三视图可知该几何体是由圆柱、长方体组合而成. 分别计算它们的表面积和体积,然后相加即可.解:该图形上、下部分分别是圆柱、长方体,根据图中数据得:表面积为20×32π+30×40×2+25×40×2+25×30×2=(5 900+640π)(cm2),体积为25×30×40+102×32π=(30 000+3 200π)(cm3).
拓展探究
链接中考 已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为 20π . ( http: / / www.21cnjy.com / )
随堂检测 1. 一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为 ( B ) ( http: / / www.21cnjy.com / )A. 6 B. 8 C. 12 D. 242.如图是一个几何体的三视图.根据图示,可计算出该几何体的侧面积为 104π . ( http: / / www.21cnjy.com / )3.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为2πcm2. ( http: / / www.21cnjy.com / )4.如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积. ( http: / / www.21cnjy.com / )分析:由三视图可知该几何体是由圆柱、长方体组合而成.分别计算它们的表面积和体积,然后相加即可.解:该图形上、下部分分别是圆柱、长方体,根据图中数据得: ( http: / / www.21cnjy.com / )表面积为20π×32+(30×40+25×40+25×30)×2=(5900+640π)(cm2),体积为25×30×40+102×32π=(30000+3200π)(cm3).5.如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图.(1)请写出构成这个几何体的正方体的个数为 5 ;(2)计算这个几何体的表面积为 20cm2 . ( http: / / www.21cnjy.com / )
课堂小结 1. 三种图形的转化:2. 由三视图求立体图形的体积 (或面积) 的方法:(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等;(2) 根据已知数据,求出立体图形的体积 (或将立体图形展开成一个平面图形,求出展开图的面积).
教学反思 本节课重在引导学生总结解决此类问题的方法和 ( http: / / www.21cnjy.com )规律,探究其实质.在小组讨论的过程中,学生了解了三视图中相关数据的对应关系,即“长对正,高平齐,宽相等”,找到了解决问题的根本,通过具体的例题,让学生进行练习,巩固学习效果.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
