【精品原创】人教版数学九年级下册 28.3.1 《锐角三角函数章末复习》教案
文档属性
| 名称 | 【精品原创】人教版数学九年级下册 28.3.1 《锐角三角函数章末复习》教案 |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:41 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学七年级下册
28.3.1 《锐角三角函数章末复习》 教案
课题名 28.3.1 《锐角三角函数章末复习》
教学目标 1.掌握3个考点内容.2.熟悉2个题型.3.突破1个易错点.
教学重点 熟练掌握3个考点的内容.
教学难点 熟悉2个题型及易错1个易错点.
教学准备 教师准备:PPT、刻度尺、量角器、三角板.学生准备:刻度尺、量角器、三角板.
教学过程
考点梳理 ( http: / / www.21cnjy.com / )答案: ( http: / / www.21cnjy.com / )特殊角的三角函数值 示意图α30°45°60°sinαcosαtanα1
考点专练 1.(2021·江西模拟)在Rt△ABC中,∠C=90°,AC=2,AB=6,则下列结论正确的是( )A.sinA= B.cosB=C.tanA=2 D.tanB=答案:C2.(2021·天津)tan 30°的值等于( )A. B. C.1 D.2答案:A
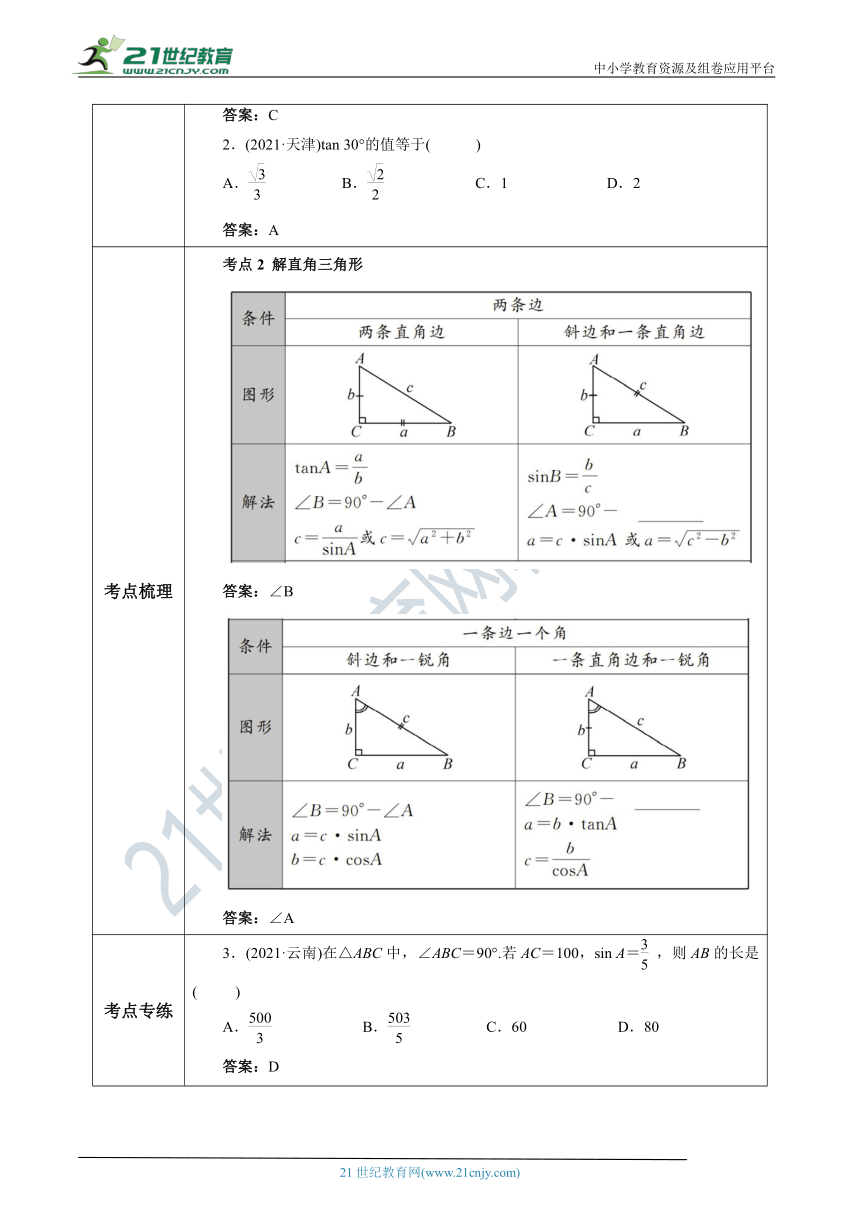
考点梳理 考点2 解直角三角形 ( http: / / www.21cnjy.com / )答案:∠B ( http: / / www.21cnjy.com / )答案:∠A
考点专练 3.(2021·云南)在△ABC中,∠ABC=90°.若AC=100,sin A=,则AB的长是( )A. B. C.60 D.80答案:D4.(2021·海南)如 ( http: / / www.21cnjy.com )图,△ABC的顶点B,C的坐标分别是(1,0),(0,),且∠ABC=90°,∠A=30°,则顶点A的坐标是____________. ( http: / / www.21cnjy.com / )答案:(4,)
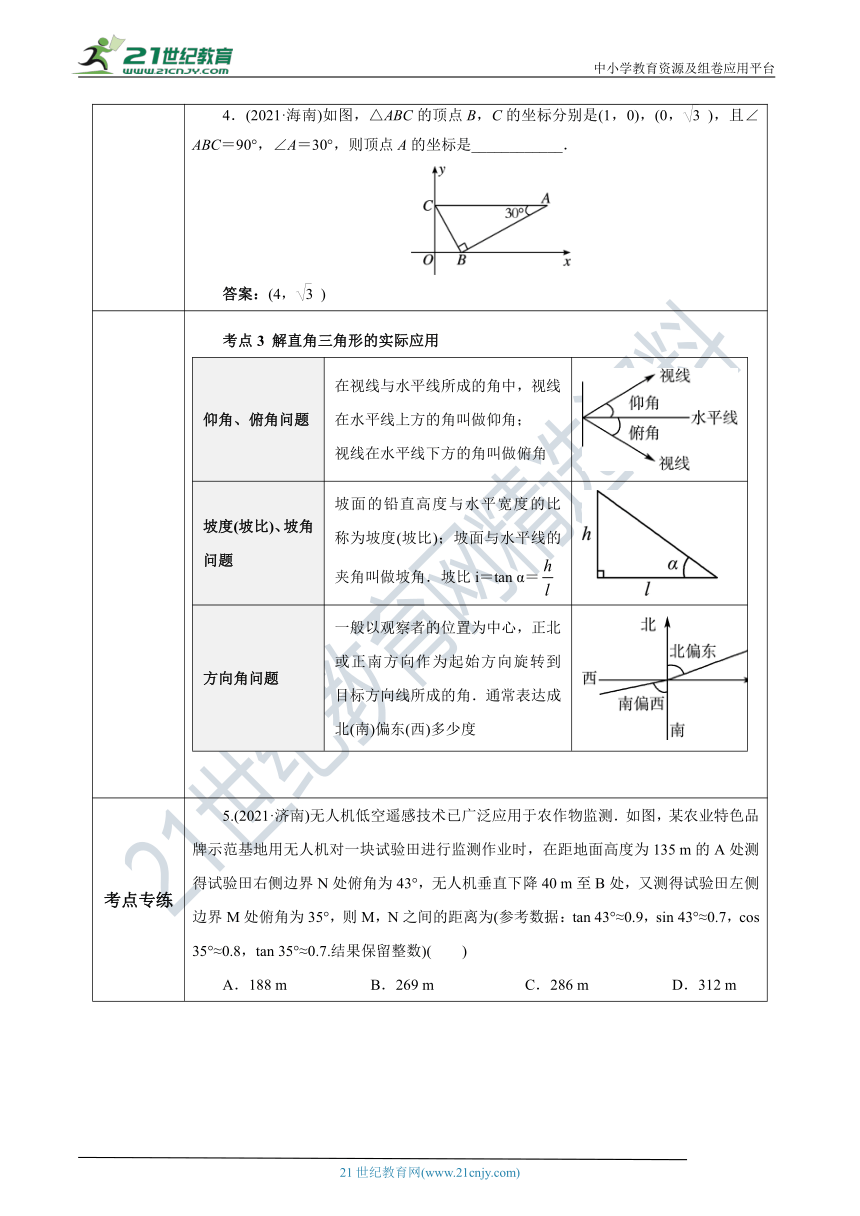
考点3 解直角三角形的实际应用仰角、俯角问题在视线与水平线所成的角中,视线在水平线上方的角叫做仰角;视线在水平线下方的角叫做俯角 ( http: / / www.21cnjy.com / )坡度(坡比)、坡角问题坡面的铅直高度与水平宽度的比称为坡度(坡比);坡面与水平线的夹角叫做坡角.坡比i=tan α= ( http: / / www.21cnjy.com / )方向角问题一般以观察者的位置为中心,正北或正南方向作为起始方向旋转到目标方向线所成的角.通常表达成北(南)偏东(西)多少度 ( http: / / www.21cnjy.com / )
考点专练 5.(2021·济南)无 ( http: / / www.21cnjy.com )人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为135 m的A处测得试验田右侧边界N处俯角为43°,无人机垂直下降40 m至B处,又测得试验田左侧边界M处俯角为35°,则M,N之间的距离为(参考数据:tan 43°≈0.9,sin 43°≈0.7,cos 35°≈0.8,tan 35°≈0.7.结果保留整数)( )A.188 m B.269 m C.286 m D.312 m ( http: / / www.21cnjy.com / )答案:C6.(2020·四川自贡)如图,我市在建高 ( http: / / www.21cnjy.com )铁的某段路基横断面为梯形ABCD,DC∥AB.BC长6米,坡角β为45°,AD的坡角α为30°,则AD长为________米(结果保留根号).答案:
母题剖析 题型一 与锐角三角函数相关的计算例1.(2021·巴中)如图,点A,B,C在边长为1的正方形网格格点上,下列结论错误的是( )A.sinB= B.sinC= C.tanB= D.sin2B+sin2C=1 ( http: / / www.21cnjy.com / )答案:A例2.(2021·贵港)如图,在矩形ABC ( http: / / www.21cnjy.com )D中,BD是对角线,AE⊥BD,垂足为E,连接CE,若tan∠ADB=,则tan ∠DEC的值是_________. ( http: / / www.21cnjy.com / )答案:
跟踪训练 1.(2021·宜昌)如图,△ABC的顶点是正方形网格的格点,则cos ∠ABC的值为( )A. B. C. D. ( http: / / www.21cnjy.com / )答案:B2.(2021·绍兴)如图,Rt ( http: / / www.21cnjy.com )△ABC中,∠BAC=90°,cos B=,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,连接CE,则的值为( )A. B. C. D.2 ( http: / / www.21cnjy.com / )答案:D
母题剖析 题型二 解直角三角形在实物情景中的应用例3.(2021·江西)图①是疫情期间测温 ( http: / / www.21cnjy.com )员用“额温枪”对小红测温时的实景图,图②是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28 cm,MB=42 cm,肘关节M与枪身端点A之间的水平宽度为25.3 cm(即MP的长度),枪身BA=8.5 cm.(1)求∠ABC的度数;(2)测温时规定枪身端点A与额头距离范围 ( http: / / www.21cnjy.com )为3~5 cm.在图②中,若测得∠BMN=68.6°,小红与测温员之间距离为50 cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)(参考数据:sin 66.4°≈0.92,cos 66.4°≈0.40,sin 23.6°≈0.40,≈1.414) ( http: / / www.21cnjy.com / )解:(1)如图②,过点B作BH⊥MP,垂足为H,过点M作MI⊥FG,垂足为I,过点P作PK⊥DE,垂足为K,∵MP=25.3 cm,BA=HP=8.5 cm,∴MH=MP-HP=25.3-8.5=16.8(cm),在Rt△BMH中,cos ∠BMH===0.4,∴∠BMH=66.4°,∵AB∥MP,∴∠BMH+∠ABC=180°,∴∠ABC=180°-66.4°=113.6°; ( http: / / www.21cnjy.com / )(2)∵∠BMN=68.6°,∠BMH=66.4°,∴∠NMI=180°-∠BMN-∠BMH=180°-68.6°-66.4°=45°,∵MN=28 cm,∴cos 45°==,∴MI≈19.80 cm,∵KI=50 cm,∴PK=KI-MI-MP=50-19.80-25.3=4.90≈5.0(cm),∴此时枪身端点A与小红额头的距离是在规定范围内.
跟踪训练 3.(2020·江西)如图①是一种手机 ( http: / / www.21cnjy.com )平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图.量得托板长AB=120 mm,支撑板长CD=80 mm,底座长DE=90 mm.托板AB固定在支撑板顶端点C处,且CB=40 mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(结果保留小数点后一位) ( http: / / www.21cnjy.com / )(1)若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离;(2)为了观看舒适,在(1)的情况下,把A ( http: / / www.21cnjy.com )B绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.(参考数据:sin 40°≈0 ( http: / / www.21cnjy.com ).643,cos 40°≈0.766,tan 40°≈0.839,sin 26.6°≈0.448,cos 26.6°≈0.894,tan 26.6°≈0.500,≈1.732)解:(1)过A作AM⊥DE,交ED的延长线于点M,过点C作CF⊥AM,垂足为F,过点C作CN⊥DE,垂足为N,由题意可知,AC=80,CD=80,∠DCB=80°,∠CDE=60°,在Rt△CDN中,CN=CD·sin ∠CDE=80×=40(mm)=FM,∠DCN=30°,又∵∠DCB=80°,∴∠BCN=50°,∵AM⊥DE,CN⊥DE,∴AM∥CN,∴∠A=∠BCN=50°,∴∠ACF=40°,在Rt△AFC中,AF=AC·sin 40°=80×0.643≈51.44,∴AM=AF+FM=51.44+40≈120.7(mm).答:点A到直线DE的距离约为120.7 mm; ( http: / / www.21cnjy.com / )(2)旋转后,如图③所示,根据题意可知∠DCB=80°+10°=90°,在Rt△BCD中,CD=80,BC=40,∴tan ∠D===0.500,∴∠D=26.6°,因此旋转的角度为:60°-26.6°=33.4°.答:CD旋转的角度约为33.4°.
随堂检测 1.(2021·江西模拟)锐角三角函数tan 45°的值为( )A. B. C. D.1答案:D2.(2021·金华)如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )A.4cosα米 B.4sinα米 C.4tanα米 D.米 ( http: / / www.21cnjy.com / )答案:A3.(2021·泰安)如图,为了 ( http: / / www.21cnjy.com )测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A,B,C,D,E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:≈1.732)( )A.136.6米 B.86.7米 C.186.7米 D.86.6米 ( http: / / www.21cnjy.com / )答案:A4.(2021·广元)如图,在4×4的正方形 ( http: / / www.21cnjy.com )网格图中,已知点A,B,C,D,O均在格点上,其中A,B,D又在⊙O上,点E是线段CD与⊙O的交点.则∠BAE的正切值为________. ( http: / / www.21cnjy.com / )答案:5.(2021·阜新)如图,甲楼高 ( http: / / www.21cnjy.com )21 m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为______m(结果精确到1 m,≈1.7). ( http: / / www.21cnjy.com / )答案:576.图①是一台实物投影仪,图②是它的示意图, ( http: / / www.21cnjy.com )折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8 cm,CD=8 cm,AB=30 cm,BC=35 cm.(结果精确到0.1). ( http: / / www.21cnjy.com / )(1)如图②,∠ABC=70°,BC∥OE.①填空:∠BAO=____°.②求投影探头的端点D到桌面OE的距离.(2)如图③,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6 cm时,求∠ABC的大小.(参考数据:sin 70°≈0.94,cos 20°≈0.94,sin 36.8°≈0.60,cos 53.2°≈0.60)解:(1)①过点A作AG∥BC,如图①,则∠BAG=∠ABC=70°,∵BC∥OE,∴AG∥OE,∴∠GAO=∠AOE=90°,∴∠BAO=90°+70°=160°;②过点A作AF⊥BC于点F,如图②,则AF=AB·sin ∠ABF=30sin 70°≈28.2(cm),∴投影探头的端点D到桌面OE的距离为:AF+OA-CD=28.2+6.8-8=27(cm); ( http: / / www.21cnjy.com / )(2)过点D作DH⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过A作AF⊥BM于点F,如图③,则∠MBA=70°,AF=28.2 cm,DH=6 cm,BC=35 cm,CD=8 cm,∴CM=AF+AO-DH-CD=28.2+6.8-6-8=21(cm),∴sin ∠MBC===0.6,∴∠MBC=36.8°,∴∠ABC=∠ABM-∠MBC=33.2°.
易错提示 中考失分点专练:没有先确定直角1.在直角三角形ABC中,若2AB=AC,则cos C=________________________.答案:或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学七年级下册
28.3.1 《锐角三角函数章末复习》 教案
课题名 28.3.1 《锐角三角函数章末复习》
教学目标 1.掌握3个考点内容.2.熟悉2个题型.3.突破1个易错点.
教学重点 熟练掌握3个考点的内容.
教学难点 熟悉2个题型及易错1个易错点.
教学准备 教师准备:PPT、刻度尺、量角器、三角板.学生准备:刻度尺、量角器、三角板.
教学过程
考点梳理 ( http: / / www.21cnjy.com / )答案: ( http: / / www.21cnjy.com / )特殊角的三角函数值 示意图α30°45°60°sinαcosαtanα1
考点专练 1.(2021·江西模拟)在Rt△ABC中,∠C=90°,AC=2,AB=6,则下列结论正确的是( )A.sinA= B.cosB=C.tanA=2 D.tanB=答案:C2.(2021·天津)tan 30°的值等于( )A. B. C.1 D.2答案:A
考点梳理 考点2 解直角三角形 ( http: / / www.21cnjy.com / )答案:∠B ( http: / / www.21cnjy.com / )答案:∠A
考点专练 3.(2021·云南)在△ABC中,∠ABC=90°.若AC=100,sin A=,则AB的长是( )A. B. C.60 D.80答案:D4.(2021·海南)如 ( http: / / www.21cnjy.com )图,△ABC的顶点B,C的坐标分别是(1,0),(0,),且∠ABC=90°,∠A=30°,则顶点A的坐标是____________. ( http: / / www.21cnjy.com / )答案:(4,)
考点3 解直角三角形的实际应用仰角、俯角问题在视线与水平线所成的角中,视线在水平线上方的角叫做仰角;视线在水平线下方的角叫做俯角 ( http: / / www.21cnjy.com / )坡度(坡比)、坡角问题坡面的铅直高度与水平宽度的比称为坡度(坡比);坡面与水平线的夹角叫做坡角.坡比i=tan α= ( http: / / www.21cnjy.com / )方向角问题一般以观察者的位置为中心,正北或正南方向作为起始方向旋转到目标方向线所成的角.通常表达成北(南)偏东(西)多少度 ( http: / / www.21cnjy.com / )
考点专练 5.(2021·济南)无 ( http: / / www.21cnjy.com )人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为135 m的A处测得试验田右侧边界N处俯角为43°,无人机垂直下降40 m至B处,又测得试验田左侧边界M处俯角为35°,则M,N之间的距离为(参考数据:tan 43°≈0.9,sin 43°≈0.7,cos 35°≈0.8,tan 35°≈0.7.结果保留整数)( )A.188 m B.269 m C.286 m D.312 m ( http: / / www.21cnjy.com / )答案:C6.(2020·四川自贡)如图,我市在建高 ( http: / / www.21cnjy.com )铁的某段路基横断面为梯形ABCD,DC∥AB.BC长6米,坡角β为45°,AD的坡角α为30°,则AD长为________米(结果保留根号).答案:
母题剖析 题型一 与锐角三角函数相关的计算例1.(2021·巴中)如图,点A,B,C在边长为1的正方形网格格点上,下列结论错误的是( )A.sinB= B.sinC= C.tanB= D.sin2B+sin2C=1 ( http: / / www.21cnjy.com / )答案:A例2.(2021·贵港)如图,在矩形ABC ( http: / / www.21cnjy.com )D中,BD是对角线,AE⊥BD,垂足为E,连接CE,若tan∠ADB=,则tan ∠DEC的值是_________. ( http: / / www.21cnjy.com / )答案:
跟踪训练 1.(2021·宜昌)如图,△ABC的顶点是正方形网格的格点,则cos ∠ABC的值为( )A. B. C. D. ( http: / / www.21cnjy.com / )答案:B2.(2021·绍兴)如图,Rt ( http: / / www.21cnjy.com )△ABC中,∠BAC=90°,cos B=,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,连接CE,则的值为( )A. B. C. D.2 ( http: / / www.21cnjy.com / )答案:D
母题剖析 题型二 解直角三角形在实物情景中的应用例3.(2021·江西)图①是疫情期间测温 ( http: / / www.21cnjy.com )员用“额温枪”对小红测温时的实景图,图②是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28 cm,MB=42 cm,肘关节M与枪身端点A之间的水平宽度为25.3 cm(即MP的长度),枪身BA=8.5 cm.(1)求∠ABC的度数;(2)测温时规定枪身端点A与额头距离范围 ( http: / / www.21cnjy.com )为3~5 cm.在图②中,若测得∠BMN=68.6°,小红与测温员之间距离为50 cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)(参考数据:sin 66.4°≈0.92,cos 66.4°≈0.40,sin 23.6°≈0.40,≈1.414) ( http: / / www.21cnjy.com / )解:(1)如图②,过点B作BH⊥MP,垂足为H,过点M作MI⊥FG,垂足为I,过点P作PK⊥DE,垂足为K,∵MP=25.3 cm,BA=HP=8.5 cm,∴MH=MP-HP=25.3-8.5=16.8(cm),在Rt△BMH中,cos ∠BMH===0.4,∴∠BMH=66.4°,∵AB∥MP,∴∠BMH+∠ABC=180°,∴∠ABC=180°-66.4°=113.6°; ( http: / / www.21cnjy.com / )(2)∵∠BMN=68.6°,∠BMH=66.4°,∴∠NMI=180°-∠BMN-∠BMH=180°-68.6°-66.4°=45°,∵MN=28 cm,∴cos 45°==,∴MI≈19.80 cm,∵KI=50 cm,∴PK=KI-MI-MP=50-19.80-25.3=4.90≈5.0(cm),∴此时枪身端点A与小红额头的距离是在规定范围内.
跟踪训练 3.(2020·江西)如图①是一种手机 ( http: / / www.21cnjy.com )平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图.量得托板长AB=120 mm,支撑板长CD=80 mm,底座长DE=90 mm.托板AB固定在支撑板顶端点C处,且CB=40 mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(结果保留小数点后一位) ( http: / / www.21cnjy.com / )(1)若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离;(2)为了观看舒适,在(1)的情况下,把A ( http: / / www.21cnjy.com )B绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.(参考数据:sin 40°≈0 ( http: / / www.21cnjy.com ).643,cos 40°≈0.766,tan 40°≈0.839,sin 26.6°≈0.448,cos 26.6°≈0.894,tan 26.6°≈0.500,≈1.732)解:(1)过A作AM⊥DE,交ED的延长线于点M,过点C作CF⊥AM,垂足为F,过点C作CN⊥DE,垂足为N,由题意可知,AC=80,CD=80,∠DCB=80°,∠CDE=60°,在Rt△CDN中,CN=CD·sin ∠CDE=80×=40(mm)=FM,∠DCN=30°,又∵∠DCB=80°,∴∠BCN=50°,∵AM⊥DE,CN⊥DE,∴AM∥CN,∴∠A=∠BCN=50°,∴∠ACF=40°,在Rt△AFC中,AF=AC·sin 40°=80×0.643≈51.44,∴AM=AF+FM=51.44+40≈120.7(mm).答:点A到直线DE的距离约为120.7 mm; ( http: / / www.21cnjy.com / )(2)旋转后,如图③所示,根据题意可知∠DCB=80°+10°=90°,在Rt△BCD中,CD=80,BC=40,∴tan ∠D===0.500,∴∠D=26.6°,因此旋转的角度为:60°-26.6°=33.4°.答:CD旋转的角度约为33.4°.
随堂检测 1.(2021·江西模拟)锐角三角函数tan 45°的值为( )A. B. C. D.1答案:D2.(2021·金华)如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )A.4cosα米 B.4sinα米 C.4tanα米 D.米 ( http: / / www.21cnjy.com / )答案:A3.(2021·泰安)如图,为了 ( http: / / www.21cnjy.com )测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A,B,C,D,E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:≈1.732)( )A.136.6米 B.86.7米 C.186.7米 D.86.6米 ( http: / / www.21cnjy.com / )答案:A4.(2021·广元)如图,在4×4的正方形 ( http: / / www.21cnjy.com )网格图中,已知点A,B,C,D,O均在格点上,其中A,B,D又在⊙O上,点E是线段CD与⊙O的交点.则∠BAE的正切值为________. ( http: / / www.21cnjy.com / )答案:5.(2021·阜新)如图,甲楼高 ( http: / / www.21cnjy.com )21 m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为______m(结果精确到1 m,≈1.7). ( http: / / www.21cnjy.com / )答案:576.图①是一台实物投影仪,图②是它的示意图, ( http: / / www.21cnjy.com )折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8 cm,CD=8 cm,AB=30 cm,BC=35 cm.(结果精确到0.1). ( http: / / www.21cnjy.com / )(1)如图②,∠ABC=70°,BC∥OE.①填空:∠BAO=____°.②求投影探头的端点D到桌面OE的距离.(2)如图③,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6 cm时,求∠ABC的大小.(参考数据:sin 70°≈0.94,cos 20°≈0.94,sin 36.8°≈0.60,cos 53.2°≈0.60)解:(1)①过点A作AG∥BC,如图①,则∠BAG=∠ABC=70°,∵BC∥OE,∴AG∥OE,∴∠GAO=∠AOE=90°,∴∠BAO=90°+70°=160°;②过点A作AF⊥BC于点F,如图②,则AF=AB·sin ∠ABF=30sin 70°≈28.2(cm),∴投影探头的端点D到桌面OE的距离为:AF+OA-CD=28.2+6.8-8=27(cm); ( http: / / www.21cnjy.com / )(2)过点D作DH⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过A作AF⊥BM于点F,如图③,则∠MBA=70°,AF=28.2 cm,DH=6 cm,BC=35 cm,CD=8 cm,∴CM=AF+AO-DH-CD=28.2+6.8-6-8=21(cm),∴sin ∠MBC===0.6,∴∠MBC=36.8°,∴∠ABC=∠ABM-∠MBC=33.2°.
易错提示 中考失分点专练:没有先确定直角1.在直角三角形ABC中,若2AB=AC,则cos C=________________________.答案:或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
