【精品原创】人教版数学九年级下册 27.2.1.2 《相似三角形的判定2》教案
文档属性
| 名称 | 【精品原创】人教版数学九年级下册 27.2.1.2 《相似三角形的判定2》教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版数学七年级下册
27.2.1.2 相似三角形的判定2 教案
课题名 27.2.1.2 相似三角形的判定2
教学目标 1、掌握“三边对应成比例,两个三角形相似”的判定方法.并初步应用。2、通过类比观察、猜想、证明等活动,探索相似三角形判定定理证明的过程体会转化的数学思想。3、进一步积累研究几何图形问题的经验。
教学重点 三边对应相等,两三角形相似的相似三角形判定定理的证明及初步应用
教学难点 相似三角形判定定理证明过程中在比例式中得到线段相等的关系
教学准备 教师准备:PPT学生准备:坐标纸、错题本、习题本、课堂笔记
教学过程
教学流程 教师活动 学生活动 设计意图
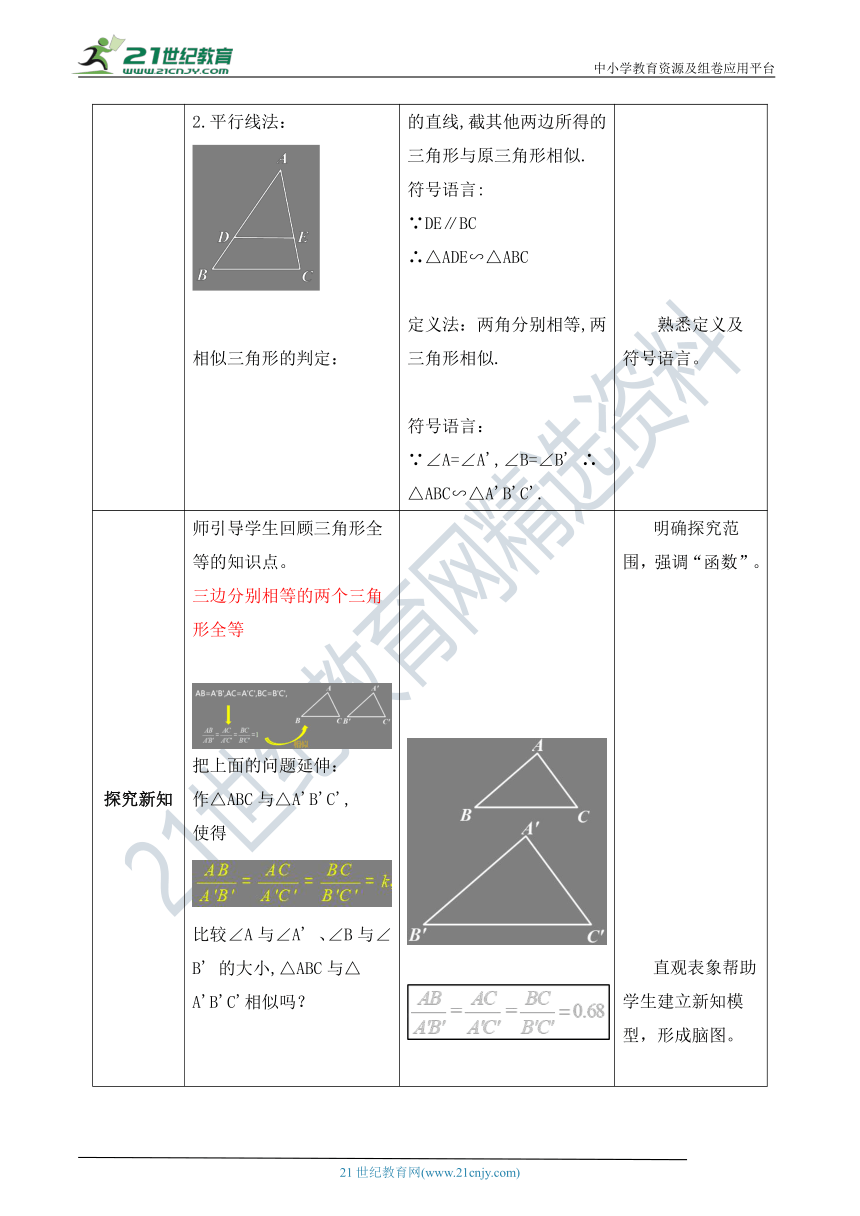
新课导入 请同学们回忆相似三角形的定义。1、定义法:几何语言:2.平行线法:相似三角形的判定: 对应角相等,对应边成比例的两个三角形叫做相似三角形.∵∠A=∠A',∠B=∠B',∠C=∠C' ( http: / / www.21cnjy.com / )∴ △ABC∽△A'B'C' .定义法:平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.符号语言:∵DE∥BC∴△ADE∽△ABC定义法:两角分别相等,两三角形相似.符号语言:∵∠A=∠A',∠B=∠B' ∴△ABC∽△A'B'C'. 培养观察能力,并引入新课。熟悉定义及符号语言。
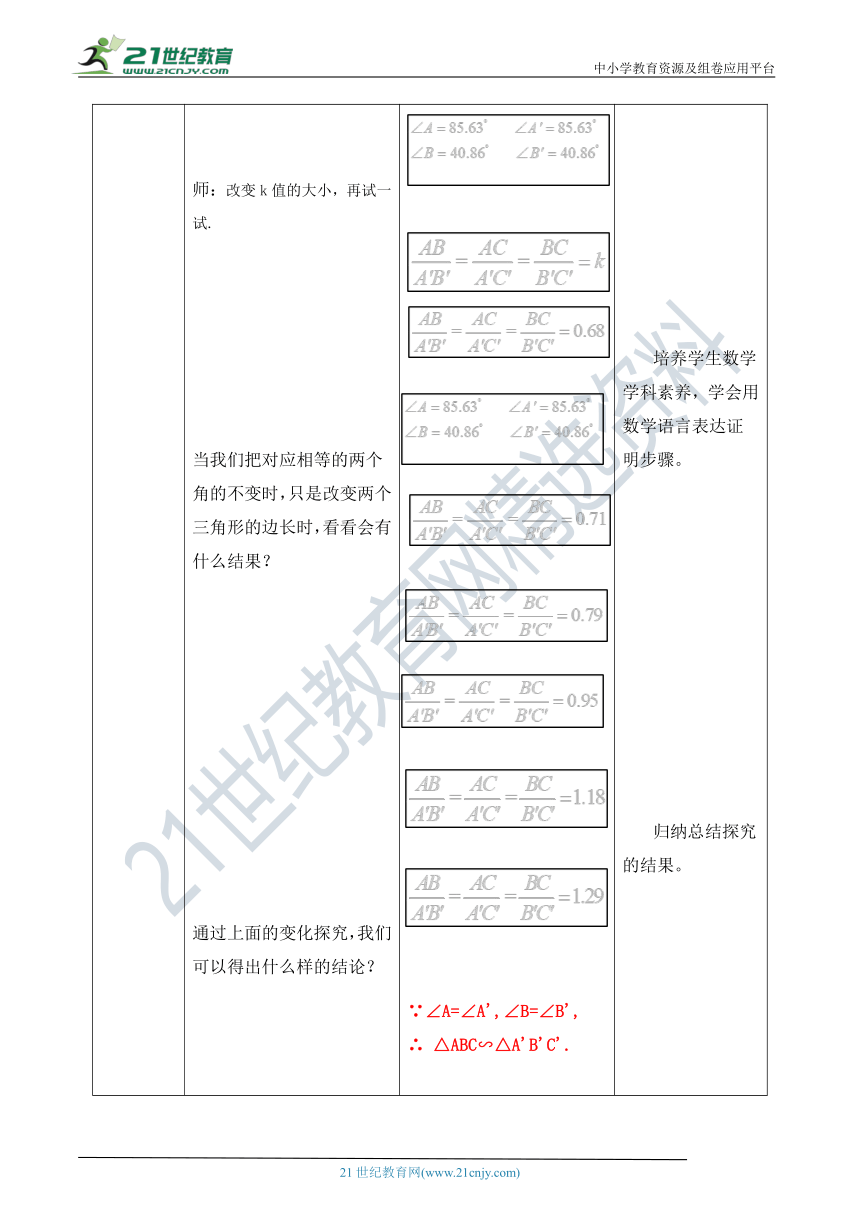
探究新知 师引导学生回顾三角形全等的知识点。三边分别相等的两个三角形全等把上面的问题延伸:作△ABC与△A'B'C',使得比较∠A与∠A' 、∠B与∠B' 的大小,△ABC与△A'B'C'相似吗?师:改变k值的大小,再试一试.当我们把对应相等的两个角的不变时,只是改变两个三角形的边长时,看看会有什么结果?通过上面的变化探究,我们可以得出什么样的结论? ∵∠A=∠A',∠B=∠B', ∴ △ABC∽△A'B'C'. 明确探究范围,强调“函数”。直观表象帮助学生建立新知模型,形成脑图。培养学生数学学科素养,学会用数学语言表达证明步骤。归纳总结探究的结果。
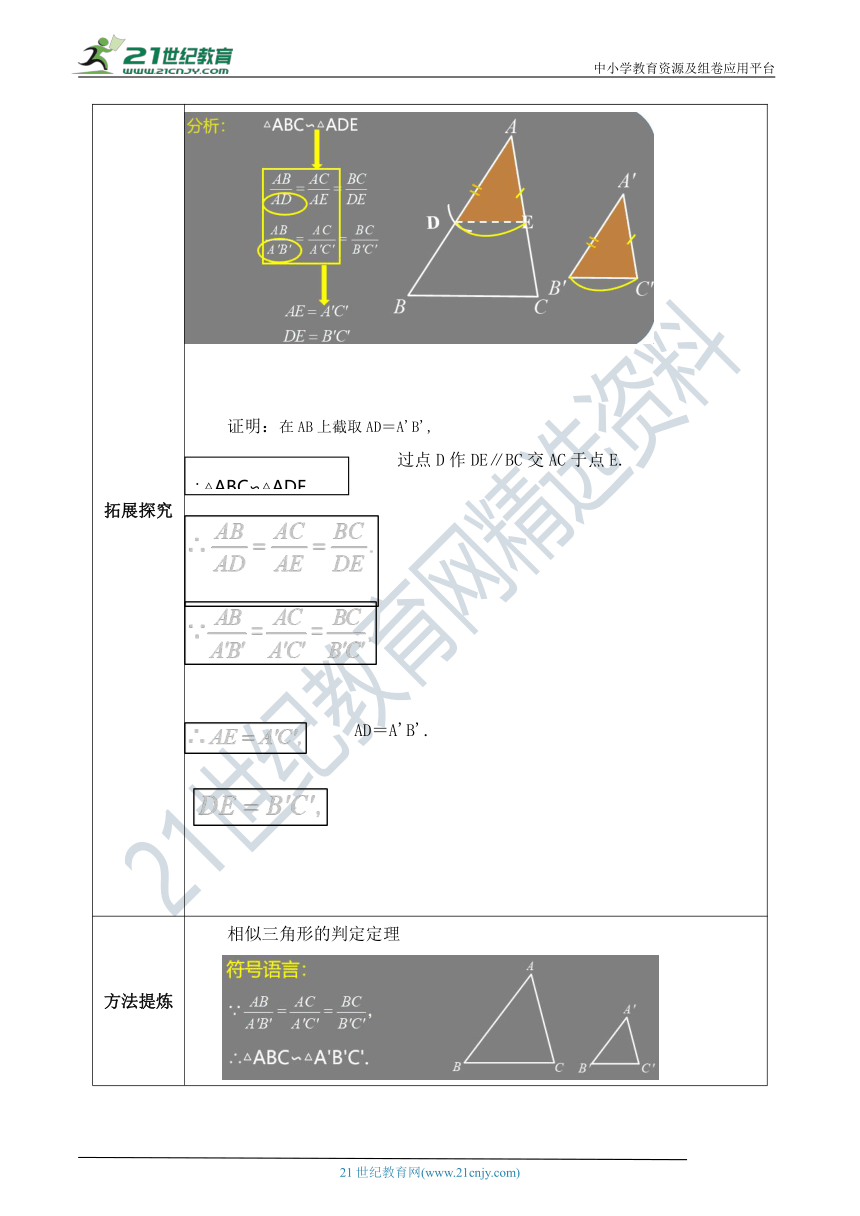
拓展探究 证明:在AB上截取AD=A'B',过点D作DE∥BC交AC于点E.AD=A'B'.
方法提炼 相似三角形的判定定理 ( http: / / www.21cnjy.com / )
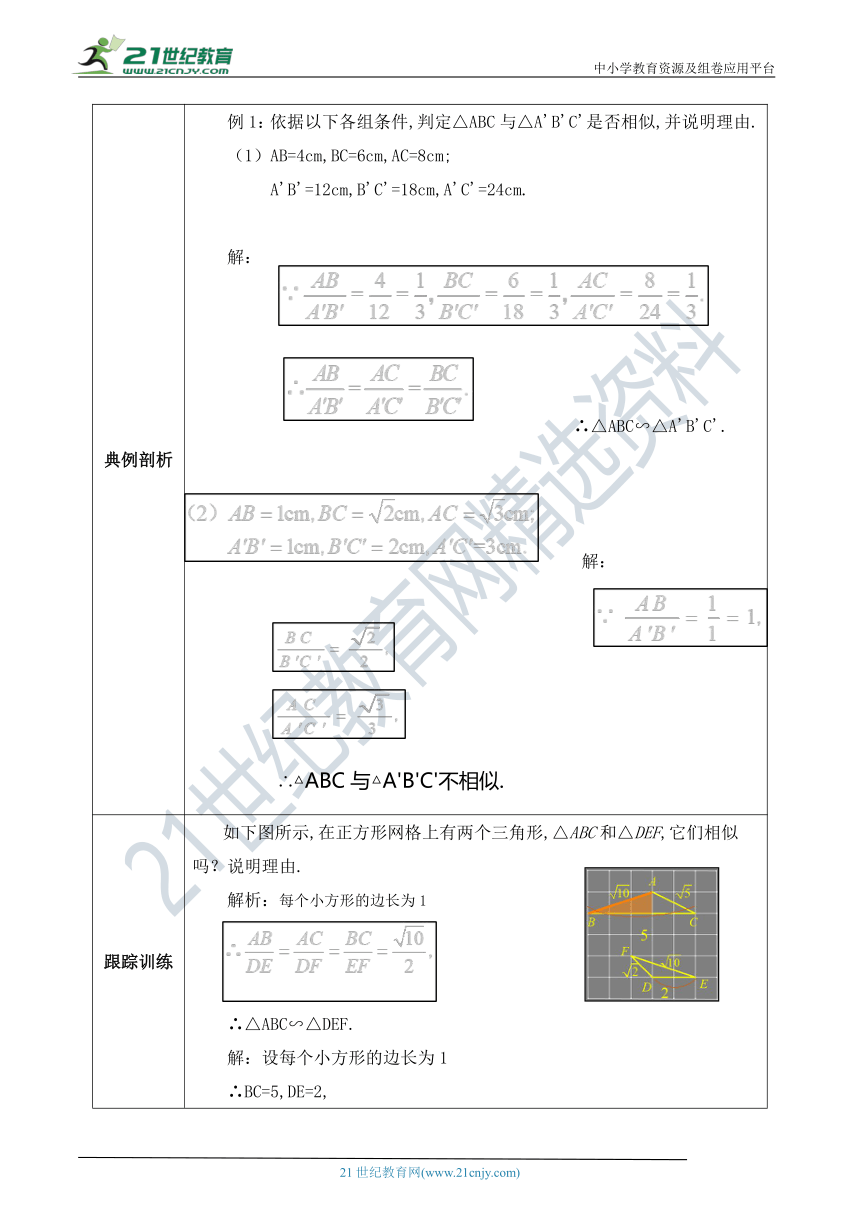
典例剖析 例1:依据以下各组条件,判定△ABC与△A'B'C'是否相似,并说明理由.(1)AB=4cm,BC=6cm,AC=8cm; A'B'=12cm,B'C'=18cm,A'C'=24cm.解:∴△ABC∽△A'B'C'.解:
跟踪训练 如下图所示,在正方形网格上有两个三角形,△ABC和△DEF,它们相似吗?说明理由.解析:每个小方形的边长为1 ( http: / / www.21cnjy.com / )∴△ABC∽△DEF.解:设每个小方形的边长为1∴BC=5,DE=2,由勾股定理可得 同理可得 ( http: / / www.21cnjy.com / )∴△ABC∽△DEF.
链接中考 如图,小正方形的边长均为1,则下列图中的三 角形(阴影部分)与△ABC相似的是( B )A. B. C. D.
随堂检测 1.要做两个形状相同的三角形框架, ( http: / / www.21cnjy.com )其中一个三角形框架的三边长分别为4cm,5cm,6cm,另一个三角形框架的一边长为2cm,怎样选料可使这两个三角形相似? 【解析】解:要使这两个三角形相似,则这两个三角形的三边对应成比例.有三种情况:(1)如果边长为4,5,6的对应边长分别为2,x,y, 那么: 解得:x=2.5 y=3(2)如果边长为4,5,6的对应边长分别为x,2,y, 那么: 解得:x=1.6 y=2.4(3)如果边长为4,5,6的对应边长分别为x,y,2, 那么: 解得:2.已知:点D,E,F分别是△ABC三边的中点.求证:△EFD∽△ABC.证明:∵点D,E,F分别是△ABC三边的中点.∴△EFD∽△ABC.
课堂小结 1.知识:(1)定义:三个角分别相等,三条边对应成比例的两个三角形相似.(2)平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.(3)判定定理:两角分别相等,两三角形相似.(4)判定定理:三边对应成比例,两三角形相似.2.方法:(1)通过类比学习,把未知问题转化为已知问题,体现了转化和类比思想,这两种思想方法也是学习数学过程中常用的思想方法.2)本节课的课堂练习,体现了分类讨论的学习方法,这种方法能够使我们解决问题时考虑的更加全面.
教学反思 因为本课时教学过程中主要是让 ( http: / / www.21cnjy.com )学生采用类比的方法先猜想出命题,然后证明猜想的命题是否正确.课堂上教师主要还是以提问的形式,逐步引导学生去证明命题.在本节课中要放手给学生动脑、动手的机会,要注意面向全体学生.
∴△ABC∽△ADE,
∴△ABC与△A'B'C'不相似.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学七年级下册
27.2.1.2 相似三角形的判定2 教案
课题名 27.2.1.2 相似三角形的判定2
教学目标 1、掌握“三边对应成比例,两个三角形相似”的判定方法.并初步应用。2、通过类比观察、猜想、证明等活动,探索相似三角形判定定理证明的过程体会转化的数学思想。3、进一步积累研究几何图形问题的经验。
教学重点 三边对应相等,两三角形相似的相似三角形判定定理的证明及初步应用
教学难点 相似三角形判定定理证明过程中在比例式中得到线段相等的关系
教学准备 教师准备:PPT学生准备:坐标纸、错题本、习题本、课堂笔记
教学过程
教学流程 教师活动 学生活动 设计意图
新课导入 请同学们回忆相似三角形的定义。1、定义法:几何语言:2.平行线法:相似三角形的判定: 对应角相等,对应边成比例的两个三角形叫做相似三角形.∵∠A=∠A',∠B=∠B',∠C=∠C' ( http: / / www.21cnjy.com / )∴ △ABC∽△A'B'C' .定义法:平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.符号语言:∵DE∥BC∴△ADE∽△ABC定义法:两角分别相等,两三角形相似.符号语言:∵∠A=∠A',∠B=∠B' ∴△ABC∽△A'B'C'. 培养观察能力,并引入新课。熟悉定义及符号语言。
探究新知 师引导学生回顾三角形全等的知识点。三边分别相等的两个三角形全等把上面的问题延伸:作△ABC与△A'B'C',使得比较∠A与∠A' 、∠B与∠B' 的大小,△ABC与△A'B'C'相似吗?师:改变k值的大小,再试一试.当我们把对应相等的两个角的不变时,只是改变两个三角形的边长时,看看会有什么结果?通过上面的变化探究,我们可以得出什么样的结论? ∵∠A=∠A',∠B=∠B', ∴ △ABC∽△A'B'C'. 明确探究范围,强调“函数”。直观表象帮助学生建立新知模型,形成脑图。培养学生数学学科素养,学会用数学语言表达证明步骤。归纳总结探究的结果。
拓展探究 证明:在AB上截取AD=A'B',过点D作DE∥BC交AC于点E.AD=A'B'.
方法提炼 相似三角形的判定定理 ( http: / / www.21cnjy.com / )
典例剖析 例1:依据以下各组条件,判定△ABC与△A'B'C'是否相似,并说明理由.(1)AB=4cm,BC=6cm,AC=8cm; A'B'=12cm,B'C'=18cm,A'C'=24cm.解:∴△ABC∽△A'B'C'.解:
跟踪训练 如下图所示,在正方形网格上有两个三角形,△ABC和△DEF,它们相似吗?说明理由.解析:每个小方形的边长为1 ( http: / / www.21cnjy.com / )∴△ABC∽△DEF.解:设每个小方形的边长为1∴BC=5,DE=2,由勾股定理可得 同理可得 ( http: / / www.21cnjy.com / )∴△ABC∽△DEF.
链接中考 如图,小正方形的边长均为1,则下列图中的三 角形(阴影部分)与△ABC相似的是( B )A. B. C. D.
随堂检测 1.要做两个形状相同的三角形框架, ( http: / / www.21cnjy.com )其中一个三角形框架的三边长分别为4cm,5cm,6cm,另一个三角形框架的一边长为2cm,怎样选料可使这两个三角形相似? 【解析】解:要使这两个三角形相似,则这两个三角形的三边对应成比例.有三种情况:(1)如果边长为4,5,6的对应边长分别为2,x,y, 那么: 解得:x=2.5 y=3(2)如果边长为4,5,6的对应边长分别为x,2,y, 那么: 解得:x=1.6 y=2.4(3)如果边长为4,5,6的对应边长分别为x,y,2, 那么: 解得:2.已知:点D,E,F分别是△ABC三边的中点.求证:△EFD∽△ABC.证明:∵点D,E,F分别是△ABC三边的中点.∴△EFD∽△ABC.
课堂小结 1.知识:(1)定义:三个角分别相等,三条边对应成比例的两个三角形相似.(2)平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.(3)判定定理:两角分别相等,两三角形相似.(4)判定定理:三边对应成比例,两三角形相似.2.方法:(1)通过类比学习,把未知问题转化为已知问题,体现了转化和类比思想,这两种思想方法也是学习数学过程中常用的思想方法.2)本节课的课堂练习,体现了分类讨论的学习方法,这种方法能够使我们解决问题时考虑的更加全面.
教学反思 因为本课时教学过程中主要是让 ( http: / / www.21cnjy.com )学生采用类比的方法先猜想出命题,然后证明猜想的命题是否正确.课堂上教师主要还是以提问的形式,逐步引导学生去证明命题.在本节课中要放手给学生动脑、动手的机会,要注意面向全体学生.
∴△ABC∽△ADE,
∴△ABC与△A'B'C'不相似.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
