【精品原创】人教版数学九年级下册 27.3.2 《位似2》练习(含解析)
文档属性
| 名称 | 【精品原创】人教版数学九年级下册 27.3.2 《位似2》练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:41 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册
27.3.2 位似2 课后练习
一.选择题(共7小题)
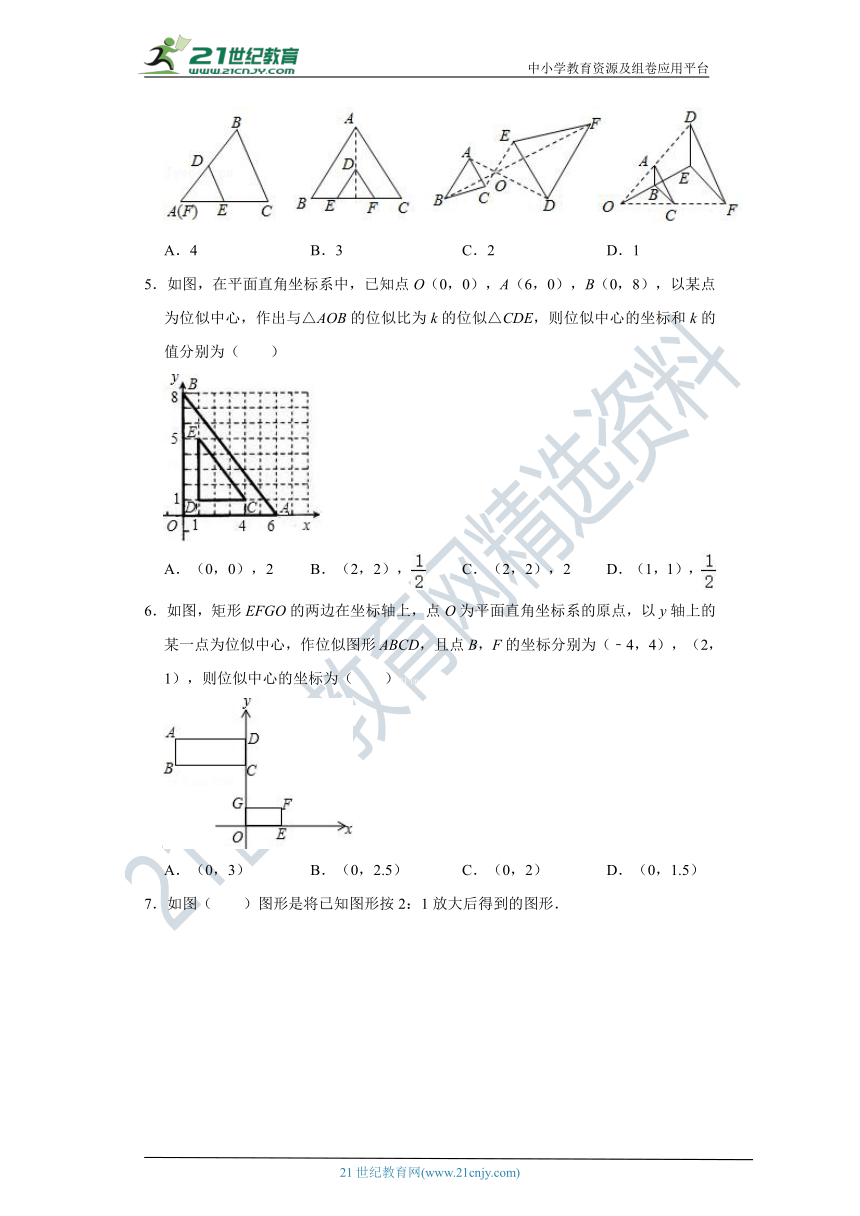
1.如图,在坐标系中,以A(0, ( http: / / www.21cnjy.com )2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )
( http: / / www.21cnjy.com / )
A.(m,n+3) B.(m,n﹣3)
C.(m,n+2) D.(m,n﹣2)
2.如图所示是△ABC位似图形的几种画法,其中正确的是个数是( )
( http: / / www.21cnjy.com / )
A.1 B.2 C.3 D.4
3.用位似方法把图形扩大或缩小时,下列说法中,正确的是( )
A.位似中心要么取在图形外部,要么取在图形内部
B.位似中心取在图形内部时,只能把图形缩小
C.当位似中心确定后,按要求放大或缩小的图形只能画一个
D.以上说法都不正确
4.如图所示△DEF是△ABC位似图形的几种画法,其中正确的个数是( )
( http: / / www.21cnjy.com / )
A.4 B.3 C.2 D.1
5.如图,在平面直角坐标系中,已知点O(0, ( http: / / www.21cnjy.com )0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )21教育网
( http: / / www.21cnjy.com / )
A.(0,0),2 B.(2,2), C.(2,2),2 D.(1,1),
6.如图,矩形EFGO的两边在 ( http: / / www.21cnjy.com )坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标为( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.(0,3) B.(0,2.5) C.(0,2) D.(0,1.5)
7.如图( )图形是将已知图形按2:1放大后得到的图形.
( http: / / www.21cnjy.com / )
A.A B.B C.C D.D
二.填空题(共5小题)
8.已知△ABC在坐标平 ( http: / / www.21cnjy.com )面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以B为位似中心,画出△A1B1C1与△ABC相似,两三角形位于点B同侧且相似比是3,则点C的对应顶点C1的坐标是 .21·世纪*教育网
9.如图,△A′B′C′与△ABC关于y轴对称,已知A(1,4),B(3,1),C(3,3),若以原点O为位似中心,相似比为作△A′B′C′的缩小的位似图形△A″B″C″,则A″的坐标是 .21*cnjy*com
( http: / / www.21cnjy.com / )
10.如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA=2.OC=1,则矩形AOCB的对称中心的坐标是 ;在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2,…,按此规律,则矩形A4OC4B4的对称中心的坐标是 .21世纪教育网版权所有
( http: / / www.21cnjy.com / )
11.已知:如图△ABC ( http: / / www.21cnjy.com )三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画出△A1B1C1,使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,此时点A1的坐标为 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
12.在平面直角坐标系中,△ABC顶点A的坐 ( http: / / www.21cnjy.com )标为(2,3),若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比等于2:1,则点A′的坐标 .【出处:21教育名师】
三.解答题(共3小题)
13.如图,在由边长为1个单位的长度的小正方形组成的网格图中,已知点O及△ABC的顶点均为网格线的交点.21教育名师原创作品
(1)在给定网格中,以O为位似中心,将△ABC放大为原来的三倍,得到请△A'B'C',请画出△A'B'C';21*cnjy*com
(2)B'C'的长度为 单位长度,△A′B′C′的面积为 平方单位.
( http: / / www.21cnjy.com / )
14.放缩尺是一种绘图工具,它能把图形放大或缩小.
制作:把钻有若干等距小孔的四 ( http: / / www.21cnjy.com )根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点,OD=DA=CB,DC=AB=BE,在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
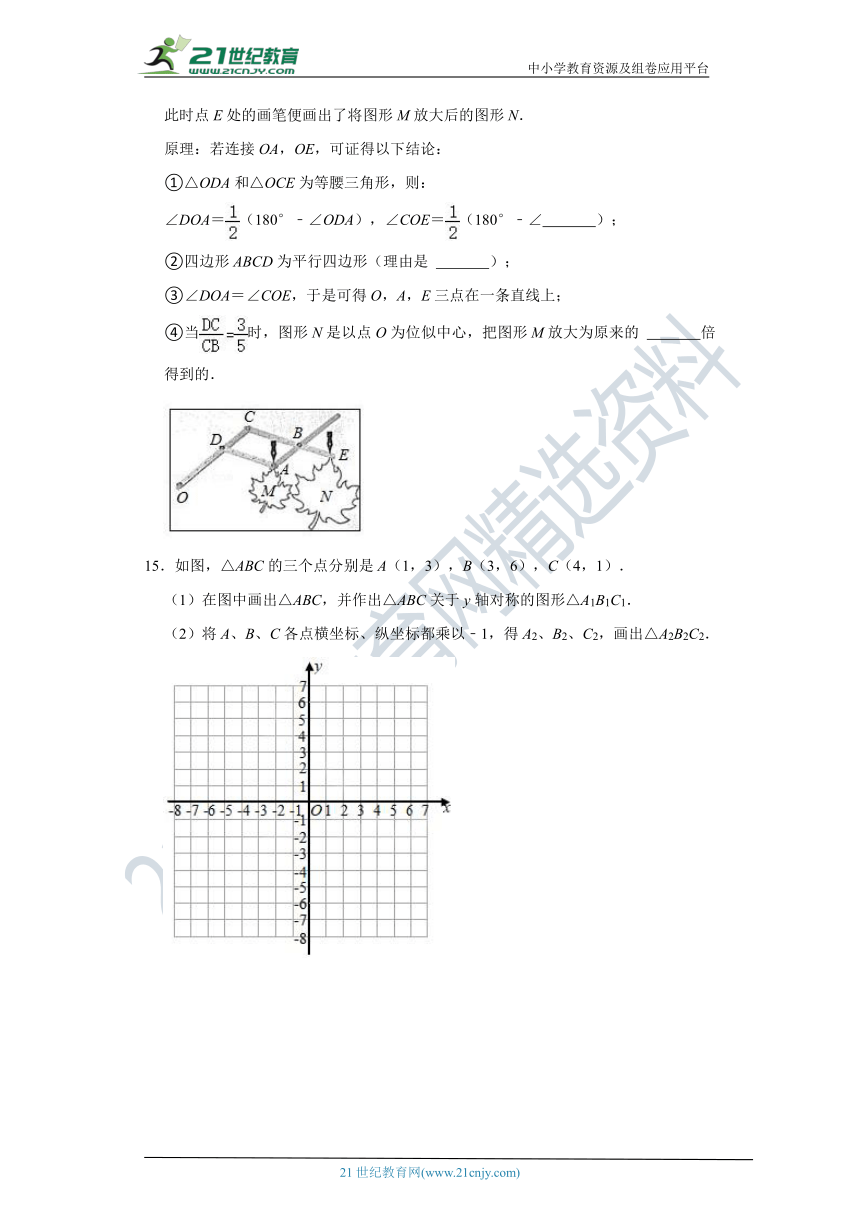
原理:若连接OA,OE,可证得以下结论:
①△ODA和△OCE为等腰三角形,则:
∠DOA=(180°﹣∠ODA),∠COE=(180°﹣∠ );
②四边形ABCD为平行四边形(理由是 );
③∠DOA=∠COE,于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 倍得到的.
( http: / / www.21cnjy.com / )
15.如图,△ABC的三个点分别是A(1,3),B(3,6),C(4,1).
(1)在图中画出△ABC,并作出△ABC关于y轴对称的图形△A1B1C1.
(2)将A、B、C各点横坐标、纵坐标都乘以﹣1,得A2、B2、C2,画出△A2B2C2.
( http: / / www.21cnjy.com / )
参考答案与试题解析
一.选择题(共7小题)
1.【分析】过点A作x轴的平行线DD′,作CD⊥DD′于D,作C′D′⊥DD′于D′,设C(x,y),则CD=y﹣2、AD=﹣x、C′D′=2﹣n、AD′=m,根据位似比为1:2得==,即==,计算即可.
【解答】解:过点A作x轴的平行线DD′,作CD⊥DD′于D,作C′D′⊥DD′于D′,
( http: / / www.21cnjy.com / )
设C(x,y),
则CD=y﹣2、AD=﹣x,C′D′=2﹣n,AD′=m,
∵△AB′C′与△ABC的位似比为2:1,
∴==,即==,
解得:x=﹣m,y=﹣n+3,
∴点C的坐标为(﹣m,﹣n+3),
故选:A.
2.【分析】利用位似图形 ( http: / / www.21cnjy.com )的画法:①确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;③根据位似比,确定能代表所作的位似图形的关键点;④顺次连接上述各点,得到放大或缩小的图形.【版权所有:21教育】
【解答】解:由位似图形的画法可得:前3个图形都是△ABC的位似图形.
故选:C.
3.【分析】直接利用位似图形的性质分析得出答案.
【解答】解:A、位似中心要么取在图形外部,要么取在图形内部,也可以在图形上,故此选项错误;
B、位似中心取在图形内部时,也可以把图形缩小也可以放大,故此选项错误;
C、当位似中心确定后,按要求放大或缩小的图形能画2个,故此选项错误;
D、以上说法都不正确,符合题意.
故选:D.
4.【分析】根据位似变换的定义对各选项进行判断.
【解答】解:第一个图形中的位似中心为A点,第二个图形中的位似中心为BC的中点,第三个图形中的位似中心为O点,第四个图形中的位似中心为O点.
故选:A.
5.【分析】直接利用位似图形的性质分别得出位似中心和位似比.
【解答】解:如图所示:位似中心F的坐标为:(2,2),
k的值为:=.
故选:B.
( http: / / www.21cnjy.com / )
6.【分析】连接BF交y轴于P,根据题意求出CG,根据相似三角形的性质求出GP,求出点P的坐标.
【解答】解:如图,连接BF交y轴于P,
( http: / / www.21cnjy.com / )
∵四边形ABCD和四边形EFGO是矩形,点B,F的坐标分别为(﹣4,4),(2,1),
∴点C的坐标为(0,4),点G的坐标为(0,1),
∴CG=3,
∵BC∥GF,
∴==,
∴GP=1,PC=2,
∴点P的坐标为(0,2),
故选:C.
7.【分析】利用放大2倍网格的变化进行判断.
【解答】解:原图占2×3格,则放大2倍后图形应该占4×6格,
故选:D.
二.填空题(共5小题)
8.【分析】延长BA到A1使BA1=3BA,延长BC到C1使BC1=3BC,则△A1B1C1为所作,然后写出点C1的坐标.2·1·c·n·j·y
【解答】解:如图,△A1B1C1为所作,点C的对应顶点C1的坐标是(0,﹣3).
( http: / / www.21cnjy.com / )
故答案为(0,﹣3).
9.【分析】先根据△A′B′C′与△ABC关于y轴对称,A(1,4),即可得出A'(﹣1,4),再根据以原点O为位似中心,相似比为作△A′B′C′的缩小的位似图形△A″B″C″,可得A″的坐标.【来源:21·世纪·教育·网】
【解答】解:如图所示,∵△A′B′C′与△ABC关于y轴对称,A(1,4),
∴A'(﹣1,4),
∵相似比为,
∴A“(﹣,2)或(,﹣2).
故答案为:(﹣,2)或(,﹣2).
( http: / / www.21cnjy.com / )
10.【分析】先利用矩形的性 ( http: / / www.21cnjy.com )质写出B点坐标,则根据线段中点坐标公式可写出矩形AOCB的对称中心的坐标;再利用以原点为位似中心的对应点的坐标之间的关系分别写出B1、B2、B3、B4的坐标,然后矩形A4OC4B4的对称中心的坐标.
【解答】解:∵OA=2.OC=1,
∴B(﹣2,1),
∴矩形AOCB的对称中心的坐标为(﹣1,),
∵将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,
∴B1(﹣3,),
同理可得B2(﹣,),B3(﹣,),B4(﹣,),
∴矩形A4OC4B4的对称中心的坐标是 (﹣,).
故答案为 (﹣1,),(﹣,).
11.【分析】利用位似性质和网格特点 ( http: / / www.21cnjy.com ),延长CA到A1,使CA1=2CA,延长CB到B1,使CB1=2CB,则△A1B1C1满足条件,然后写出点A1的坐标.www.21-cn-jy.com
【解答】解:如图,△A1B1C1为所作;点A1的坐标为(﹣2,﹣2).
( http: / / www.21cnjy.com / )
故答案为(﹣2,﹣2).
12.【分析】根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k,即可求得答案.
【解答】解:在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,3),21cnjy.com
∴则点A′的坐标为:(1,),
不在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,3),www-2-1-cnjy-com
∴则点A′的坐标为:(﹣1,﹣),
故答案为:(1,),(﹣1,﹣).
三.解答题(共3小题)
13.【分析】(1)利用位似图形的性质得出对应点坐标进而得出答案;
(2)根据勾股定理和三角形的面积公式即可得到结论.
【解答】解:(1)如图所示:△A'B'C'即为所求:
(2)如图所示:B'C'的长度==3;
∵A′C′=3,
∴△A′B′C′的面积为=×3×6=9平方单位,
故答案为:3,9.
( http: / / www.21cnjy.com / )
14.【分析】根据等腰三角形的性质、平行四边形的判定及相似三角形的性质求解即可得出答案.
【解答】解:①△ODA和△OCE为等腰三角形,则:
∠DOA=(180°﹣∠ODA),∠COE=(180°﹣∠OCE);
②四边形ABCD为平行四边形(理由是两组对边分别相等的四边形是平行四边形);
③∠DOA=∠COE,于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的倍得到的.
故答案为:OCE、两组对边分别相等的四边形是平行四边形,.
15.【分析】(1)先描点、连线得出△ABC,再分别作出三个顶点关于y轴的对称点,首尾顺次连接即可;2-1-c-n-j-y
(2)分别作出三个顶点关于原点的对称点,再首尾顺次连接即可.
【解答】解:(1)如图所示,△A1B1C1即为所求.
( http: / / www.21cnjy.com / )
(2)如图所示,△A2B2C2即为所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级下册
27.3.2 位似2 课后练习
一.选择题(共7小题)
1.如图,在坐标系中,以A(0, ( http: / / www.21cnjy.com )2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )
( http: / / www.21cnjy.com / )
A.(m,n+3) B.(m,n﹣3)
C.(m,n+2) D.(m,n﹣2)
2.如图所示是△ABC位似图形的几种画法,其中正确的是个数是( )
( http: / / www.21cnjy.com / )
A.1 B.2 C.3 D.4
3.用位似方法把图形扩大或缩小时,下列说法中,正确的是( )
A.位似中心要么取在图形外部,要么取在图形内部
B.位似中心取在图形内部时,只能把图形缩小
C.当位似中心确定后,按要求放大或缩小的图形只能画一个
D.以上说法都不正确
4.如图所示△DEF是△ABC位似图形的几种画法,其中正确的个数是( )
( http: / / www.21cnjy.com / )
A.4 B.3 C.2 D.1
5.如图,在平面直角坐标系中,已知点O(0, ( http: / / www.21cnjy.com )0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )21教育网
( http: / / www.21cnjy.com / )
A.(0,0),2 B.(2,2), C.(2,2),2 D.(1,1),
6.如图,矩形EFGO的两边在 ( http: / / www.21cnjy.com )坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标为( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.(0,3) B.(0,2.5) C.(0,2) D.(0,1.5)
7.如图( )图形是将已知图形按2:1放大后得到的图形.
( http: / / www.21cnjy.com / )
A.A B.B C.C D.D
二.填空题(共5小题)
8.已知△ABC在坐标平 ( http: / / www.21cnjy.com )面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以B为位似中心,画出△A1B1C1与△ABC相似,两三角形位于点B同侧且相似比是3,则点C的对应顶点C1的坐标是 .21·世纪*教育网
9.如图,△A′B′C′与△ABC关于y轴对称,已知A(1,4),B(3,1),C(3,3),若以原点O为位似中心,相似比为作△A′B′C′的缩小的位似图形△A″B″C″,则A″的坐标是 .21*cnjy*com
( http: / / www.21cnjy.com / )
10.如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA=2.OC=1,则矩形AOCB的对称中心的坐标是 ;在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2,…,按此规律,则矩形A4OC4B4的对称中心的坐标是 .21世纪教育网版权所有
( http: / / www.21cnjy.com / )
11.已知:如图△ABC ( http: / / www.21cnjy.com )三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画出△A1B1C1,使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,此时点A1的坐标为 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
12.在平面直角坐标系中,△ABC顶点A的坐 ( http: / / www.21cnjy.com )标为(2,3),若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比等于2:1,则点A′的坐标 .【出处:21教育名师】
三.解答题(共3小题)
13.如图,在由边长为1个单位的长度的小正方形组成的网格图中,已知点O及△ABC的顶点均为网格线的交点.21教育名师原创作品
(1)在给定网格中,以O为位似中心,将△ABC放大为原来的三倍,得到请△A'B'C',请画出△A'B'C';21*cnjy*com
(2)B'C'的长度为 单位长度,△A′B′C′的面积为 平方单位.
( http: / / www.21cnjy.com / )
14.放缩尺是一种绘图工具,它能把图形放大或缩小.
制作:把钻有若干等距小孔的四 ( http: / / www.21cnjy.com )根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点,OD=DA=CB,DC=AB=BE,在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:若连接OA,OE,可证得以下结论:
①△ODA和△OCE为等腰三角形,则:
∠DOA=(180°﹣∠ODA),∠COE=(180°﹣∠ );
②四边形ABCD为平行四边形(理由是 );
③∠DOA=∠COE,于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 倍得到的.
( http: / / www.21cnjy.com / )
15.如图,△ABC的三个点分别是A(1,3),B(3,6),C(4,1).
(1)在图中画出△ABC,并作出△ABC关于y轴对称的图形△A1B1C1.
(2)将A、B、C各点横坐标、纵坐标都乘以﹣1,得A2、B2、C2,画出△A2B2C2.
( http: / / www.21cnjy.com / )
参考答案与试题解析
一.选择题(共7小题)
1.【分析】过点A作x轴的平行线DD′,作CD⊥DD′于D,作C′D′⊥DD′于D′,设C(x,y),则CD=y﹣2、AD=﹣x、C′D′=2﹣n、AD′=m,根据位似比为1:2得==,即==,计算即可.
【解答】解:过点A作x轴的平行线DD′,作CD⊥DD′于D,作C′D′⊥DD′于D′,
( http: / / www.21cnjy.com / )
设C(x,y),
则CD=y﹣2、AD=﹣x,C′D′=2﹣n,AD′=m,
∵△AB′C′与△ABC的位似比为2:1,
∴==,即==,
解得:x=﹣m,y=﹣n+3,
∴点C的坐标为(﹣m,﹣n+3),
故选:A.
2.【分析】利用位似图形 ( http: / / www.21cnjy.com )的画法:①确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;③根据位似比,确定能代表所作的位似图形的关键点;④顺次连接上述各点,得到放大或缩小的图形.【版权所有:21教育】
【解答】解:由位似图形的画法可得:前3个图形都是△ABC的位似图形.
故选:C.
3.【分析】直接利用位似图形的性质分析得出答案.
【解答】解:A、位似中心要么取在图形外部,要么取在图形内部,也可以在图形上,故此选项错误;
B、位似中心取在图形内部时,也可以把图形缩小也可以放大,故此选项错误;
C、当位似中心确定后,按要求放大或缩小的图形能画2个,故此选项错误;
D、以上说法都不正确,符合题意.
故选:D.
4.【分析】根据位似变换的定义对各选项进行判断.
【解答】解:第一个图形中的位似中心为A点,第二个图形中的位似中心为BC的中点,第三个图形中的位似中心为O点,第四个图形中的位似中心为O点.
故选:A.
5.【分析】直接利用位似图形的性质分别得出位似中心和位似比.
【解答】解:如图所示:位似中心F的坐标为:(2,2),
k的值为:=.
故选:B.
( http: / / www.21cnjy.com / )
6.【分析】连接BF交y轴于P,根据题意求出CG,根据相似三角形的性质求出GP,求出点P的坐标.
【解答】解:如图,连接BF交y轴于P,
( http: / / www.21cnjy.com / )
∵四边形ABCD和四边形EFGO是矩形,点B,F的坐标分别为(﹣4,4),(2,1),
∴点C的坐标为(0,4),点G的坐标为(0,1),
∴CG=3,
∵BC∥GF,
∴==,
∴GP=1,PC=2,
∴点P的坐标为(0,2),
故选:C.
7.【分析】利用放大2倍网格的变化进行判断.
【解答】解:原图占2×3格,则放大2倍后图形应该占4×6格,
故选:D.
二.填空题(共5小题)
8.【分析】延长BA到A1使BA1=3BA,延长BC到C1使BC1=3BC,则△A1B1C1为所作,然后写出点C1的坐标.2·1·c·n·j·y
【解答】解:如图,△A1B1C1为所作,点C的对应顶点C1的坐标是(0,﹣3).
( http: / / www.21cnjy.com / )
故答案为(0,﹣3).
9.【分析】先根据△A′B′C′与△ABC关于y轴对称,A(1,4),即可得出A'(﹣1,4),再根据以原点O为位似中心,相似比为作△A′B′C′的缩小的位似图形△A″B″C″,可得A″的坐标.【来源:21·世纪·教育·网】
【解答】解:如图所示,∵△A′B′C′与△ABC关于y轴对称,A(1,4),
∴A'(﹣1,4),
∵相似比为,
∴A“(﹣,2)或(,﹣2).
故答案为:(﹣,2)或(,﹣2).
( http: / / www.21cnjy.com / )
10.【分析】先利用矩形的性 ( http: / / www.21cnjy.com )质写出B点坐标,则根据线段中点坐标公式可写出矩形AOCB的对称中心的坐标;再利用以原点为位似中心的对应点的坐标之间的关系分别写出B1、B2、B3、B4的坐标,然后矩形A4OC4B4的对称中心的坐标.
【解答】解:∵OA=2.OC=1,
∴B(﹣2,1),
∴矩形AOCB的对称中心的坐标为(﹣1,),
∵将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,
∴B1(﹣3,),
同理可得B2(﹣,),B3(﹣,),B4(﹣,),
∴矩形A4OC4B4的对称中心的坐标是 (﹣,).
故答案为 (﹣1,),(﹣,).
11.【分析】利用位似性质和网格特点 ( http: / / www.21cnjy.com ),延长CA到A1,使CA1=2CA,延长CB到B1,使CB1=2CB,则△A1B1C1满足条件,然后写出点A1的坐标.www.21-cn-jy.com
【解答】解:如图,△A1B1C1为所作;点A1的坐标为(﹣2,﹣2).
( http: / / www.21cnjy.com / )
故答案为(﹣2,﹣2).
12.【分析】根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k,即可求得答案.
【解答】解:在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,3),21cnjy.com
∴则点A′的坐标为:(1,),
不在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,3),www-2-1-cnjy-com
∴则点A′的坐标为:(﹣1,﹣),
故答案为:(1,),(﹣1,﹣).
三.解答题(共3小题)
13.【分析】(1)利用位似图形的性质得出对应点坐标进而得出答案;
(2)根据勾股定理和三角形的面积公式即可得到结论.
【解答】解:(1)如图所示:△A'B'C'即为所求:
(2)如图所示:B'C'的长度==3;
∵A′C′=3,
∴△A′B′C′的面积为=×3×6=9平方单位,
故答案为:3,9.
( http: / / www.21cnjy.com / )
14.【分析】根据等腰三角形的性质、平行四边形的判定及相似三角形的性质求解即可得出答案.
【解答】解:①△ODA和△OCE为等腰三角形,则:
∠DOA=(180°﹣∠ODA),∠COE=(180°﹣∠OCE);
②四边形ABCD为平行四边形(理由是两组对边分别相等的四边形是平行四边形);
③∠DOA=∠COE,于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的倍得到的.
故答案为:OCE、两组对边分别相等的四边形是平行四边形,.
15.【分析】(1)先描点、连线得出△ABC,再分别作出三个顶点关于y轴的对称点,首尾顺次连接即可;2-1-c-n-j-y
(2)分别作出三个顶点关于原点的对称点,再首尾顺次连接即可.
【解答】解:(1)如图所示,△A1B1C1即为所求.
( http: / / www.21cnjy.com / )
(2)如图所示,△A2B2C2即为所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
