【精品原创】人教版数学九年级下册 27.4.1《相似章末复习》练习(含答案)
文档属性
| 名称 | 【精品原创】人教版数学九年级下册 27.4.1《相似章末复习》练习(含答案) | 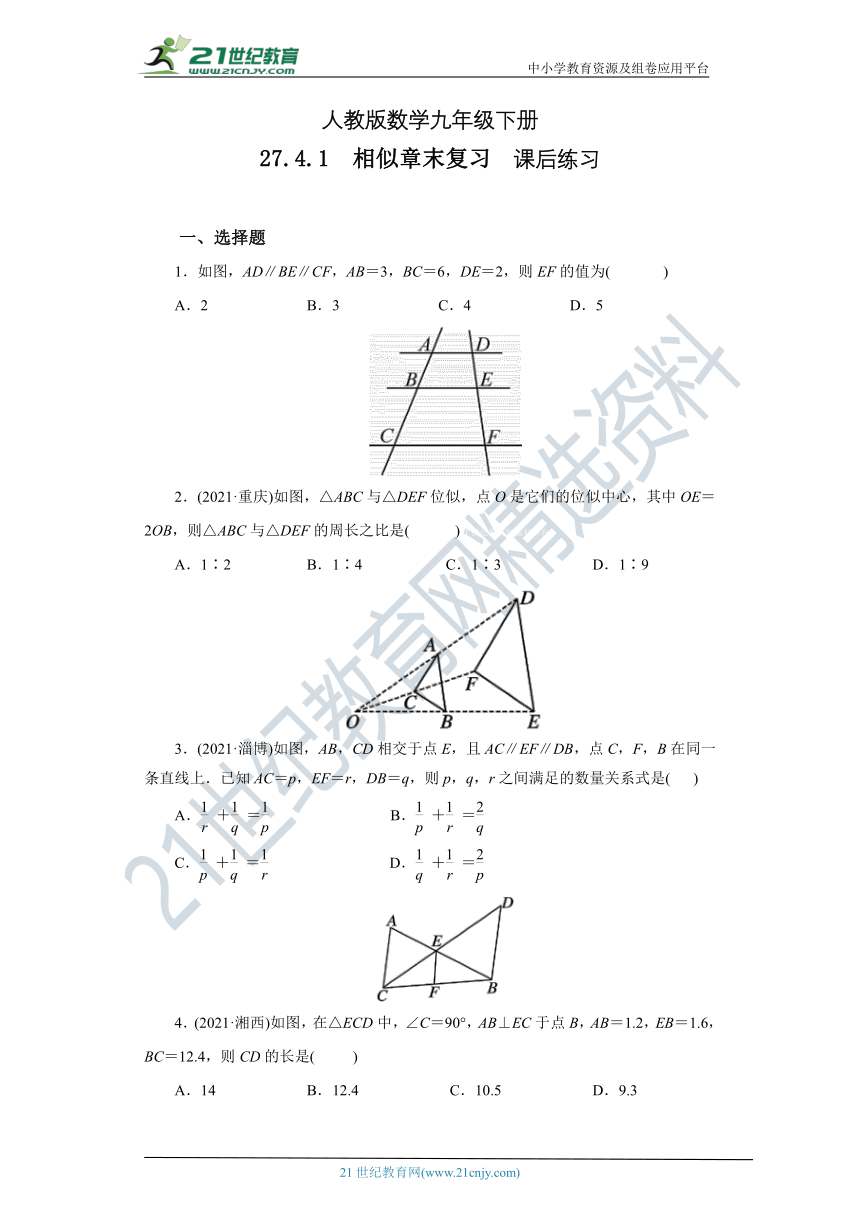 | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:41 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册
27.4.1 相似章末复习 课后练习
一、选择题
1.如图,AD∥BE∥CF,AB=3,BC=6,DE=2,则EF的值为( )
A.2 B.3 C.4 D.5
( http: / / www.21cnjy.com / )
2.(2021·重庆)如图 ( http: / / www.21cnjy.com ),△ABC与△DEF位似,点O是它们的位似中心,其中OE=2OB,则△ABC与△DEF的周长之比是( )21世纪教育网版权所有
A.1∶2 B.1∶4 C.1∶3 D.1∶9
( http: / / www.21cnjy.com / )
3.(2021·淄博)如 ( http: / / www.21cnjy.com )图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上.已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
A.+= B.+=
C.+= D.+=
( http: / / www.21cnjy.com / )
4.(2021·湘西)如 ( http: / / www.21cnjy.com )图,在△ECD中,∠C=90°,AB⊥EC于点B,AB=1.2,EB=1.6,BC=12.4,则CD的长是( )21教育网
A.14 B.12.4 C.10.5 D.9.3
( http: / / www.21cnjy.com / )
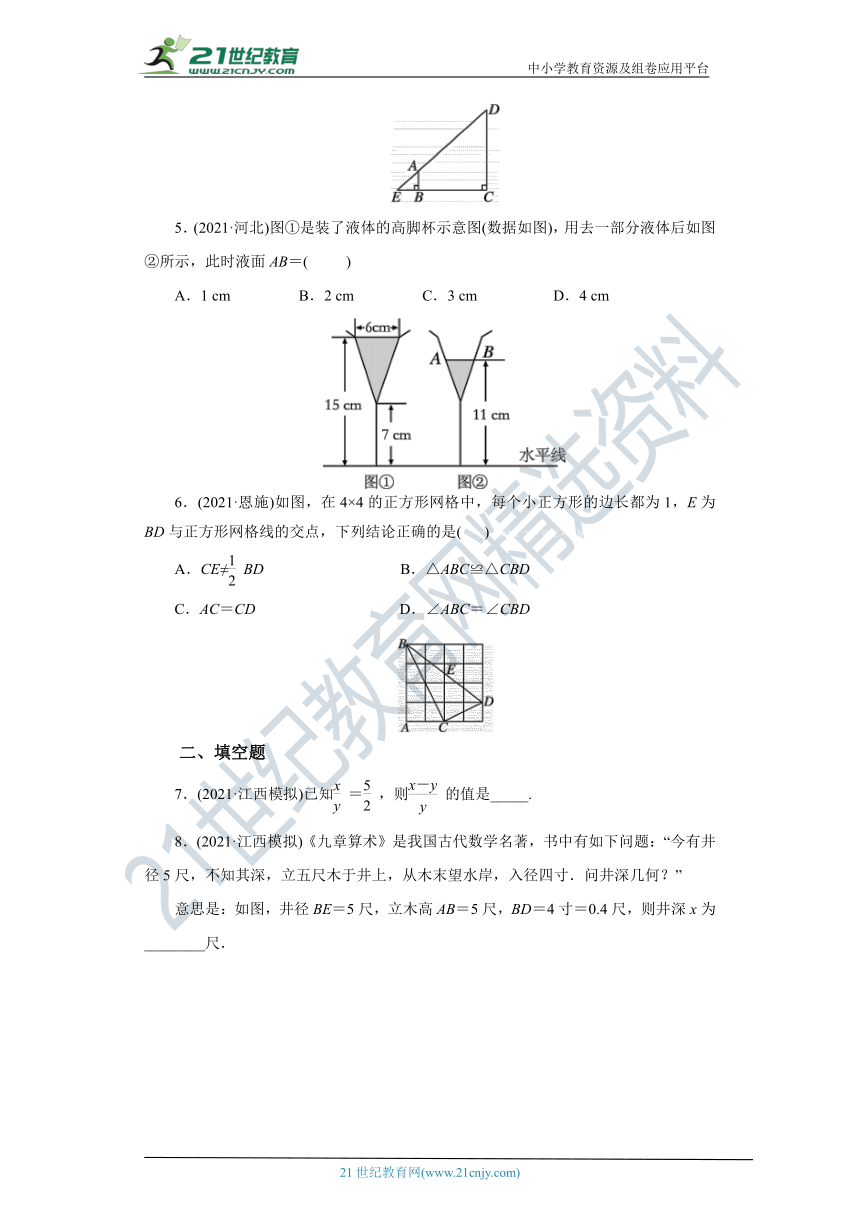
5.(2021·河北)图①是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图②所示,此时液面AB=( )21cnjy.com
A.1 cm B.2 cm C.3 cm D.4 cm
( http: / / www.21cnjy.com / )
6.(2021·恩施)如图,在4×4的正方形网格中,每个小正方形的边长都为1,E为BD与正方形网格线的交点,下列结论正确的是( )【来源:21·世纪·教育·网】
A.CE≠BD B.△ABC≌△CBD
C.AC=CD D.∠ABC=∠CBD
( http: / / www.21cnjy.com / )
二、填空题
7.(2021·江西模拟)已知=,则的值是_____.
8.(2021·江西模拟)《九章算术》是我国 ( http: / / www.21cnjy.com )古代数学名著,书中有如下问题:“今有井径5尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸.问井深几何?”
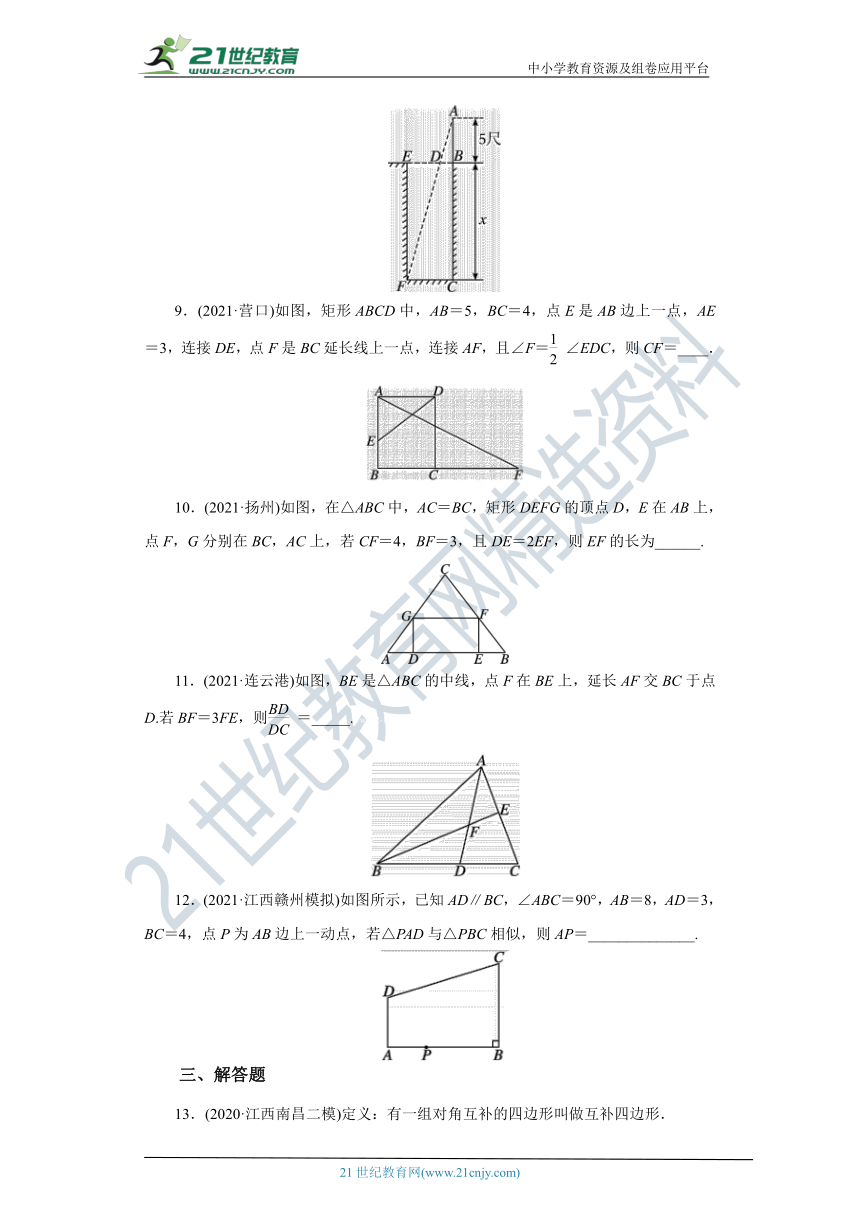
意思是:如图,井径BE=5尺,立木高AB=5尺,BD=4寸=0.4尺,则井深x为________尺.21·世纪*教育网
( http: / / www.21cnjy.com / )
9.(2021·营口)如图,矩形AB ( http: / / www.21cnjy.com )CD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且∠F=∠EDC,则CF=____.
( http: / / www.21cnjy.com / )
10.(2021·扬州)如图,在△A ( http: / / www.21cnjy.com )BC中,AC=BC,矩形DEFG的顶点D,E在AB上,点F,G分别在BC,AC上,若CF=4,BF=3,且DE=2EF,则EF的长为______.
( http: / / www.21cnjy.com / )
11.(2021·连云港)如图,BE是△ABC的中线,点F在BE上,延长AF交BC于点D.若BF=3FE,则=_____.www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
12.(2021·江西赣州 ( http: / / www.21cnjy.com )模拟)如图所示,已知AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC相似,则AP=______________.
( http: / / www.21cnjy.com / )
三、解答题
13.(2020·江西南昌二模)定义:有一组对角互补的四边形叫做互补四边形.
(1)概念理解:
①在互补四边形ABCD中,∠A与∠C是一组对角,若∠B∶∠C∶∠D=2∶3∶4,则∠A=________°;21·cn·jy·com
②如图①,在△ABC中,点D,E分别在边AB,BC上,且BE·BC=AB·BD,求证:四边形ADEC是互补四边形.2·1·c·n·j·y
(2)探究发现:如图②,在 ( http: / / www.21cnjy.com )等腰△ABE中,AE=BE,点C,D分别在边BE,AE上,AD=BC,四边形CEDH是互补四边形,求证:∠ABD=∠BAC=∠E.
(3)推广运用:如图③,在△A ( http: / / www.21cnjy.com )BE中,点C,D分别在边BE,AE上,AD=BC,四边形CEDH是互补四边形,若∠E=60°,AB=6,AE=,求的值.
( http: / / www.21cnjy.com / )
参考答案
1.答案:C
2.答案:A
3.答案:C
4.答案:C
5.答案:C
6.答案:D
7.答案:
8.答案:57.5
9.答案:6
10.答案:
11.答案:
12.答案:或2或6
13.(1)①90;
②证明:∵BE·BC=AB·BD,∴=,
又∵∠B=∠B,∴△BDE∽△BCA,
∴∠BED=∠A,∴∠A+∠CED=∠BED+∠CED=180°,
∴四边形ADEC是互补四边形;
(2)证明:可证△EAC≌△EBD(SAS),∴∠EBD=∠EAC.
∵AE=BE,∴∠EAB=∠EBA,∴∠ABD=∠BAC,
∵四边形CEDH是互补四边形,∴∠E+∠DHC=180°,
∵∠AHB=∠DHC,∴∠E+∠AHB=180°,
∴∠ABD+∠BAC=∠E,∴∠ABD=∠BAC=∠E;
(3)解:作BF⊥HC于点F,AG⊥HD交HD的延长线于点G,可证△ADG≌△BCF(AAS),Rt△ABG≌Rt△BAF(HL),www.21-cn-jy.com
∴∠HAB=∠HBA=∠E=30°,
在Rt△AGH中,∠AHG=∠HAB+∠HBA=60°,
∴∠GAH=30°,
设GH=x,则AG=x,AH=2x,∴AB=2AG=2x=6,
∴x=,∴AH=2,
∵∠DAH=∠CAE,∠DHA=∠E=60°,
∴△ADH∽△ACE,
∴==.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级下册
27.4.1 相似章末复习 课后练习
一、选择题
1.如图,AD∥BE∥CF,AB=3,BC=6,DE=2,则EF的值为( )
A.2 B.3 C.4 D.5
( http: / / www.21cnjy.com / )
2.(2021·重庆)如图 ( http: / / www.21cnjy.com ),△ABC与△DEF位似,点O是它们的位似中心,其中OE=2OB,则△ABC与△DEF的周长之比是( )21世纪教育网版权所有
A.1∶2 B.1∶4 C.1∶3 D.1∶9
( http: / / www.21cnjy.com / )
3.(2021·淄博)如 ( http: / / www.21cnjy.com )图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上.已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
A.+= B.+=
C.+= D.+=
( http: / / www.21cnjy.com / )
4.(2021·湘西)如 ( http: / / www.21cnjy.com )图,在△ECD中,∠C=90°,AB⊥EC于点B,AB=1.2,EB=1.6,BC=12.4,则CD的长是( )21教育网
A.14 B.12.4 C.10.5 D.9.3
( http: / / www.21cnjy.com / )
5.(2021·河北)图①是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图②所示,此时液面AB=( )21cnjy.com
A.1 cm B.2 cm C.3 cm D.4 cm
( http: / / www.21cnjy.com / )
6.(2021·恩施)如图,在4×4的正方形网格中,每个小正方形的边长都为1,E为BD与正方形网格线的交点,下列结论正确的是( )【来源:21·世纪·教育·网】
A.CE≠BD B.△ABC≌△CBD
C.AC=CD D.∠ABC=∠CBD
( http: / / www.21cnjy.com / )
二、填空题
7.(2021·江西模拟)已知=,则的值是_____.
8.(2021·江西模拟)《九章算术》是我国 ( http: / / www.21cnjy.com )古代数学名著,书中有如下问题:“今有井径5尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸.问井深几何?”
意思是:如图,井径BE=5尺,立木高AB=5尺,BD=4寸=0.4尺,则井深x为________尺.21·世纪*教育网
( http: / / www.21cnjy.com / )
9.(2021·营口)如图,矩形AB ( http: / / www.21cnjy.com )CD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且∠F=∠EDC,则CF=____.
( http: / / www.21cnjy.com / )
10.(2021·扬州)如图,在△A ( http: / / www.21cnjy.com )BC中,AC=BC,矩形DEFG的顶点D,E在AB上,点F,G分别在BC,AC上,若CF=4,BF=3,且DE=2EF,则EF的长为______.
( http: / / www.21cnjy.com / )
11.(2021·连云港)如图,BE是△ABC的中线,点F在BE上,延长AF交BC于点D.若BF=3FE,则=_____.www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
12.(2021·江西赣州 ( http: / / www.21cnjy.com )模拟)如图所示,已知AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC相似,则AP=______________.
( http: / / www.21cnjy.com / )
三、解答题
13.(2020·江西南昌二模)定义:有一组对角互补的四边形叫做互补四边形.
(1)概念理解:
①在互补四边形ABCD中,∠A与∠C是一组对角,若∠B∶∠C∶∠D=2∶3∶4,则∠A=________°;21·cn·jy·com
②如图①,在△ABC中,点D,E分别在边AB,BC上,且BE·BC=AB·BD,求证:四边形ADEC是互补四边形.2·1·c·n·j·y
(2)探究发现:如图②,在 ( http: / / www.21cnjy.com )等腰△ABE中,AE=BE,点C,D分别在边BE,AE上,AD=BC,四边形CEDH是互补四边形,求证:∠ABD=∠BAC=∠E.
(3)推广运用:如图③,在△A ( http: / / www.21cnjy.com )BE中,点C,D分别在边BE,AE上,AD=BC,四边形CEDH是互补四边形,若∠E=60°,AB=6,AE=,求的值.
( http: / / www.21cnjy.com / )
参考答案
1.答案:C
2.答案:A
3.答案:C
4.答案:C
5.答案:C
6.答案:D
7.答案:
8.答案:57.5
9.答案:6
10.答案:
11.答案:
12.答案:或2或6
13.(1)①90;
②证明:∵BE·BC=AB·BD,∴=,
又∵∠B=∠B,∴△BDE∽△BCA,
∴∠BED=∠A,∴∠A+∠CED=∠BED+∠CED=180°,
∴四边形ADEC是互补四边形;
(2)证明:可证△EAC≌△EBD(SAS),∴∠EBD=∠EAC.
∵AE=BE,∴∠EAB=∠EBA,∴∠ABD=∠BAC,
∵四边形CEDH是互补四边形,∴∠E+∠DHC=180°,
∵∠AHB=∠DHC,∴∠E+∠AHB=180°,
∴∠ABD+∠BAC=∠E,∴∠ABD=∠BAC=∠E;
(3)解:作BF⊥HC于点F,AG⊥HD交HD的延长线于点G,可证△ADG≌△BCF(AAS),Rt△ABG≌Rt△BAF(HL),www.21-cn-jy.com
∴∠HAB=∠HBA=∠E=30°,
在Rt△AGH中,∠AHG=∠HAB+∠HBA=60°,
∴∠GAH=30°,
设GH=x,则AG=x,AH=2x,∴AB=2AG=2x=6,
∴x=,∴AH=2,
∵∠DAH=∠CAE,∠DHA=∠E=60°,
∴△ADH∽△ACE,
∴==.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
