【精品原创】人教版数学九年级下册 28.2.2.2 《利用仰俯角解直角三角形》练习(含答案)
文档属性
| 名称 | 【精品原创】人教版数学九年级下册 28.2.2.2 《利用仰俯角解直角三角形》练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 16:08:41 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册
28.2.2.2 利用仰俯角解直角三角形 课后练习
一、单选题
1.如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
( http: / / www.21cnjy.com / )
A.6sin 75°米 B.米 C.米 D.6tan 75°米
2.如图,在水平地面上,由点A测得旗杆BC的顶点C的仰角为60°,点A到旗杆底部的距离AB=12米,则旗杆的高度为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A.6米 B.6米 C.12米 D.12米
3.如图,AB,CD两教学楼相距30米,某 ( http: / / www.21cnjy.com )学生在教室窗台口B处得CD楼楼顶C处的仰角为30°,楼底D处的俯角为45°,则教学楼CD的高度为( )
( http: / / www.21cnjy.com / )
A.(10+30)米 B.(30-)米 C.45米 D.5米
4.某飞机的飞行高度为1500米,从飞机上测得地面控制点的俯角为60°,此时飞机与地面控制点的距离为____米.21cnjy.com
二、填空题
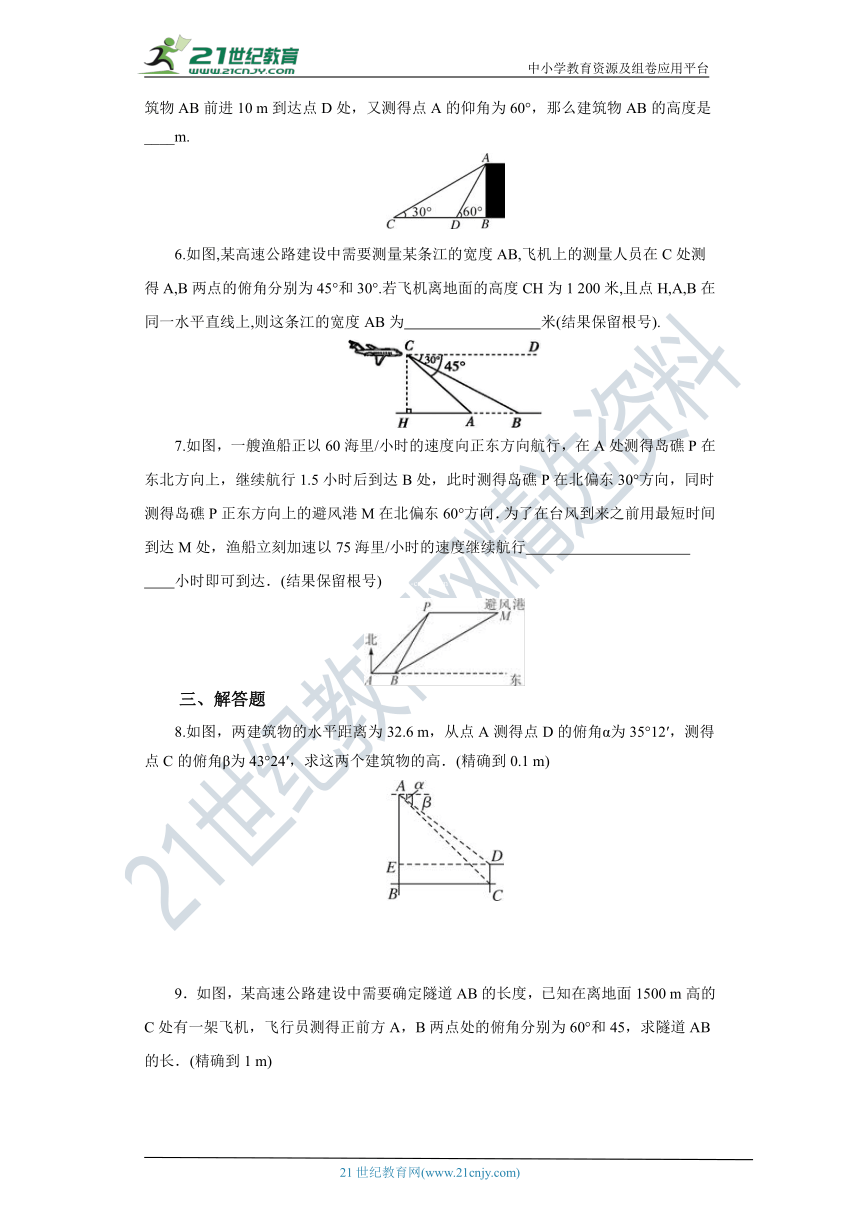
5.某中学初三年级的学生开展测量物体高 ( http: / / www.21cnjy.com )度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进10 m到达点D处,又测得点A的仰角为60°,那么建筑物AB的高度是____m. 21·cn·jy·com
( http: / / www.21cnjy.com / )
6.如图,某高速公路建设中需要测量 ( http: / / www.21cnjy.com )某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1 200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为 米(结果保留根号).
( http: / / www.21cnjy.com / )
7.如图,一艘渔船正以60海里/小 ( http: / / www.21cnjy.com )时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行 小时即可到达.(结果保留根号)www.21-cn-jy.com
( http: / / www.21cnjy.com / )
三、解答题
8.如图,两建筑物的水平距离为3 ( http: / / www.21cnjy.com )2.6 m,从点A测得点D的俯角α为35°12′,测得点C的俯角β为43°24′,求这两个建筑物的高.(精确到0.1 m)2·1·c·n·j·y
( http: / / www.21cnjy.com / )
9.如图,某高速公路建设中需要确定隧道AB的长度,已知在离地面1500 m高的C处有一架飞机,飞行员测得正前方A,B两点处的俯角分别为60°和45,求隧道AB的长.(精确到1 m)【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
10.如图,某大楼顶部有一旗杆AB,甲乙两人分别在相距6米的C、D两处测得B点和A点的仰角分别是42°和65°,且C、D、E在一条直线上.如果DE=15米,求旗杆AB的长大约是多少米?(结果保留整数,参考数据:sin 42°≈0.67,tan 42°≈0.9,sin 65°≈0.91,tan 65°≈2.1)21教育网
( http: / / www.21cnjy.com / )
参考答案
1. D
2. C
3. A
4. 1000
5. 5
6.1200(-1)
7.
8. 解:根据题意,得∠ACB=β=43°24′,∠ADE=α=35°12′,DE=BC=32.6 m.
在Rt△ABC中,
∵tan∠ACB=,
∴AB=BC·tan∠ACB=32.6×tan 43°24′≈30.83(m).
在Rt△ADE中,∵tan∠ADE=,
∴AE=DE·tan∠ADE=32.6×tan 35°12′≈23.00(m).
∴DC=BE=AB-AE=30.83-23.00≈7.8(m).
即两个建筑物的高分别约为30.8 m、7.8 m.
9.解:过C作CO⊥AB于O,则CO=1500 m,
由题意知:∠CBO=45°,∠CAO=60°,
在Rt△CBO中,
OB===1500,OA===500,
∴AB=OB-OA=1500-500≈634(m).
答:隧道AB的长约为634 m.
10.解:在Rt△ADE中,∠ADE=65°,DE=15米,
则tan∠ADE=,
即tan 65°=≈2.1,
解得 AE≈31.5米.
在Rt△BCE中,
∠BCE=42°,CE=CD+DE=21米,
∴tan∠BCE=,即tan 42°=≈0.9,
解得 BE≈18.9米.
∴AB=AE-BE=31.5-18.9≈13(米).
即旗杆AB的长大约是13米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级下册
28.2.2.2 利用仰俯角解直角三角形 课后练习
一、单选题
1.如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
( http: / / www.21cnjy.com / )
A.6sin 75°米 B.米 C.米 D.6tan 75°米
2.如图,在水平地面上,由点A测得旗杆BC的顶点C的仰角为60°,点A到旗杆底部的距离AB=12米,则旗杆的高度为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A.6米 B.6米 C.12米 D.12米
3.如图,AB,CD两教学楼相距30米,某 ( http: / / www.21cnjy.com )学生在教室窗台口B处得CD楼楼顶C处的仰角为30°,楼底D处的俯角为45°,则教学楼CD的高度为( )
( http: / / www.21cnjy.com / )
A.(10+30)米 B.(30-)米 C.45米 D.5米
4.某飞机的飞行高度为1500米,从飞机上测得地面控制点的俯角为60°,此时飞机与地面控制点的距离为____米.21cnjy.com
二、填空题
5.某中学初三年级的学生开展测量物体高 ( http: / / www.21cnjy.com )度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进10 m到达点D处,又测得点A的仰角为60°,那么建筑物AB的高度是____m. 21·cn·jy·com
( http: / / www.21cnjy.com / )
6.如图,某高速公路建设中需要测量 ( http: / / www.21cnjy.com )某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1 200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为 米(结果保留根号).
( http: / / www.21cnjy.com / )
7.如图,一艘渔船正以60海里/小 ( http: / / www.21cnjy.com )时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行 小时即可到达.(结果保留根号)www.21-cn-jy.com
( http: / / www.21cnjy.com / )
三、解答题
8.如图,两建筑物的水平距离为3 ( http: / / www.21cnjy.com )2.6 m,从点A测得点D的俯角α为35°12′,测得点C的俯角β为43°24′,求这两个建筑物的高.(精确到0.1 m)2·1·c·n·j·y
( http: / / www.21cnjy.com / )
9.如图,某高速公路建设中需要确定隧道AB的长度,已知在离地面1500 m高的C处有一架飞机,飞行员测得正前方A,B两点处的俯角分别为60°和45,求隧道AB的长.(精确到1 m)【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
10.如图,某大楼顶部有一旗杆AB,甲乙两人分别在相距6米的C、D两处测得B点和A点的仰角分别是42°和65°,且C、D、E在一条直线上.如果DE=15米,求旗杆AB的长大约是多少米?(结果保留整数,参考数据:sin 42°≈0.67,tan 42°≈0.9,sin 65°≈0.91,tan 65°≈2.1)21教育网
( http: / / www.21cnjy.com / )
参考答案
1. D
2. C
3. A
4. 1000
5. 5
6.1200(-1)
7.
8. 解:根据题意,得∠ACB=β=43°24′,∠ADE=α=35°12′,DE=BC=32.6 m.
在Rt△ABC中,
∵tan∠ACB=,
∴AB=BC·tan∠ACB=32.6×tan 43°24′≈30.83(m).
在Rt△ADE中,∵tan∠ADE=,
∴AE=DE·tan∠ADE=32.6×tan 35°12′≈23.00(m).
∴DC=BE=AB-AE=30.83-23.00≈7.8(m).
即两个建筑物的高分别约为30.8 m、7.8 m.
9.解:过C作CO⊥AB于O,则CO=1500 m,
由题意知:∠CBO=45°,∠CAO=60°,
在Rt△CBO中,
OB===1500,OA===500,
∴AB=OB-OA=1500-500≈634(m).
答:隧道AB的长约为634 m.
10.解:在Rt△ADE中,∠ADE=65°,DE=15米,
则tan∠ADE=,
即tan 65°=≈2.1,
解得 AE≈31.5米.
在Rt△BCE中,
∠BCE=42°,CE=CD+DE=21米,
∴tan∠BCE=,即tan 42°=≈0.9,
解得 BE≈18.9米.
∴AB=AE-BE=31.5-18.9≈13(米).
即旗杆AB的长大约是13米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
