高一下学期物理人教版(2019)必修第二册 6.4 生活中的圆周运动 课件(共48张PPT)
文档属性
| 名称 | 高一下学期物理人教版(2019)必修第二册 6.4 生活中的圆周运动 课件(共48张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-22 19:24:22 | ||
图片预览









文档简介
(共48张PPT)
6.4 生活中的圆周运动
(一)
F向
一.铁路的弯道
火车车轮介绍
F
轮缘
外轨
内轨
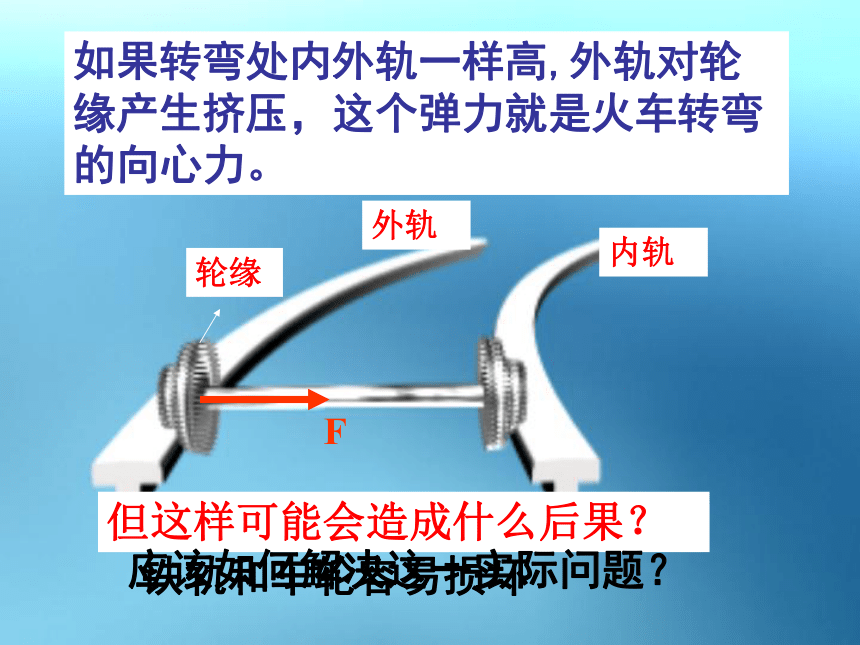
如果转弯处内外轨一样高,外轨对轮缘产生挤压,这个弹力就是火车转弯的向心力。
但这样可能会造成什么后果?
铁轨和车轮容易损坏
应该如何解决这一实际问题?
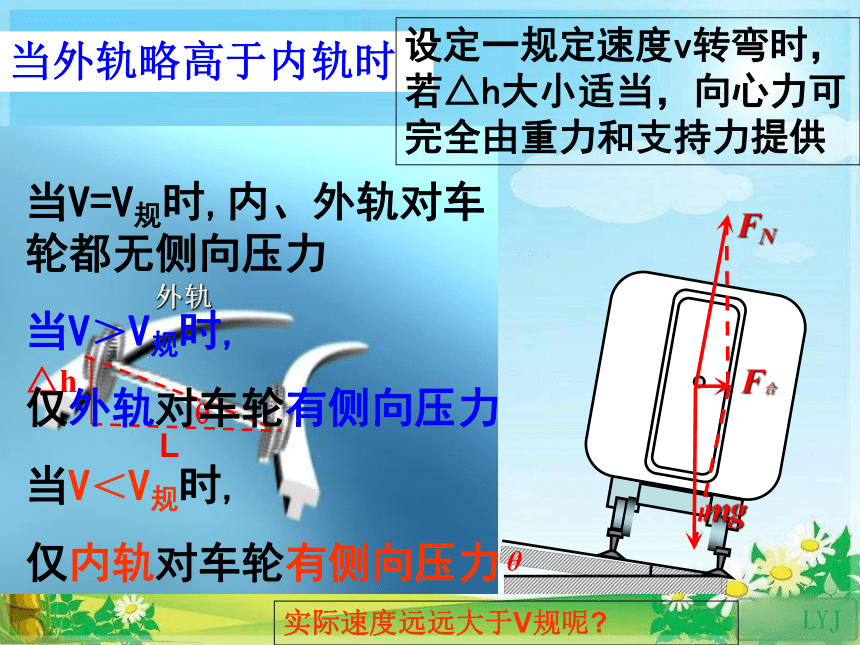
当外轨略高于内轨时
θ
FN
mg
F合
△h
外轨
L
当V=V规时,内、外轨对车轮都无侧向压力
当V>V规时,
仅外轨对车轮有侧向压力
当V<V规时,
仅内轨对车轮有侧向压力
设定一规定速度v转弯时,若△h大小适当,向心力可完全由重力和支持力提供
实际速度远远大于V规呢
赛道的设计
二、拱形桥
设车质量为m,过最高点的速度为v,且设凸形路面对应的圆弧半径为R,则车在最高点时对地面的压力多大?
v
R
O
v
R
O
mg
FN
可见,汽车对桥的压力FN小于汽车的重力mg,并且压力随汽车速度的增大而减少。
失重现象
根据牛顿第三定律,车对地面的压力:
FN`=FN=mg - mv2/r
O
R
v
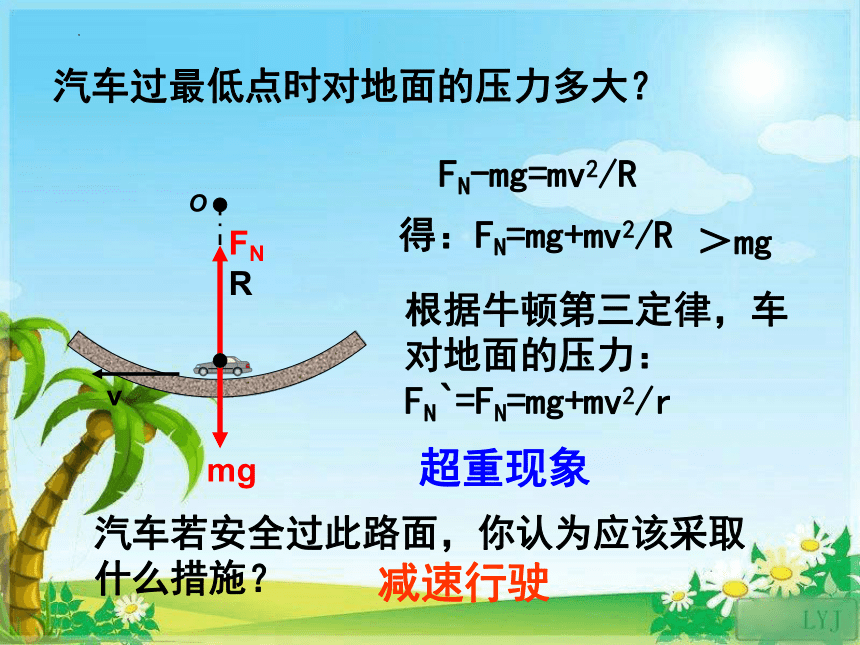
汽车过最低点时对地面的压力多大?
mg
FN
FN-mg=mv2/R
得:FN=mg+mv2/R
>mg
根据牛顿第三定律,车对地面的压力:FN`=FN=mg+mv2/r
超重现象
汽车若安全过此路面,你认为应该采取什么措施?
减速行驶
一辆卡车在丘陵地区行驶(假设卡车的速率恒定),地形如下图所示,由于轮胎太旧,途中爆胎,爆胎可能性最大的地段应是( )
A.a处 B.b处
C.c处 D.d处
a
c
b
d
1.如图所示,将完全相同的两小球A、B用长L=0.8m的细绳,悬于以v =4m/s向右匀速运动的小车顶部,两球的小车前后壁接触。由于某种原因,小车突然停止,此时悬线中张力之比TB:TA为(g=10m/s2) ( )
A.1:1 B.1:2 C.1:3 D.1:4
2.质量为25Kg 的小孩坐在秋千板上,绳长2.5m,如果秋千摆到最低点时,小孩的速度为0.5m/s,则小孩对秋千板的压力是多大?
3.在水平圆盘上分别放甲、乙、丙三个质量m的物体,其轨道半径分别为r、2r、3r如图所示,三个物体的最大静擦力皆为所受重力的k倍,当圆盘角速度由小缓慢增加,相对圆盘首先滑动的是:( )
A、甲物体 B、乙物体
C、丙物体 D、三个物体同时滑动
2. 如果甲、乙、丙质量分别
为m 、2m 、3m呢?
小结
一.铁路的弯道
当外轨略高于内轨时
当V=V规时,内、外轨对车轮都无侧向压力
当V>V规时,仅外轨对车轮有侧向压力
当V<V规时,仅内轨对车轮有侧向压力
二、拱形桥
v
R
O
mg
FN
失重现象
O
R
v
mg
FN
FN-mg=mv2/R
超重现象
作业本:P15 1-6
生活中的圆周运动
(二)
复习
拱形桥
v
R
O
mg
FN
失重现象
O
R
v
mg
FN
FN-mg=mv2/R
超重现象
思考:
地球可以看做一个巨大的拱行桥,桥面的半径是地球半径
(约为6400km)。地面上有一辆车,假设可以不断加
速,会不会出现这样的情况:速度大到一定程度时,地面
对车的支持力是0?
那此时车里的驾驶员受到的支持力为多少?
三、航天器中的失重现象
mg
FN
对宇航员:
FN = 0,宇航员处于完全失重状态
r
三、离心运动
2、离心运动方向:
1、物体做离心运动的条件:
沿切线方向。
远离圆心。
F
“供需”平衡 物体做匀速圆周运动
提供物体做匀速圆周运动的力
物体做匀速圆周运动所需的力
向心力公式的理解
=
从“供” “需”两方面研究做圆周运动的物体
三、离心运动 应用
1、脱水桶
利用离心运动把附着在衣服上的水分甩掉的装置
解释:
当脱水桶转得比较慢时,水滴跟衣服的附着力F足以提供所需的向心力,使水滴做圆周运动。当桶转得比较快时,附着力 F 不足以提供所需的向心力,于是水滴做离心运动,穿过桶孔,飞到外面。
2、用离心机把体温计的水银柱甩回玻璃泡内
当离心机转得比较慢时,缩口的阻力 F 足以提供所需的向心力,缩口上方的水银柱做圆周运动。当离心机转得相当快时,阻力 F 不足以提供所需的向心力,水银柱做离心运动而进入玻璃泡内。
3、制作“棉花”糖的原理:
内筒与洗衣机的脱水筒相似,里面加入白砂糖,加热使糖熔化成糖汁。内筒高速旋转,黏稠的糖汁就做离心运动,从内筒壁的小孔飞散出去,成为丝状到达温度较低的外筒,并迅速冷却凝固,变得纤细雪白,像一团团棉花。
4、离心分离器的原理:
可以将固体和液体分离开来。
质量大的固体需要的向心力比液体大,“远离圆心的程度”比液体明显。
三、离心运动 的危害
汽车转弯为什么会翻车?
竖直平面内的圆周运动
研究与讨论
2、有无可能做这样的运动?若可能应满足怎样的条件?
G
FN
问题1:绳球模型
用长为L的细绳拴着质量为m的小球,使小球在竖直平面内做圆周运动,如图所示。
o
A
L
v1
B
v2
试分析:
(1)当小球在最低点A的速度为v1时,其绳的张力为多大?
(2)当小球在最高点B的速度为v2 时,其绳的张力与速度的关系怎样?
v1
o
mg
F2
mg
F1
思考:过最高点的最小速度是多大
(1)当F=0时,速度v为最小值
最低点:
最高点:
v2
拓展:物体沿竖直内轨运动
有一个竖直放置的内壁光滑圆环,其半径为R,质量为m的小球沿它的内表面做圆周运动,分析小球在最高点A的速度应满足什么条件?
v
A
mg
FN
A
明确:向心力和向心加速度公式同样适合于变速圆周运动,但求质点在圆周上某点的向心力和向心加速度的大小,必须用该点的瞬时速度值。
小结:
实例一:水流星
思考: 在“水流星”的表演中,杯子在竖直面内做圆周运动,到最高点时,杯口朝下,但杯中的水却不会流下来,为什么呢?
作圆周运动的物体总需要向心力。当杯子以速度v 转过最高点时,杯中的水受力如图所示。
对杯中的水:
G
FN
由此可知,v 越大,杯子底对水的压力越大。
FN = 0
此时水恰好不流出。
表演“水流星”节目的演员,需要保证杯子在圆周运动最高点的线速度不得小于
即∶
思考:过山车为什么在最高点也不会掉下来?
实例二:过山车
G
FN
FN = 0
要想保证过山车在最高点不掉下来,此时速度
问题2:杆物模型:
用长为L的轻杆一端固定着一个质量为m的小球,使小球在竖直平面内做圆周运动,如图所示。
试分析:
(1)当小球在最低点A的速度为v2时,杆的受力与速度的关系怎样?
(2)当小球在最高点B的速度为v1时,杆的受力与速度的关系怎样?
A
B
F3
mg
F1
mg
F2
v1
v2
o
思考:过最高点的最小速度是多大 何时杆子表现为拉力,何时表现为支持力
问题2:杆物模型:
A
B
拓展:物体在管型轨道内的运动
如图,有一内壁光滑竖直放置的管型轨道半径为R,内有一质量为m的小球,沿其竖直方向上的做变速圆周运动,小球的直径刚好与管的内径相等
(1)小球在运动到最高点的时候速度与受力的关系是怎样的?
(2)小球运动到最低点的时候速度与受力的关系又是怎样?
G
V1(V2)
A
G
F3
V3
分析:
F1
F2
R
最高点:
;
最低点:
思考:小球在最高点的最小速度可以是多少?什么时候外管壁对小球有压力,什么时候内管壁对小球有支持力 什么时候内外管壁都没有压力?
(1)最高点最小速度
(2)当
时,管壁对小球没有力的作用
时,外管壁对小球有作用力
(3)当
V >
时,内管壁对小球有作用力
(4)当
V <
长为0.6 m的轻杆OA(不计质量), A端插个质量为2.0 kg的物体,在竖直平面内绕O点做圆周运动,当球达到最高点的速度分别为3 m/s, m/s, 2 m/s时, 求杆对球的作用力各为多少
O
A
巩固应用:
6.4 生活中的圆周运动
(一)
F向
一.铁路的弯道
火车车轮介绍
F
轮缘
外轨
内轨
如果转弯处内外轨一样高,外轨对轮缘产生挤压,这个弹力就是火车转弯的向心力。
但这样可能会造成什么后果?
铁轨和车轮容易损坏
应该如何解决这一实际问题?
当外轨略高于内轨时
θ
FN
mg
F合
△h
外轨
L
当V=V规时,内、外轨对车轮都无侧向压力
当V>V规时,
仅外轨对车轮有侧向压力
当V<V规时,
仅内轨对车轮有侧向压力
设定一规定速度v转弯时,若△h大小适当,向心力可完全由重力和支持力提供
实际速度远远大于V规呢
赛道的设计
二、拱形桥
设车质量为m,过最高点的速度为v,且设凸形路面对应的圆弧半径为R,则车在最高点时对地面的压力多大?
v
R
O
v
R
O
mg
FN
可见,汽车对桥的压力FN小于汽车的重力mg,并且压力随汽车速度的增大而减少。
失重现象
根据牛顿第三定律,车对地面的压力:
FN`=FN=mg - mv2/r
O
R
v
汽车过最低点时对地面的压力多大?
mg
FN
FN-mg=mv2/R
得:FN=mg+mv2/R
>mg
根据牛顿第三定律,车对地面的压力:FN`=FN=mg+mv2/r
超重现象
汽车若安全过此路面,你认为应该采取什么措施?
减速行驶
一辆卡车在丘陵地区行驶(假设卡车的速率恒定),地形如下图所示,由于轮胎太旧,途中爆胎,爆胎可能性最大的地段应是( )
A.a处 B.b处
C.c处 D.d处
a
c
b
d
1.如图所示,将完全相同的两小球A、B用长L=0.8m的细绳,悬于以v =4m/s向右匀速运动的小车顶部,两球的小车前后壁接触。由于某种原因,小车突然停止,此时悬线中张力之比TB:TA为(g=10m/s2) ( )
A.1:1 B.1:2 C.1:3 D.1:4
2.质量为25Kg 的小孩坐在秋千板上,绳长2.5m,如果秋千摆到最低点时,小孩的速度为0.5m/s,则小孩对秋千板的压力是多大?
3.在水平圆盘上分别放甲、乙、丙三个质量m的物体,其轨道半径分别为r、2r、3r如图所示,三个物体的最大静擦力皆为所受重力的k倍,当圆盘角速度由小缓慢增加,相对圆盘首先滑动的是:( )
A、甲物体 B、乙物体
C、丙物体 D、三个物体同时滑动
2. 如果甲、乙、丙质量分别
为m 、2m 、3m呢?
小结
一.铁路的弯道
当外轨略高于内轨时
当V=V规时,内、外轨对车轮都无侧向压力
当V>V规时,仅外轨对车轮有侧向压力
当V<V规时,仅内轨对车轮有侧向压力
二、拱形桥
v
R
O
mg
FN
失重现象
O
R
v
mg
FN
FN-mg=mv2/R
超重现象
作业本:P15 1-6
生活中的圆周运动
(二)
复习
拱形桥
v
R
O
mg
FN
失重现象
O
R
v
mg
FN
FN-mg=mv2/R
超重现象
思考:
地球可以看做一个巨大的拱行桥,桥面的半径是地球半径
(约为6400km)。地面上有一辆车,假设可以不断加
速,会不会出现这样的情况:速度大到一定程度时,地面
对车的支持力是0?
那此时车里的驾驶员受到的支持力为多少?
三、航天器中的失重现象
mg
FN
对宇航员:
FN = 0,宇航员处于完全失重状态
r
三、离心运动
2、离心运动方向:
1、物体做离心运动的条件:
沿切线方向。
远离圆心。
F
“供需”平衡 物体做匀速圆周运动
提供物体做匀速圆周运动的力
物体做匀速圆周运动所需的力
向心力公式的理解
=
从“供” “需”两方面研究做圆周运动的物体
三、离心运动 应用
1、脱水桶
利用离心运动把附着在衣服上的水分甩掉的装置
解释:
当脱水桶转得比较慢时,水滴跟衣服的附着力F足以提供所需的向心力,使水滴做圆周运动。当桶转得比较快时,附着力 F 不足以提供所需的向心力,于是水滴做离心运动,穿过桶孔,飞到外面。
2、用离心机把体温计的水银柱甩回玻璃泡内
当离心机转得比较慢时,缩口的阻力 F 足以提供所需的向心力,缩口上方的水银柱做圆周运动。当离心机转得相当快时,阻力 F 不足以提供所需的向心力,水银柱做离心运动而进入玻璃泡内。
3、制作“棉花”糖的原理:
内筒与洗衣机的脱水筒相似,里面加入白砂糖,加热使糖熔化成糖汁。内筒高速旋转,黏稠的糖汁就做离心运动,从内筒壁的小孔飞散出去,成为丝状到达温度较低的外筒,并迅速冷却凝固,变得纤细雪白,像一团团棉花。
4、离心分离器的原理:
可以将固体和液体分离开来。
质量大的固体需要的向心力比液体大,“远离圆心的程度”比液体明显。
三、离心运动 的危害
汽车转弯为什么会翻车?
竖直平面内的圆周运动
研究与讨论
2、有无可能做这样的运动?若可能应满足怎样的条件?
G
FN
问题1:绳球模型
用长为L的细绳拴着质量为m的小球,使小球在竖直平面内做圆周运动,如图所示。
o
A
L
v1
B
v2
试分析:
(1)当小球在最低点A的速度为v1时,其绳的张力为多大?
(2)当小球在最高点B的速度为v2 时,其绳的张力与速度的关系怎样?
v1
o
mg
F2
mg
F1
思考:过最高点的最小速度是多大
(1)当F=0时,速度v为最小值
最低点:
最高点:
v2
拓展:物体沿竖直内轨运动
有一个竖直放置的内壁光滑圆环,其半径为R,质量为m的小球沿它的内表面做圆周运动,分析小球在最高点A的速度应满足什么条件?
v
A
mg
FN
A
明确:向心力和向心加速度公式同样适合于变速圆周运动,但求质点在圆周上某点的向心力和向心加速度的大小,必须用该点的瞬时速度值。
小结:
实例一:水流星
思考: 在“水流星”的表演中,杯子在竖直面内做圆周运动,到最高点时,杯口朝下,但杯中的水却不会流下来,为什么呢?
作圆周运动的物体总需要向心力。当杯子以速度v 转过最高点时,杯中的水受力如图所示。
对杯中的水:
G
FN
由此可知,v 越大,杯子底对水的压力越大。
FN = 0
此时水恰好不流出。
表演“水流星”节目的演员,需要保证杯子在圆周运动最高点的线速度不得小于
即∶
思考:过山车为什么在最高点也不会掉下来?
实例二:过山车
G
FN
FN = 0
要想保证过山车在最高点不掉下来,此时速度
问题2:杆物模型:
用长为L的轻杆一端固定着一个质量为m的小球,使小球在竖直平面内做圆周运动,如图所示。
试分析:
(1)当小球在最低点A的速度为v2时,杆的受力与速度的关系怎样?
(2)当小球在最高点B的速度为v1时,杆的受力与速度的关系怎样?
A
B
F3
mg
F1
mg
F2
v1
v2
o
思考:过最高点的最小速度是多大 何时杆子表现为拉力,何时表现为支持力
问题2:杆物模型:
A
B
拓展:物体在管型轨道内的运动
如图,有一内壁光滑竖直放置的管型轨道半径为R,内有一质量为m的小球,沿其竖直方向上的做变速圆周运动,小球的直径刚好与管的内径相等
(1)小球在运动到最高点的时候速度与受力的关系是怎样的?
(2)小球运动到最低点的时候速度与受力的关系又是怎样?
G
V1(V2)
A
G
F3
V3
分析:
F1
F2
R
最高点:
;
最低点:
思考:小球在最高点的最小速度可以是多少?什么时候外管壁对小球有压力,什么时候内管壁对小球有支持力 什么时候内外管壁都没有压力?
(1)最高点最小速度
(2)当
时,管壁对小球没有力的作用
时,外管壁对小球有作用力
(3)当
V >
时,内管壁对小球有作用力
(4)当
V <
长为0.6 m的轻杆OA(不计质量), A端插个质量为2.0 kg的物体,在竖直平面内绕O点做圆周运动,当球达到最高点的速度分别为3 m/s, m/s, 2 m/s时, 求杆对球的作用力各为多少
O
A
巩固应用:
