人教版七年级数学上册第2章 整式的加减 章末复习达标测试卷(一)(含答案)
文档属性
| 名称 | 人教版七年级数学上册第2章 整式的加减 章末复习达标测试卷(一)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 112.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-22 21:57:50 | ||
图片预览

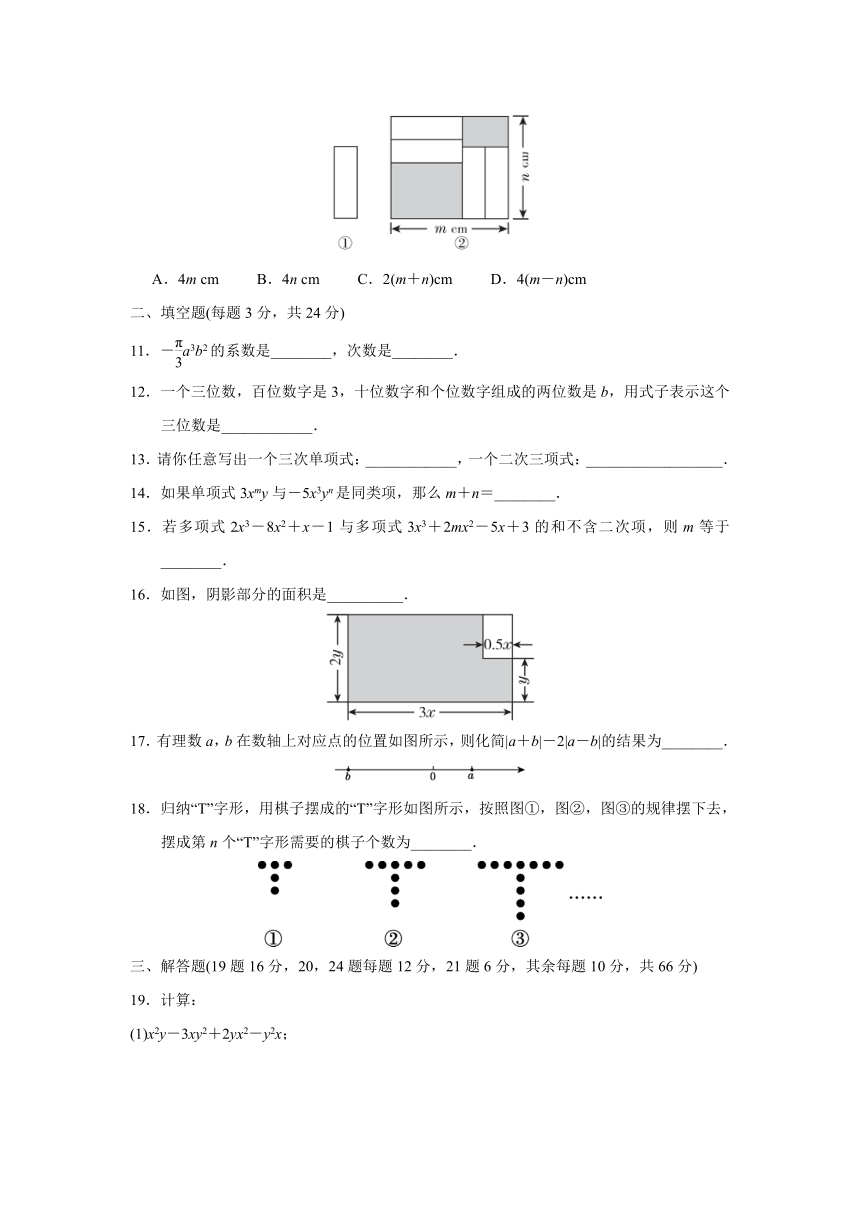

文档简介
第二章达标测试卷
一、选择题(每题3分,共30分)
1.下列各式中,是单项式的是( )
A.x2-1 B.a2b C. D.
2.多项式-5--y中,二次项的系数是( )
A.2 B.-2 C.- D.
3.下列各组单项式中,是同类项的是( )
A.与a2b B.3x2y与3xy2 C.a与1 D.2bc与2abc
4.下列运算正确的是( )
A.3a+6b=9ab B.3a2b-3ba2=0 C.8a4-6a3=2a D.y2-y2=
5.某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是( )
A.(a-10%)(a+15%)万元 B.a(1-10%)(1+15%)万元
C.(a-10%+15%)万元 D.a(1-10%+15%)万元
6.下列各式去括号正确的是( )
A.x2-(x-y+2z)=x2-x+y+2z B.x-(-2x+3y-1)=x+2x-3y+1
C.3x-[5x-(x-1)]=3x-5x-x+1 D.(x-1)-(x2-2)=x-1-x2-2
7.已知a-b=1,则式子-3a+3b-11的值是( )
A.-14 B.1 C.-8 D.5
8.x2+ax-2y+7-(bx2-2x+9y-1)的值与x的取值无关,则a+b的值为( )
A.-1 B.1 C.-2 D.2
9.某同学计算一个多项式加上xy-3yz-2xz时,误认为减去此式,计算出的结果为xy-2yz+3xz,则正确结果是( )
A.2xy-5yz+xz B.3xy-8yz-xz C.yz+5xz D.3xy-8yz+xz
10.把四张形状、大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
A.4m cm B.4n cm C.2(m+n)cm D.4(m-n)cm
二、填空题(每题3分,共24分)
11.-a3b2的系数是________,次数是________.
12.一个三位数,百位数字是3,十位数字和个位数字组成的两位数是b,用式子表示这个三位数是____________.
13.请你任意写出一个三次单项式:____________,一个二次三项式:__________________.
14.如果单项式3xmy与-5x3yn是同类项,那么m+n=________.
15.若多项式2x3-8x2+x-1与多项式3x3+2mx2-5x+3的和不含二次项,则m等于________.
16.如图,阴影部分的面积是__________.
17.有理数a,b在数轴上对应点的位置如图所示,则化简|a+b|-2|a-b|的结果为________.
18.归纳“T”字形,用棋子摆成的“T”字形如图所示,按照图①,图②,图③的规律摆下去,摆成第n个“T”字形需要的棋子个数为________.
三、解答题(19题16分,20,24题每题12分,21题6分,其余每题10分,共66分)
19.计算:
(1)x2y-3xy2+2yx2-y2x;
(2)a2b-0.4ab2-a2b+ab2;
(3)2(x2-2x+5)-3(2x2-5);
(4)5(a2b-3ab2)-2(a2b-7ab2).
20.先化简,再求值:
(1)(4a+3a2-3+3a3)-(-a+4a3),其中a=-2;
(2)(2x2y-2xy2)-,其中x=-1,y=2.
21.若多项式3x3-2x2+3x-1与多项式x2-2mx3+2x+3的和为二次三项式,求m的值.
22.按如图所示的程序计算.
(1)填写表内空格:
输入n 3 2 -2 …
输出答案 …
(2)你发现的规律是__________________________;
(3)用简要过程说明你发现的规律的正确性.
23.先阅读下面的文字,然后按要求解题.
例:1+2+3+…+100=?
如果一个一个顺次相加显然太烦琐,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算、提高计算速度的.
因为1+100=2+99=3+98=…=50+51=101,
所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=101×________=________.
(1)补全例题的解题过程;
(2)计算:a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
24.为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段以达到节水的目的.该市自来水收费价格见如图所示的价目表.
(1)若某户居民2月份用水4 m3,则应交水费________元;
(2)若某户居民3月份用水a m3(其中6(3)若某户居民4,5月份共用水15 m3(5月份用水量超过了4月份),设4月份用水x m3,求该户居民4,5月份共交水费多少元.(用含x的整式表示并化简)
答案
一、1.B 2.C 3.A 4.B 5.B 6.B 7.A 8.A 9.B
10.B 点拨:设小长方形卡片的长为x cm,宽为y cm,则x+2y=m,故两块阴影部分的周长和为2(n-x)+2(n-2y)+2m=4n-2(x+2y)+2m=4n(cm).
二、11.-;5 12. 300+b
13.x2y;x2-x+1(答案不唯一)
14.4 15.4 16.xy 17.-3a+b
18.3n+2
三、19.解:(1)原式=3x2y-4xy2;
(2)原式=-a2b;
(3)原式=2x2-4x+10-6x2+15=-4x2-4x+25;
(4)原式=5a2b-15ab2-2a2b+14ab2=3a2b-ab2.
20.解:(1)原式=4a+3a2-3+3a3+a-4a3=-a3+3a2+5a-3.
当a=-2时,原式=-(-2)3+3×(-2)2+5×(-2)-3=-(-8)+3×4+5×(-2)-3=8+12-10-3=7.
(2)原式=2x2y-2xy2+3x2y2-3x2y-3x2y2+3xy2=-x2y+xy2.
当x=-1,y=2时,原式=-(-1)2×2+(-1)×22=-1×2+(-1)×4=-2-4=-6.
21.解:(3x3-2x2+3x-1)+(x2-2mx3+2x+3)=(3-2m)x3-x2+5x+2.
依题意得3-2m=0,故m=.
22.解: (1)-1;-1;-1;-1
(2)输出答案均为-1
(3)2(n2-n)-2n2+2n-1=2n2-2n-2n2+2n-1=-1,即输出答案与n的值无关,均为-1.
23.解:(1)50;5 050
(2)原式=+[(b+99b)+(2b+98b)+…+(49b+51b)+50b]=100a+(49×100b+50b)=100a+4 950b.
24.解:(1)8
(2)4(a-6)+6×2=4a-12(元),即应交水费(4a-12)元.
(3)因为5月份用水量超过了4月份,所以4月份用水量少于7.5 m3.
当4月份用水量少于5 m3时,5月份用水量超出10 m3,
故4,5月份共交水费2x+8(15-x-10)+4×4+6×2=-6x+68(元);
当4月份用水量不低于5 m3但不超出6 m3时,5月份用水量不少于9 m3但不超出10 m3,
故4,5月份共交水费2x+4(15-x-6)+ 6×2=-2x+48(元);
当4月份用水量超出6 m3但少于7.5 m3时,5月份用水量超出7.5 m3但少于9 m3,
故4,5月份共交水费4(x-6)+ 6×2+4(15-x-6) + 6×2=36(元).
一、选择题(每题3分,共30分)
1.下列各式中,是单项式的是( )
A.x2-1 B.a2b C. D.
2.多项式-5--y中,二次项的系数是( )
A.2 B.-2 C.- D.
3.下列各组单项式中,是同类项的是( )
A.与a2b B.3x2y与3xy2 C.a与1 D.2bc与2abc
4.下列运算正确的是( )
A.3a+6b=9ab B.3a2b-3ba2=0 C.8a4-6a3=2a D.y2-y2=
5.某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是( )
A.(a-10%)(a+15%)万元 B.a(1-10%)(1+15%)万元
C.(a-10%+15%)万元 D.a(1-10%+15%)万元
6.下列各式去括号正确的是( )
A.x2-(x-y+2z)=x2-x+y+2z B.x-(-2x+3y-1)=x+2x-3y+1
C.3x-[5x-(x-1)]=3x-5x-x+1 D.(x-1)-(x2-2)=x-1-x2-2
7.已知a-b=1,则式子-3a+3b-11的值是( )
A.-14 B.1 C.-8 D.5
8.x2+ax-2y+7-(bx2-2x+9y-1)的值与x的取值无关,则a+b的值为( )
A.-1 B.1 C.-2 D.2
9.某同学计算一个多项式加上xy-3yz-2xz时,误认为减去此式,计算出的结果为xy-2yz+3xz,则正确结果是( )
A.2xy-5yz+xz B.3xy-8yz-xz C.yz+5xz D.3xy-8yz+xz
10.把四张形状、大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
A.4m cm B.4n cm C.2(m+n)cm D.4(m-n)cm
二、填空题(每题3分,共24分)
11.-a3b2的系数是________,次数是________.
12.一个三位数,百位数字是3,十位数字和个位数字组成的两位数是b,用式子表示这个三位数是____________.
13.请你任意写出一个三次单项式:____________,一个二次三项式:__________________.
14.如果单项式3xmy与-5x3yn是同类项,那么m+n=________.
15.若多项式2x3-8x2+x-1与多项式3x3+2mx2-5x+3的和不含二次项,则m等于________.
16.如图,阴影部分的面积是__________.
17.有理数a,b在数轴上对应点的位置如图所示,则化简|a+b|-2|a-b|的结果为________.
18.归纳“T”字形,用棋子摆成的“T”字形如图所示,按照图①,图②,图③的规律摆下去,摆成第n个“T”字形需要的棋子个数为________.
三、解答题(19题16分,20,24题每题12分,21题6分,其余每题10分,共66分)
19.计算:
(1)x2y-3xy2+2yx2-y2x;
(2)a2b-0.4ab2-a2b+ab2;
(3)2(x2-2x+5)-3(2x2-5);
(4)5(a2b-3ab2)-2(a2b-7ab2).
20.先化简,再求值:
(1)(4a+3a2-3+3a3)-(-a+4a3),其中a=-2;
(2)(2x2y-2xy2)-,其中x=-1,y=2.
21.若多项式3x3-2x2+3x-1与多项式x2-2mx3+2x+3的和为二次三项式,求m的值.
22.按如图所示的程序计算.
(1)填写表内空格:
输入n 3 2 -2 …
输出答案 …
(2)你发现的规律是__________________________;
(3)用简要过程说明你发现的规律的正确性.
23.先阅读下面的文字,然后按要求解题.
例:1+2+3+…+100=?
如果一个一个顺次相加显然太烦琐,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算、提高计算速度的.
因为1+100=2+99=3+98=…=50+51=101,
所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=101×________=________.
(1)补全例题的解题过程;
(2)计算:a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
24.为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段以达到节水的目的.该市自来水收费价格见如图所示的价目表.
(1)若某户居民2月份用水4 m3,则应交水费________元;
(2)若某户居民3月份用水a m3(其中6
答案
一、1.B 2.C 3.A 4.B 5.B 6.B 7.A 8.A 9.B
10.B 点拨:设小长方形卡片的长为x cm,宽为y cm,则x+2y=m,故两块阴影部分的周长和为2(n-x)+2(n-2y)+2m=4n-2(x+2y)+2m=4n(cm).
二、11.-;5 12. 300+b
13.x2y;x2-x+1(答案不唯一)
14.4 15.4 16.xy 17.-3a+b
18.3n+2
三、19.解:(1)原式=3x2y-4xy2;
(2)原式=-a2b;
(3)原式=2x2-4x+10-6x2+15=-4x2-4x+25;
(4)原式=5a2b-15ab2-2a2b+14ab2=3a2b-ab2.
20.解:(1)原式=4a+3a2-3+3a3+a-4a3=-a3+3a2+5a-3.
当a=-2时,原式=-(-2)3+3×(-2)2+5×(-2)-3=-(-8)+3×4+5×(-2)-3=8+12-10-3=7.
(2)原式=2x2y-2xy2+3x2y2-3x2y-3x2y2+3xy2=-x2y+xy2.
当x=-1,y=2时,原式=-(-1)2×2+(-1)×22=-1×2+(-1)×4=-2-4=-6.
21.解:(3x3-2x2+3x-1)+(x2-2mx3+2x+3)=(3-2m)x3-x2+5x+2.
依题意得3-2m=0,故m=.
22.解: (1)-1;-1;-1;-1
(2)输出答案均为-1
(3)2(n2-n)-2n2+2n-1=2n2-2n-2n2+2n-1=-1,即输出答案与n的值无关,均为-1.
23.解:(1)50;5 050
(2)原式=+[(b+99b)+(2b+98b)+…+(49b+51b)+50b]=100a+(49×100b+50b)=100a+4 950b.
24.解:(1)8
(2)4(a-6)+6×2=4a-12(元),即应交水费(4a-12)元.
(3)因为5月份用水量超过了4月份,所以4月份用水量少于7.5 m3.
当4月份用水量少于5 m3时,5月份用水量超出10 m3,
故4,5月份共交水费2x+8(15-x-10)+4×4+6×2=-6x+68(元);
当4月份用水量不低于5 m3但不超出6 m3时,5月份用水量不少于9 m3但不超出10 m3,
故4,5月份共交水费2x+4(15-x-6)+ 6×2=-2x+48(元);
当4月份用水量超出6 m3但少于7.5 m3时,5月份用水量超出7.5 m3但少于9 m3,
故4,5月份共交水费4(x-6)+ 6×2+4(15-x-6) + 6×2=36(元).
