苏教版(2019)高中数学必修第二册 14.3统计图表教学设计
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 14.3统计图表教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 779.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 11:42:04 | ||
图片预览



文档简介
第十四章 统计
14.3 统计图表
教材从设计上要求学生体会不同抽样方法的特点,鼓励学生从统计图表和基本数字特征中获取尽可能多的有用信息,体会统计图表和基本数字特征的特点;鼓励学生根据样本的信息对总体作出推断,体会用样本估计总体的思想,认识统计的作用和统计思维的特征;鼓励学生对数据处理过程进行反思,形成对数据处理过程进行初步评价的意识;鼓励学生通过不同视角或方法进行统计分析,在比较中深化认识统计量,提高统计分析的能力;
课程目标 学科素养
1.掌握频率分布表的作法以及频率直方图的画法. 2.掌握用频率直方图估计总体. 在学习绘制频率分布直方图的过程中,掌握应用频率分布直方图等统计图表估计总体的取值规律,发展学生数据分析的素养.
1.教学重点:掌握频率分布表的作法以及频率直方图的画法.
2.教学难点:掌握用频率直方图估计总体.
多媒体调试、讲义分发。
下面按时间顺序(从1789年的华盛顿到2017年的特朗普,共45任)给出了历届美国总统就任时的年龄:57,61,57,57,58,57,61,54,68,51,49,64,50,48,65,52,56,46,54,49,51,47,55,55,54,42,51,56,55,51,54,51,60,62,43,55,56,61,52,69,64,46,54,48,70.
问题 你能很容易地看出这些数据有什么规律吗?若不能,对这些数据如何处理才可以?
提示 不能.应对这些数据进行整理,用统计图表表示出来才容易看出其规律.
知识点一 扇形统计图、折线统计图、频数直方图
统计图表 主要应用
扇形统计图 直观描述各类数据占总数的比例
频数直方图 反映分布状况,又可以表示变化趋势
折线统计图 描述数据随时间的变化趋势
知识点二 频率分布表
一般地,制作频率分布表的步骤如下
(1)求全距,决定组数和组距,组距=.
(2)分组,通常对组内数值所在区间取左闭右开区间,最后一组取闭区间.
(3)登记频数,计算频率,列出频率分布表.
知识点三 频率直方图与折线图
1.频率直方图
在频率直方图中,纵轴表示,数据落在各小组内的频率用小长方形的面积来表示,各小长方形的面积的总和等于1.
2.频率折线图
将频率直方图中各个矩形的上底边的中点顺次连接起来,并将两边端点向外延伸半个组距,就得到频率折线图,简称折线图.
一、折线图、条形图、扇形图及应用
例1 如图是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,试根据折线统计图反映的信息,绘制该市3月1日到10日最低气温(单位:℃)的扇形统计图和频数直方图.
解 该城市3月1日至10日的最低气温(单位:℃)情况如下表:
日期 1 2 3 4 5 6 7 8 9 10
最低气温(℃) -3 -2 0 -1 1 2 0 -1 2 2
其中最低气温为-3 ℃的有1天,占10%,最低气温为-2 ℃的有1天,占10%,最低气温为-1 ℃的有2天,占20%,最低气温为0 ℃的有2天,占20%,最低气温为1 ℃的有1天,占10%,最低气温为2 ℃的有3天,占30%,扇形统计图如图所示.
频数直方图如图所示.
反思感悟 (1)频数直方图是用一个单位长度表示一定的数量或频率,根据数量的多少或频率的大小画成长短不同的矩形条,条形图能清楚地表示出每个项目的具体数目或频率.
(2)扇形图是用整个圆面积表示总数(100%),用圆内的扇形面积表示各个部分所占总数的百分数.
(3)在画折线图时,要注意明确横轴、纵轴的实际含义.
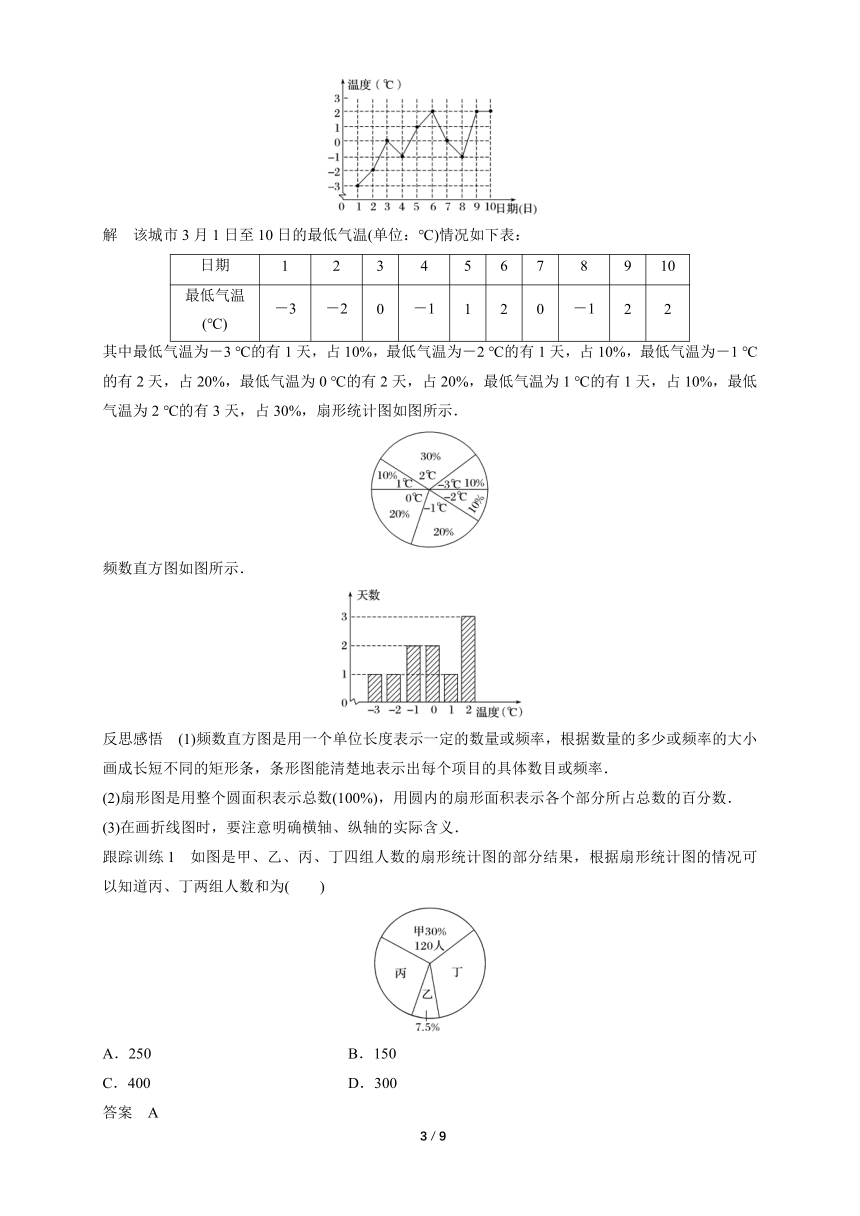
跟踪训练1 如图是甲、乙、丙、丁四组人数的扇形统计图的部分结果,根据扇形统计图的情况可以知道丙、丁两组人数和为( )
A.250 B.150
C.400 D.300
答案 A
解析 甲组人数是120,占30%,则总人数是=400.则乙组人数是400×7.5%=30,则丙、丁两组人数和为400-120-30=250.
二、画频率直方图
例2 从某校高三学生中抽取50名参加数学竞赛,成绩分组(单位:分)及各组的频数如下:
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表(含累积频率);
(2)画出频率直方图;
(3)估计成绩在[60,90)分的学生比例.
解 (1)频率分布表如下.
成绩分组 频数 频率
[40,50) 2 0.04 0.004
[50,60) 3 0.06 0.006
[60,70) 10 0.2 0.02
[70,80) 15 0.3 0.03
[80,90) 12 0.24 0.024
[90,100] 8 0.16 0.016
合计 50 1.00 0.1
(2)频率直方图如图所示.
(3)学生成绩在[60,90)分的频率为0.2+0.3+0.24=0.74=74%,所以估计成绩在[60,90)分的学生比例为74%.
反思感悟 绘制频率直方图的注意点
(1)各组频率的和等于1,因此,各小矩形的面积之和也等于1.
(2)在xOy坐标平面内画频率直方图时,x=样本数据,y=,这样每一组的频率可以用该组的组距为底、为高的小矩形的面积来表示.其中,矩形的高==×频数.
(3)同样一组数据,如果组距不同,横轴、纵轴单位不同,得到的频率直方图的形状也会不同.
跟踪训练2 一个农技站为了考察某种大麦穗生长的分布情况,在一块试验田里抽取了100株麦穗,量得长度如下(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.6 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
根据上面的数据列出频率分布表,绘制出频率直方图,并估计在这块试验田里长度在5.75~6.35 cm之间的麦穗所占的百分比.
解 (1)由题中数据可知,这组数据的最大值为7.4,最小值为4.0,故全距为3.4.
(2)决定组距与组数:若取组距为0.3,因为≈11.3,需分为12组,组数合适,所以取组距为0.3,组数为12.
(3)分组所分的12个小组可以是3.95~4.25,4.25~4.55,4.55~4.85,…,7.25~7.55.
(4)列频率分布表:
分组 频数 频率
[3.95,4.25) 1 0.01
[4.25,4.55) 1 0.01
[4.55,4.85) 2 0.02
[4.85,5.15) 5 0.05
[5.15,5.45) 11 0.11
[5.45,5.75) 15 0.15
[5.75,6.05) 28 0.28
[6.05,6.35) 13 0.13
[6.35,6.65) 11 0.11
[6.65,6.95) 10 0.10
[6.95,7.25) 2 0.02
[7.25,7.55] 1 0.01
合计 100 1.00
(5)绘制频率直方图如图.
从表中看到,样本数据落在5.75~6.35之间的频率是0.28+0.13=0.41,于是可以估计,在这块试验田里长度在5.75~6.35 cm之间的麦穗约占41%.
三、频率直方图的应用
例3 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率直方图:
组号 分组 频数
1 [0,2) 6
2 [2,4) 8
3 [4,6) 17
4 [6,8) 22
5 [8,10) 25
6 [10,12) 12
7 [12,14) 6
8 [14,16) 2
9 [16,18] 2
合计 100
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的频率;
(2)求频率直方图中的a,b的值.
解 (1)根据频数分布表知,100名学生中一周课外阅读时间不少于12小时的学生共有6+2+2=10(名),
所以样本中的学生一周课外阅读时间少于12小时的频率是1-=0.9.
(2)课外阅读时间落在[4,6)组内的有17人,频率为0.17,所以a===0.085.课外阅读时间落在[8,10)组内的有25人,频率为0.25,
所以b===0.125.
反思感悟 频率直方图的性质
(1)因为小矩形的面积=组距×=频率,所以各小矩形的面积表示相应各组的频率.这样,频率直方图就以面积的形式反映了数据落在各个小组内的频率大小.
(2)在频率直方图中,各小矩形的面积之和等于1.
(3)=样本容量.
跟踪训练3 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率直方图如图所示.
(1)求频率直方图中x的值;
(2)在这些用户中,求用电量落在区间[100,250)内的户数.
解 (1)由频率直方图知[200,250)小组的频率为1-(0.002 4+0.003 6+0.006 0+0.002 4+0.001 2)×50=0.22,于是x==0.004 4.
(2)∵数据落在[100,250)内的频率为(0.003 6+0.006 0+0.004 4)×50=0.7,
∴所求户数为0.7×100=70.
1.如图是某手机商城中A,B,C三种品牌的手机各季度销量的百分比条形图,根据该图,以下结论中一定正确的是( )
A.四个季度中,每季度B品牌和C品牌总销量之和均不低于A品牌的销量
B.B品牌第二季度的销量小于第三季度的销量
C.第一季度销量最大的为C品牌,销量最小的为B品牌
D.A品牌的全年销量最大
答案 D
解析 对于A,第四季度中,A品牌销量大于50%,B品牌和C品牌总销量之和小于50%,故A错误;对于B,因为B品牌每个季度的销量不确定,所以无法判断,故B错误;对于C,第一季度销量最大的是A品牌,故C错误;对于D,由题图知,四个季度A品牌的销量都最大,所以A品牌的全年销量最大,D正确.
2.观察新生儿的体重,其频率直方图如图所示,则新生儿体重在[2 700,3 000)内的频率为( )
A.0.1 B.0.2
C.0.3 D.0.4
答案 C
解析 由题图可得,新生儿体重在[2 700,3 000)内的频率为0.001×300=0.3.
3.一个容量为20的样本数据,分组与频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则样本在[10,50)内的频率为( )
A.0.5 B.0.24 C.0.6 D.0.7
答案 D
解析 因为样本在[10,50)内的频数为2+3+4+5=14,样本容量为20,所以在[10,50)内的频率为=0.7.
4.(多选)容量为100的样本,其数据分布在[2,18]内,将样本数据分为4组:[2,6),[6,10),[10,14),[14,18],得到频率直方图如图所示,则下列说法中正确的是( )
A.样本数据分布在[6,10)内的频率为0.32
B.样本数据分布在[10,14)内的频数为40
C.样本数据分布在[2,10)内的频数为40
D.估计总体数据大约有10%分布在[10,14)内
答案 ABC
解析 对于A,由题图可得,样本数据分布在[6,10)内的频率为0.08×4=0.32,所以A正确.对于B,由题图可得,样本数据分布在[10,14)内的频数为100×(0.1×4)=40,所以B正确.对于C,由题图可得,样本数据分布在[2,10)内的频数为100×(0.02+0.08)×4=40,所以C正确.对于D,由题图可估计,总体数据分布在[10,14)内的比例为0.1×4=0.4=40%,所以D错误,故选ABC.
5.为了解今年某校高三毕业班准备报考飞行员学生的体重(单位:千克)情况,将所得的数据整理后,画出了频率直方图,如图所示,已知图中从左到右的前三个小组的频率之比为1∶2∶3,其中第2小组的频数为12.则该校报考飞行员的总人数为________.
答案 48
解析 设报考飞行员的总人数为n,
设第1小组的频率为a,则有a+2a+3a+(0.013+0.037)×5=1,解得a=0.125,
所以第2小组的频率为0.25.
又第2小组的频数为12,则有0.25=,所以n=48.
由于总体取值不易知道,因此我们用样本取值的规律去估计总体取值的规律,并且常借助于如下统计图表:频率分布直方图、条形图、折线图、扇形图等.
2 / 9
14.3 统计图表
教材从设计上要求学生体会不同抽样方法的特点,鼓励学生从统计图表和基本数字特征中获取尽可能多的有用信息,体会统计图表和基本数字特征的特点;鼓励学生根据样本的信息对总体作出推断,体会用样本估计总体的思想,认识统计的作用和统计思维的特征;鼓励学生对数据处理过程进行反思,形成对数据处理过程进行初步评价的意识;鼓励学生通过不同视角或方法进行统计分析,在比较中深化认识统计量,提高统计分析的能力;
课程目标 学科素养
1.掌握频率分布表的作法以及频率直方图的画法. 2.掌握用频率直方图估计总体. 在学习绘制频率分布直方图的过程中,掌握应用频率分布直方图等统计图表估计总体的取值规律,发展学生数据分析的素养.
1.教学重点:掌握频率分布表的作法以及频率直方图的画法.
2.教学难点:掌握用频率直方图估计总体.
多媒体调试、讲义分发。
下面按时间顺序(从1789年的华盛顿到2017年的特朗普,共45任)给出了历届美国总统就任时的年龄:57,61,57,57,58,57,61,54,68,51,49,64,50,48,65,52,56,46,54,49,51,47,55,55,54,42,51,56,55,51,54,51,60,62,43,55,56,61,52,69,64,46,54,48,70.
问题 你能很容易地看出这些数据有什么规律吗?若不能,对这些数据如何处理才可以?
提示 不能.应对这些数据进行整理,用统计图表表示出来才容易看出其规律.
知识点一 扇形统计图、折线统计图、频数直方图
统计图表 主要应用
扇形统计图 直观描述各类数据占总数的比例
频数直方图 反映分布状况,又可以表示变化趋势
折线统计图 描述数据随时间的变化趋势
知识点二 频率分布表
一般地,制作频率分布表的步骤如下
(1)求全距,决定组数和组距,组距=.
(2)分组,通常对组内数值所在区间取左闭右开区间,最后一组取闭区间.
(3)登记频数,计算频率,列出频率分布表.
知识点三 频率直方图与折线图
1.频率直方图
在频率直方图中,纵轴表示,数据落在各小组内的频率用小长方形的面积来表示,各小长方形的面积的总和等于1.
2.频率折线图
将频率直方图中各个矩形的上底边的中点顺次连接起来,并将两边端点向外延伸半个组距,就得到频率折线图,简称折线图.
一、折线图、条形图、扇形图及应用
例1 如图是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,试根据折线统计图反映的信息,绘制该市3月1日到10日最低气温(单位:℃)的扇形统计图和频数直方图.
解 该城市3月1日至10日的最低气温(单位:℃)情况如下表:
日期 1 2 3 4 5 6 7 8 9 10
最低气温(℃) -3 -2 0 -1 1 2 0 -1 2 2
其中最低气温为-3 ℃的有1天,占10%,最低气温为-2 ℃的有1天,占10%,最低气温为-1 ℃的有2天,占20%,最低气温为0 ℃的有2天,占20%,最低气温为1 ℃的有1天,占10%,最低气温为2 ℃的有3天,占30%,扇形统计图如图所示.
频数直方图如图所示.
反思感悟 (1)频数直方图是用一个单位长度表示一定的数量或频率,根据数量的多少或频率的大小画成长短不同的矩形条,条形图能清楚地表示出每个项目的具体数目或频率.
(2)扇形图是用整个圆面积表示总数(100%),用圆内的扇形面积表示各个部分所占总数的百分数.
(3)在画折线图时,要注意明确横轴、纵轴的实际含义.
跟踪训练1 如图是甲、乙、丙、丁四组人数的扇形统计图的部分结果,根据扇形统计图的情况可以知道丙、丁两组人数和为( )
A.250 B.150
C.400 D.300
答案 A
解析 甲组人数是120,占30%,则总人数是=400.则乙组人数是400×7.5%=30,则丙、丁两组人数和为400-120-30=250.
二、画频率直方图
例2 从某校高三学生中抽取50名参加数学竞赛,成绩分组(单位:分)及各组的频数如下:
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表(含累积频率);
(2)画出频率直方图;
(3)估计成绩在[60,90)分的学生比例.
解 (1)频率分布表如下.
成绩分组 频数 频率
[40,50) 2 0.04 0.004
[50,60) 3 0.06 0.006
[60,70) 10 0.2 0.02
[70,80) 15 0.3 0.03
[80,90) 12 0.24 0.024
[90,100] 8 0.16 0.016
合计 50 1.00 0.1
(2)频率直方图如图所示.
(3)学生成绩在[60,90)分的频率为0.2+0.3+0.24=0.74=74%,所以估计成绩在[60,90)分的学生比例为74%.
反思感悟 绘制频率直方图的注意点
(1)各组频率的和等于1,因此,各小矩形的面积之和也等于1.
(2)在xOy坐标平面内画频率直方图时,x=样本数据,y=,这样每一组的频率可以用该组的组距为底、为高的小矩形的面积来表示.其中,矩形的高==×频数.
(3)同样一组数据,如果组距不同,横轴、纵轴单位不同,得到的频率直方图的形状也会不同.
跟踪训练2 一个农技站为了考察某种大麦穗生长的分布情况,在一块试验田里抽取了100株麦穗,量得长度如下(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.6 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
根据上面的数据列出频率分布表,绘制出频率直方图,并估计在这块试验田里长度在5.75~6.35 cm之间的麦穗所占的百分比.
解 (1)由题中数据可知,这组数据的最大值为7.4,最小值为4.0,故全距为3.4.
(2)决定组距与组数:若取组距为0.3,因为≈11.3,需分为12组,组数合适,所以取组距为0.3,组数为12.
(3)分组所分的12个小组可以是3.95~4.25,4.25~4.55,4.55~4.85,…,7.25~7.55.
(4)列频率分布表:
分组 频数 频率
[3.95,4.25) 1 0.01
[4.25,4.55) 1 0.01
[4.55,4.85) 2 0.02
[4.85,5.15) 5 0.05
[5.15,5.45) 11 0.11
[5.45,5.75) 15 0.15
[5.75,6.05) 28 0.28
[6.05,6.35) 13 0.13
[6.35,6.65) 11 0.11
[6.65,6.95) 10 0.10
[6.95,7.25) 2 0.02
[7.25,7.55] 1 0.01
合计 100 1.00
(5)绘制频率直方图如图.
从表中看到,样本数据落在5.75~6.35之间的频率是0.28+0.13=0.41,于是可以估计,在这块试验田里长度在5.75~6.35 cm之间的麦穗约占41%.
三、频率直方图的应用
例3 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率直方图:
组号 分组 频数
1 [0,2) 6
2 [2,4) 8
3 [4,6) 17
4 [6,8) 22
5 [8,10) 25
6 [10,12) 12
7 [12,14) 6
8 [14,16) 2
9 [16,18] 2
合计 100
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的频率;
(2)求频率直方图中的a,b的值.
解 (1)根据频数分布表知,100名学生中一周课外阅读时间不少于12小时的学生共有6+2+2=10(名),
所以样本中的学生一周课外阅读时间少于12小时的频率是1-=0.9.
(2)课外阅读时间落在[4,6)组内的有17人,频率为0.17,所以a===0.085.课外阅读时间落在[8,10)组内的有25人,频率为0.25,
所以b===0.125.
反思感悟 频率直方图的性质
(1)因为小矩形的面积=组距×=频率,所以各小矩形的面积表示相应各组的频率.这样,频率直方图就以面积的形式反映了数据落在各个小组内的频率大小.
(2)在频率直方图中,各小矩形的面积之和等于1.
(3)=样本容量.
跟踪训练3 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率直方图如图所示.
(1)求频率直方图中x的值;
(2)在这些用户中,求用电量落在区间[100,250)内的户数.
解 (1)由频率直方图知[200,250)小组的频率为1-(0.002 4+0.003 6+0.006 0+0.002 4+0.001 2)×50=0.22,于是x==0.004 4.
(2)∵数据落在[100,250)内的频率为(0.003 6+0.006 0+0.004 4)×50=0.7,
∴所求户数为0.7×100=70.
1.如图是某手机商城中A,B,C三种品牌的手机各季度销量的百分比条形图,根据该图,以下结论中一定正确的是( )
A.四个季度中,每季度B品牌和C品牌总销量之和均不低于A品牌的销量
B.B品牌第二季度的销量小于第三季度的销量
C.第一季度销量最大的为C品牌,销量最小的为B品牌
D.A品牌的全年销量最大
答案 D
解析 对于A,第四季度中,A品牌销量大于50%,B品牌和C品牌总销量之和小于50%,故A错误;对于B,因为B品牌每个季度的销量不确定,所以无法判断,故B错误;对于C,第一季度销量最大的是A品牌,故C错误;对于D,由题图知,四个季度A品牌的销量都最大,所以A品牌的全年销量最大,D正确.
2.观察新生儿的体重,其频率直方图如图所示,则新生儿体重在[2 700,3 000)内的频率为( )
A.0.1 B.0.2
C.0.3 D.0.4
答案 C
解析 由题图可得,新生儿体重在[2 700,3 000)内的频率为0.001×300=0.3.
3.一个容量为20的样本数据,分组与频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则样本在[10,50)内的频率为( )
A.0.5 B.0.24 C.0.6 D.0.7
答案 D
解析 因为样本在[10,50)内的频数为2+3+4+5=14,样本容量为20,所以在[10,50)内的频率为=0.7.
4.(多选)容量为100的样本,其数据分布在[2,18]内,将样本数据分为4组:[2,6),[6,10),[10,14),[14,18],得到频率直方图如图所示,则下列说法中正确的是( )
A.样本数据分布在[6,10)内的频率为0.32
B.样本数据分布在[10,14)内的频数为40
C.样本数据分布在[2,10)内的频数为40
D.估计总体数据大约有10%分布在[10,14)内
答案 ABC
解析 对于A,由题图可得,样本数据分布在[6,10)内的频率为0.08×4=0.32,所以A正确.对于B,由题图可得,样本数据分布在[10,14)内的频数为100×(0.1×4)=40,所以B正确.对于C,由题图可得,样本数据分布在[2,10)内的频数为100×(0.02+0.08)×4=40,所以C正确.对于D,由题图可估计,总体数据分布在[10,14)内的比例为0.1×4=0.4=40%,所以D错误,故选ABC.
5.为了解今年某校高三毕业班准备报考飞行员学生的体重(单位:千克)情况,将所得的数据整理后,画出了频率直方图,如图所示,已知图中从左到右的前三个小组的频率之比为1∶2∶3,其中第2小组的频数为12.则该校报考飞行员的总人数为________.
答案 48
解析 设报考飞行员的总人数为n,
设第1小组的频率为a,则有a+2a+3a+(0.013+0.037)×5=1,解得a=0.125,
所以第2小组的频率为0.25.
又第2小组的频数为12,则有0.25=,所以n=48.
由于总体取值不易知道,因此我们用样本取值的规律去估计总体取值的规律,并且常借助于如下统计图表:频率分布直方图、条形图、折线图、扇形图等.
2 / 9
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
