苏教版(2019)高中数学必修第二册 14.4.1用样本估计总体的集中趋势参数 教学设计
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 14.4.1用样本估计总体的集中趋势参数 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 456.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 12:17:44 | ||
图片预览



文档简介
第十四章 统计
14.4 用样本估计总体
14.4.1 用样本估计总体的集中趋势参数
在学习运用样本估计总体的过程中,要通过对具体数据的分析,使学生体会到由于样本数据具有随机性,样本所提供的信息在一定程度上反映了总体的有关特征,但与总体有一定的偏差.但是,如果抽样的方法比较合理,样本信息可以比较好地反映总体的信息,从而为人们合理地决策提供依据.由此使学生认识统计思维的特点和作用,体会统计思维与确定性思维的差异.
课程目标 学科素养
1.了解平均数为什么是“最理想”的近似值. 2.会计算一组数据的平均数. 3.会根据频率分布表或频率直方图估计平均数. 在学习和应用平均数、中位数和众数的过程中,要进行运算,对数据进行分析,发展学生的数学运算素养和数据分析素养.
1.教学重点:会计算一组数据的平均数.
2.教学难点:会根据频率分布表或频率直方图估计平均数.
多媒体调试、讲义分发。
现从甲、乙、丙三个厂家生产的同一种耐用家电产品中,各抽取8件产品,对其使用寿命进行跟踪调查,其结果如下:(单位:年)
甲:3,4,5,6,8,8,8,10;乙:4,6,6,6,8,9,12,13;丙:3,3,4,7,9,10,11,12.
问题 三家广告中都称其产品的使用寿命为8年,利用初中所学的知识,你能说明为什么吗?
提示 三个厂家是从不同角度进行了说明,以宣传自己的产品.其中甲:众数为8年,乙:平均数为8年,丙:中位数为8年.
知识点一 平均数
一般地,使(x-a1)2+(x-a2)2+…+(x-an)2=nx2-2(a1+a2+…+an)x+a+a+…+a最小的x=称为这n个数据a1,a2,…,an的平均数.
一般记为:=.
知识点二 平均数的估计
一般地,若取值为x1,x2,…,xn的频率分别为p1,p2,…,pn,则其平均数为=x1p1+x2p2+…+xnpn.
知识点三 众数与中位数
1.众数:一般地,将一组数据中出现次数最多的那个数据叫作该组数据的众数.
2.中位数:一般地,将一组数据按照从小到大的顺序排成一列,如果数据的个数为奇数,那么排在正中间的数据就是这组数据的中位数;如果数据的个数为偶数,那么排在正中间的两个数据的平均数即为这组数据的中位数.
一、平均数的计算
例1 (1)某班45名同学的年龄(单位:岁)如下:
14 15 14 16 15 17 16 15 16 16 15 15
17 13 14 15 16 16 15 14 15 15 14 15
16 17 16 15 15 15 16 15 13 16 15 15
17 14 15 16 16 15 14 15 15
求全班的平均年龄.
(2)从高三年级中抽出50名学生参加数学竞赛,由成绩得到如图所示的频率直方图.
试利用频率直方图估计高三年级学生的平均成绩.
解 (1)方法一 利用平均数的公式计算:
=×(14+15+…+15)=×684=15.2.
方法二 利用平均数的简化公式计算.
取a=15,将已知各数减去15,得
-1 0 -1 1 0 2 1 0 1 1 0 0 2 -2 -1 0 1 1 0 -1 0 0 -1 0 1 2 1 0 0 0 1 0 -2 1 0 0 2 -1 0 1 1 0 -1 0 0
′=×(-1+0+…+0)=×9=0.2,
=′+a=0.2+15=15.2.
方法三 利用加权平均数公式计算.
=×(13×2+14×7+15×20+16×12+17×4)
=×684=15.2.
即全班的平均年龄是15.2岁.
(2)样本平均数是频率直方图的“重心”,即所有数据的平均数,取每个小矩形底边的中点值乘以每个小矩形的面积再求和即可.
故平均成绩为
45×(0.004×10)+55×(0.006×10)+65×(0.02×10)+75×(0.03×10)+85×(0.024×10)+95×(0.016×10)=76.2(分).
反思感悟 (1)给定一组数据,要求其平均数可直接套用公式,若这组数据都在某一数据附近波动,可用平均数的简化公式计算,若这组数据某些数多次出现,可用加权平均数公式计算.
(2)在频率分布表中,平均数可用各组区间的组中值与对应频率之积进行估计.
(3)若一组数据的个数未知,但每一数据所占比例已知,可用频率平均数公式.
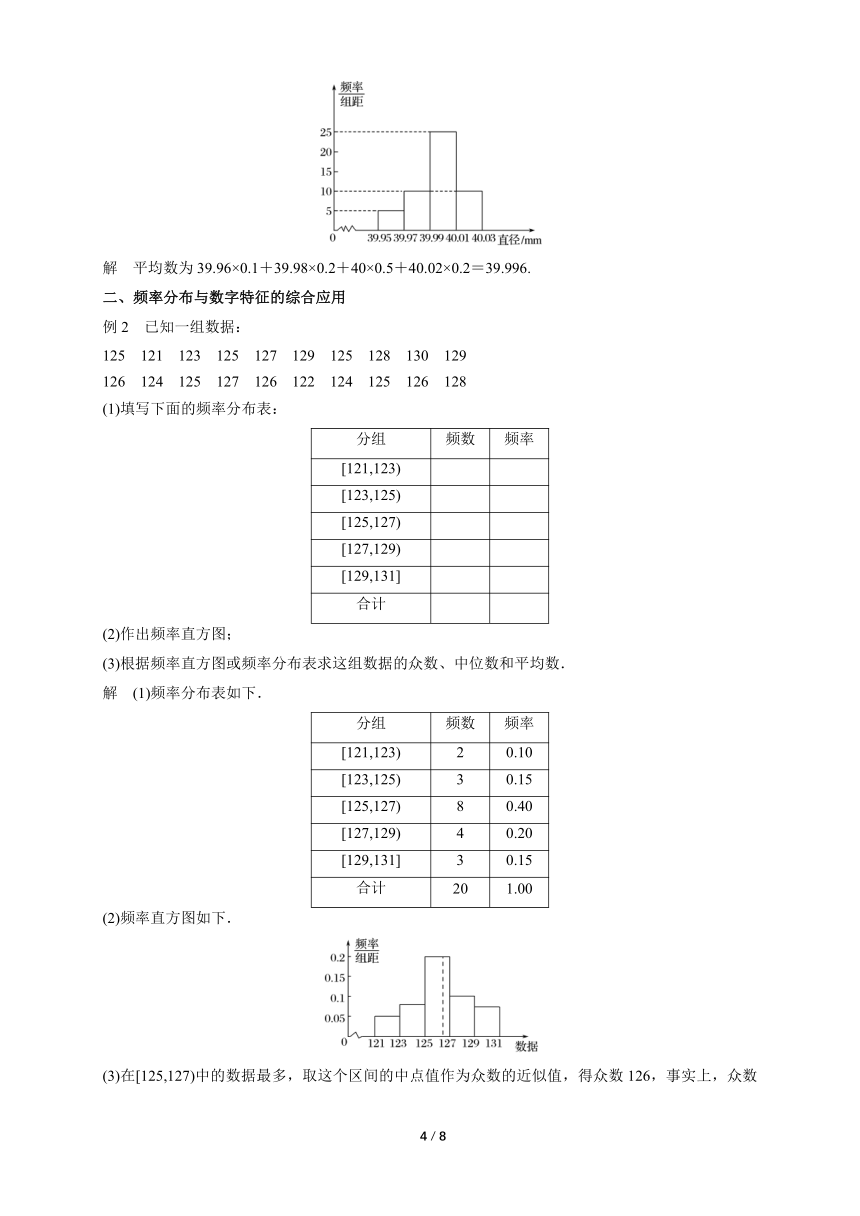
跟踪训练1 一批乒乓球,随机抽取100个进行检查,球的直径频率直方图如图.试估计这个样本的平均数.
解 平均数为39.96×0.1+39.98×0.2+40×0.5+40.02×0.2=39.996.
二、频率分布与数字特征的综合应用
例2 已知一组数据:
125 121 123 125 127 129 125 128 130 129
126 124 125 127 126 122 124 125 126 128
(1)填写下面的频率分布表:
分组 频数 频率
[121,123)
[123,125)
[125,127)
[127,129)
[129,131]
合计
(2)作出频率直方图;
(3)根据频率直方图或频率分布表求这组数据的众数、中位数和平均数.
解 (1)频率分布表如下.
分组 频数 频率
[121,123) 2 0.10
[123,125) 3 0.15
[125,127) 8 0.40
[127,129) 4 0.20
[129,131] 3 0.15
合计 20 1.00
(2)频率直方图如下.
(3)在[125,127)中的数据最多,取这个区间的中点值作为众数的近似值,得众数126,事实上,众数的精确值为125.图中虚线对应的数据是125+2×=126.25,事实上中位数为125.5.使用“组中值”求平均数:=122×0.1+124×0.15+126×0.4+128×0.2+130×0.15=126.3,
平均数的精确值为=125.75.
反思感悟 众数、中位数、平均数与频率分布表、频率直方图的关系
(1)众数:众数一般用频率表中频率最高的一小组的组中值来显示,即在样本数据的频率直方图中,最高矩形的底边中点的横坐标.
(2)中位数:在频率直方图中,中位数左边和右边的直方图的面积应该相等.
(3)平均数:平均数在频率分布表中等于组中值与对应频率之积的和.
注意 因为频率直方图不能体现样本数据,因此由频率直方图得到的中位数不一定在样本数据中出现.
跟踪训练2 在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(单位:m) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求这些运动员成绩的众数、中位数与平均数.
解 在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.题中表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70;这组数据的平均数是=(1.50×2+1.60×3+…+1.90×1)=≈1.69.
三、数字特征的应用
例3 某公司的33名职工的月工资(单位:元)如下表:
职位 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5 500 5 000 3 500 3 000 2 500 2 000 1 500
(1)求该公司职工月工资的平均数、中位数、众数;
(2)若董事长、副董事长的工资分别从5 500元、5 000元提升到30 000元、20 000元,那么公司职工的月工资的新的平均数、中位数和众数又是什么?
(3)你认为哪个统计量更能反映这个公司职工的工资水平?
解 (1)公司职工月工资的平均数为
=
=≈2 091.
若把所有数据从小到大排序,则得到中位数是1 500,众数是1 500.
(2)当董事长、副董事长的工资提升后,职工月工资的平均数为
=
=≈3 288.
中位数是1 500,众数是1 500.
(3)在这个问题中,中位数和众数都能反映出这个公司职工的工资水平,因为公司少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司职工的工资水平.
反思感悟 三种数字特征的比较
名称 优点 缺点
众数 ①体现了样本数据的最大集中点; ②容易计算 ①它只能表达样本数据中很少的一部分信息; ②无法客观地反映总体的特征
中位数 ①不受少数几个极端数据(即排序靠前或靠后的数据)的影响; ②容易计算,便于利用中间数据的信息 对极端值不敏感
平均数 代表性较好,是反映数据集中趋势的量.一般情况下,可以反映出更多的关于样本数据全体的信息 任何一个数据的改变都会引起平均数的改变.数据越“离群”,对平均数的影响越大
跟踪训练3 某地区100位居民的人均月用水量(单位:t)的分组及各组的频数如下:
[0,0.5),4;[0.5,1),8;[1,1.5),15;[1.5,2),22;
[2,2.5),25;[2.5,3),14;[3,3.5),6;[3.5,4),4;
[4,4.5],2.
(1)列出样本的频率分布表;
(2)画出频率直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为3t的标准,若超出标准加倍收费,当地政府说,85%以上的居民不超过这个标准,这个解释对吗?为什么?
解 (1)频率分布表.
分组 频数 频率
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1
(2)频率直方图如图.
众数:2.25;中位数:2.02;平均数:2.02.
(3)人均月用水量在3t以上的居民所占的比例为6%+4%+2%=12%,即大约有12%的居民月用水量在3t以上,88%的居民月用水量在3t以下,因此政府的解释是正确的.
1.(多选)下列说法正确的是( )
A.在统计里,把所需考察对象的全体叫作总体
B.一组数据的平均数一定大于这组数据中的每个数据
C.平均数、众数与中位数从不同的角度描述了一组数据的集中趋势
D.众数是一组数据中出现次数最多的数
答案 ACD
解析 平均数不大于最大值,不小于最小值.故B错.
2.对于数据3,3,2,3,6,3,10,3,6,3,2,下列结论正确的是( )
A.这组数据的众数是3
B.这组数据的众数与中位数的数值不相等
C.这组数据的中位数与平均数的数值相等
D.这组数据的平均数与众数的数值相等
答案 A
解析 在这11个数中,数3出现了6次,出现的次数最多,故众数是3;将这11个数按从小到大的顺序排列得2,2,3,3,3,3,3,3,6,6,10,中间数据是3,故中位数是3;而平均数==4.故只有A正确.
3.下列关于平均数、中位数、众数的说法中正确的是( )
A.中位数可以准确地反映出总体的情况
B.平均数可以准确地反映出总体的情况
C.众数可以准确地反映出总体的情况
D.平均数、中位数、众数都有局限性,都不能准确地反映出总体的情况
答案 D
4.某高校有甲、乙两个数学建模兴趣班,其中甲班40人,乙班50人.现分析两个班的一次考试成绩,算得甲班的平均成绩是90分,乙班的平均成绩是81分,则该校数学建模兴趣班的平均成绩是________分.
答案 85
解析 平均成绩为=85(分).
5.样本容量为100的频率直方图如图所示,根据样本频率直方图,得平均数为________.
答案 14.84
解析 平均数=10×0.06+12×0.1+14×0.4+16×0.24+18×0.2=14.84.
利用频率分布直方图求数字特征:
(1)众数是最高矩形的底边中点的横坐标.
(2)中位数左右两边直方图的面积应相等.
(3)平均数等于每个小矩形的面积乘以小矩形底边中点的横坐标之和.
2 / 8
14.4 用样本估计总体
14.4.1 用样本估计总体的集中趋势参数
在学习运用样本估计总体的过程中,要通过对具体数据的分析,使学生体会到由于样本数据具有随机性,样本所提供的信息在一定程度上反映了总体的有关特征,但与总体有一定的偏差.但是,如果抽样的方法比较合理,样本信息可以比较好地反映总体的信息,从而为人们合理地决策提供依据.由此使学生认识统计思维的特点和作用,体会统计思维与确定性思维的差异.
课程目标 学科素养
1.了解平均数为什么是“最理想”的近似值. 2.会计算一组数据的平均数. 3.会根据频率分布表或频率直方图估计平均数. 在学习和应用平均数、中位数和众数的过程中,要进行运算,对数据进行分析,发展学生的数学运算素养和数据分析素养.
1.教学重点:会计算一组数据的平均数.
2.教学难点:会根据频率分布表或频率直方图估计平均数.
多媒体调试、讲义分发。
现从甲、乙、丙三个厂家生产的同一种耐用家电产品中,各抽取8件产品,对其使用寿命进行跟踪调查,其结果如下:(单位:年)
甲:3,4,5,6,8,8,8,10;乙:4,6,6,6,8,9,12,13;丙:3,3,4,7,9,10,11,12.
问题 三家广告中都称其产品的使用寿命为8年,利用初中所学的知识,你能说明为什么吗?
提示 三个厂家是从不同角度进行了说明,以宣传自己的产品.其中甲:众数为8年,乙:平均数为8年,丙:中位数为8年.
知识点一 平均数
一般地,使(x-a1)2+(x-a2)2+…+(x-an)2=nx2-2(a1+a2+…+an)x+a+a+…+a最小的x=称为这n个数据a1,a2,…,an的平均数.
一般记为:=.
知识点二 平均数的估计
一般地,若取值为x1,x2,…,xn的频率分别为p1,p2,…,pn,则其平均数为=x1p1+x2p2+…+xnpn.
知识点三 众数与中位数
1.众数:一般地,将一组数据中出现次数最多的那个数据叫作该组数据的众数.
2.中位数:一般地,将一组数据按照从小到大的顺序排成一列,如果数据的个数为奇数,那么排在正中间的数据就是这组数据的中位数;如果数据的个数为偶数,那么排在正中间的两个数据的平均数即为这组数据的中位数.
一、平均数的计算
例1 (1)某班45名同学的年龄(单位:岁)如下:
14 15 14 16 15 17 16 15 16 16 15 15
17 13 14 15 16 16 15 14 15 15 14 15
16 17 16 15 15 15 16 15 13 16 15 15
17 14 15 16 16 15 14 15 15
求全班的平均年龄.
(2)从高三年级中抽出50名学生参加数学竞赛,由成绩得到如图所示的频率直方图.
试利用频率直方图估计高三年级学生的平均成绩.
解 (1)方法一 利用平均数的公式计算:
=×(14+15+…+15)=×684=15.2.
方法二 利用平均数的简化公式计算.
取a=15,将已知各数减去15,得
-1 0 -1 1 0 2 1 0 1 1 0 0 2 -2 -1 0 1 1 0 -1 0 0 -1 0 1 2 1 0 0 0 1 0 -2 1 0 0 2 -1 0 1 1 0 -1 0 0
′=×(-1+0+…+0)=×9=0.2,
=′+a=0.2+15=15.2.
方法三 利用加权平均数公式计算.
=×(13×2+14×7+15×20+16×12+17×4)
=×684=15.2.
即全班的平均年龄是15.2岁.
(2)样本平均数是频率直方图的“重心”,即所有数据的平均数,取每个小矩形底边的中点值乘以每个小矩形的面积再求和即可.
故平均成绩为
45×(0.004×10)+55×(0.006×10)+65×(0.02×10)+75×(0.03×10)+85×(0.024×10)+95×(0.016×10)=76.2(分).
反思感悟 (1)给定一组数据,要求其平均数可直接套用公式,若这组数据都在某一数据附近波动,可用平均数的简化公式计算,若这组数据某些数多次出现,可用加权平均数公式计算.
(2)在频率分布表中,平均数可用各组区间的组中值与对应频率之积进行估计.
(3)若一组数据的个数未知,但每一数据所占比例已知,可用频率平均数公式.
跟踪训练1 一批乒乓球,随机抽取100个进行检查,球的直径频率直方图如图.试估计这个样本的平均数.
解 平均数为39.96×0.1+39.98×0.2+40×0.5+40.02×0.2=39.996.
二、频率分布与数字特征的综合应用
例2 已知一组数据:
125 121 123 125 127 129 125 128 130 129
126 124 125 127 126 122 124 125 126 128
(1)填写下面的频率分布表:
分组 频数 频率
[121,123)
[123,125)
[125,127)
[127,129)
[129,131]
合计
(2)作出频率直方图;
(3)根据频率直方图或频率分布表求这组数据的众数、中位数和平均数.
解 (1)频率分布表如下.
分组 频数 频率
[121,123) 2 0.10
[123,125) 3 0.15
[125,127) 8 0.40
[127,129) 4 0.20
[129,131] 3 0.15
合计 20 1.00
(2)频率直方图如下.
(3)在[125,127)中的数据最多,取这个区间的中点值作为众数的近似值,得众数126,事实上,众数的精确值为125.图中虚线对应的数据是125+2×=126.25,事实上中位数为125.5.使用“组中值”求平均数:=122×0.1+124×0.15+126×0.4+128×0.2+130×0.15=126.3,
平均数的精确值为=125.75.
反思感悟 众数、中位数、平均数与频率分布表、频率直方图的关系
(1)众数:众数一般用频率表中频率最高的一小组的组中值来显示,即在样本数据的频率直方图中,最高矩形的底边中点的横坐标.
(2)中位数:在频率直方图中,中位数左边和右边的直方图的面积应该相等.
(3)平均数:平均数在频率分布表中等于组中值与对应频率之积的和.
注意 因为频率直方图不能体现样本数据,因此由频率直方图得到的中位数不一定在样本数据中出现.
跟踪训练2 在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(单位:m) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求这些运动员成绩的众数、中位数与平均数.
解 在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.题中表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70;这组数据的平均数是=(1.50×2+1.60×3+…+1.90×1)=≈1.69.
三、数字特征的应用
例3 某公司的33名职工的月工资(单位:元)如下表:
职位 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5 500 5 000 3 500 3 000 2 500 2 000 1 500
(1)求该公司职工月工资的平均数、中位数、众数;
(2)若董事长、副董事长的工资分别从5 500元、5 000元提升到30 000元、20 000元,那么公司职工的月工资的新的平均数、中位数和众数又是什么?
(3)你认为哪个统计量更能反映这个公司职工的工资水平?
解 (1)公司职工月工资的平均数为
=
=≈2 091.
若把所有数据从小到大排序,则得到中位数是1 500,众数是1 500.
(2)当董事长、副董事长的工资提升后,职工月工资的平均数为
=
=≈3 288.
中位数是1 500,众数是1 500.
(3)在这个问题中,中位数和众数都能反映出这个公司职工的工资水平,因为公司少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司职工的工资水平.
反思感悟 三种数字特征的比较
名称 优点 缺点
众数 ①体现了样本数据的最大集中点; ②容易计算 ①它只能表达样本数据中很少的一部分信息; ②无法客观地反映总体的特征
中位数 ①不受少数几个极端数据(即排序靠前或靠后的数据)的影响; ②容易计算,便于利用中间数据的信息 对极端值不敏感
平均数 代表性较好,是反映数据集中趋势的量.一般情况下,可以反映出更多的关于样本数据全体的信息 任何一个数据的改变都会引起平均数的改变.数据越“离群”,对平均数的影响越大
跟踪训练3 某地区100位居民的人均月用水量(单位:t)的分组及各组的频数如下:
[0,0.5),4;[0.5,1),8;[1,1.5),15;[1.5,2),22;
[2,2.5),25;[2.5,3),14;[3,3.5),6;[3.5,4),4;
[4,4.5],2.
(1)列出样本的频率分布表;
(2)画出频率直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为3t的标准,若超出标准加倍收费,当地政府说,85%以上的居民不超过这个标准,这个解释对吗?为什么?
解 (1)频率分布表.
分组 频数 频率
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1
(2)频率直方图如图.
众数:2.25;中位数:2.02;平均数:2.02.
(3)人均月用水量在3t以上的居民所占的比例为6%+4%+2%=12%,即大约有12%的居民月用水量在3t以上,88%的居民月用水量在3t以下,因此政府的解释是正确的.
1.(多选)下列说法正确的是( )
A.在统计里,把所需考察对象的全体叫作总体
B.一组数据的平均数一定大于这组数据中的每个数据
C.平均数、众数与中位数从不同的角度描述了一组数据的集中趋势
D.众数是一组数据中出现次数最多的数
答案 ACD
解析 平均数不大于最大值,不小于最小值.故B错.
2.对于数据3,3,2,3,6,3,10,3,6,3,2,下列结论正确的是( )
A.这组数据的众数是3
B.这组数据的众数与中位数的数值不相等
C.这组数据的中位数与平均数的数值相等
D.这组数据的平均数与众数的数值相等
答案 A
解析 在这11个数中,数3出现了6次,出现的次数最多,故众数是3;将这11个数按从小到大的顺序排列得2,2,3,3,3,3,3,3,6,6,10,中间数据是3,故中位数是3;而平均数==4.故只有A正确.
3.下列关于平均数、中位数、众数的说法中正确的是( )
A.中位数可以准确地反映出总体的情况
B.平均数可以准确地反映出总体的情况
C.众数可以准确地反映出总体的情况
D.平均数、中位数、众数都有局限性,都不能准确地反映出总体的情况
答案 D
4.某高校有甲、乙两个数学建模兴趣班,其中甲班40人,乙班50人.现分析两个班的一次考试成绩,算得甲班的平均成绩是90分,乙班的平均成绩是81分,则该校数学建模兴趣班的平均成绩是________分.
答案 85
解析 平均成绩为=85(分).
5.样本容量为100的频率直方图如图所示,根据样本频率直方图,得平均数为________.
答案 14.84
解析 平均数=10×0.06+12×0.1+14×0.4+16×0.24+18×0.2=14.84.
利用频率分布直方图求数字特征:
(1)众数是最高矩形的底边中点的横坐标.
(2)中位数左右两边直方图的面积应相等.
(3)平均数等于每个小矩形的面积乘以小矩形底边中点的横坐标之和.
2 / 8
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
