苏教版(2019)高中数学必修第二册 14.4.1用样本估计总体的集中趋势参数 练习(解析版)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 14.4.1用样本估计总体的集中趋势参数 练习(解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 367.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 12:18:43 | ||
图片预览



文档简介
14.4.1 用样本估计总体的集中趋势参数
1.10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
A.a>b>c B.b>c>a C.c>a>b D.c>b>a
2.某台机床加工的五批同数量的产品中次品数的频率分布如表:
次品数 0 1 2 3 4
频率 0.5 0.2 0.05 0.2 0.05
则次品数的平均数为( )
A.1.1 B.3
C.1.5 D.2
3.某学习小组在一次数学测验中,得100分的有1人,95分的有1人,90分的有2人,85分的有4人,80分和75分的各有1人,则该小组成绩的平均数为( )
A.83 B.85
C.87 D.89
4.某班全体学生参加物理测试成绩的频率直方图如图所示,则估计该班物理测试的平均成绩是( )
A.70分 B.75分
C.68分 D.66分
5.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差为( )
A.-1 B.1
C.-3 D.3
6.已知一组数据4,6,5,8,7,6,那么这组数据的平均数为________.
7.已知样本数据x1,x2,…,x10,其中x1,x2,x3的平均数为a,x4,x5,x6,…,x10的平均数为b,则样本数据的平均数为________.
8.已知一组数据按从小到大排列为-1,0,4,x,6,15,且这组数据的中位数是5,那么数据的众数是________,平均数是________.
9.某地区全体九年级的3 000名学生参加了一次科学测试,为了估计学生的成绩,从不同学校的不同程度的学生中抽取了100名学生的成绩如下:
100分12人,90分30人,80分18人,70分24人,60分12人,50分4人.
请根据以上数据估计该地区3 000名学生的平均分、合格率(60或60分以上均属合格).
10.某小区广场上有甲、乙两群市民正在进行晨练,两群市民的年龄如下(单位:岁):
甲群:13,13,14,15,15,15,15,16,17,17;
乙群:54,3,4,4,5,6,6,6,6,56.
(1)甲群市民年龄的平均数、中位数和众数各是多少?其中哪个统计量能较好地反映甲群市民的年龄特征?
(2)乙群市民年龄的平均数、中位数和众数各是多少?其中哪个统计量能较好地反映乙群市民的年龄特征?
11.有容量为100的样本,数据分组及各组的频数、频率如下:
[12.5,14.5),6,0.06;[14.5,16.5),16,0.16;[16.5,18.5),18,0.18;[18.5,20.5),22,0.22;[20.5,22.5),20,0.20;[22.5,24.5),10,0.10;[24.5,26.5],8,0.08.则估计总体的平均数为( )
A.19.40 B.19.42 C.19.44 D.19.46
12.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组,绘制成如图所示的频率直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
则估计高一参赛学生的成绩的众数、中位数分别为____________.
13.某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1∶2∶1,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共抽取100件做使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均数分别为980 h,1 020 h,1 032 h,则抽取的100件产品的使用寿命的平均数为________ h.
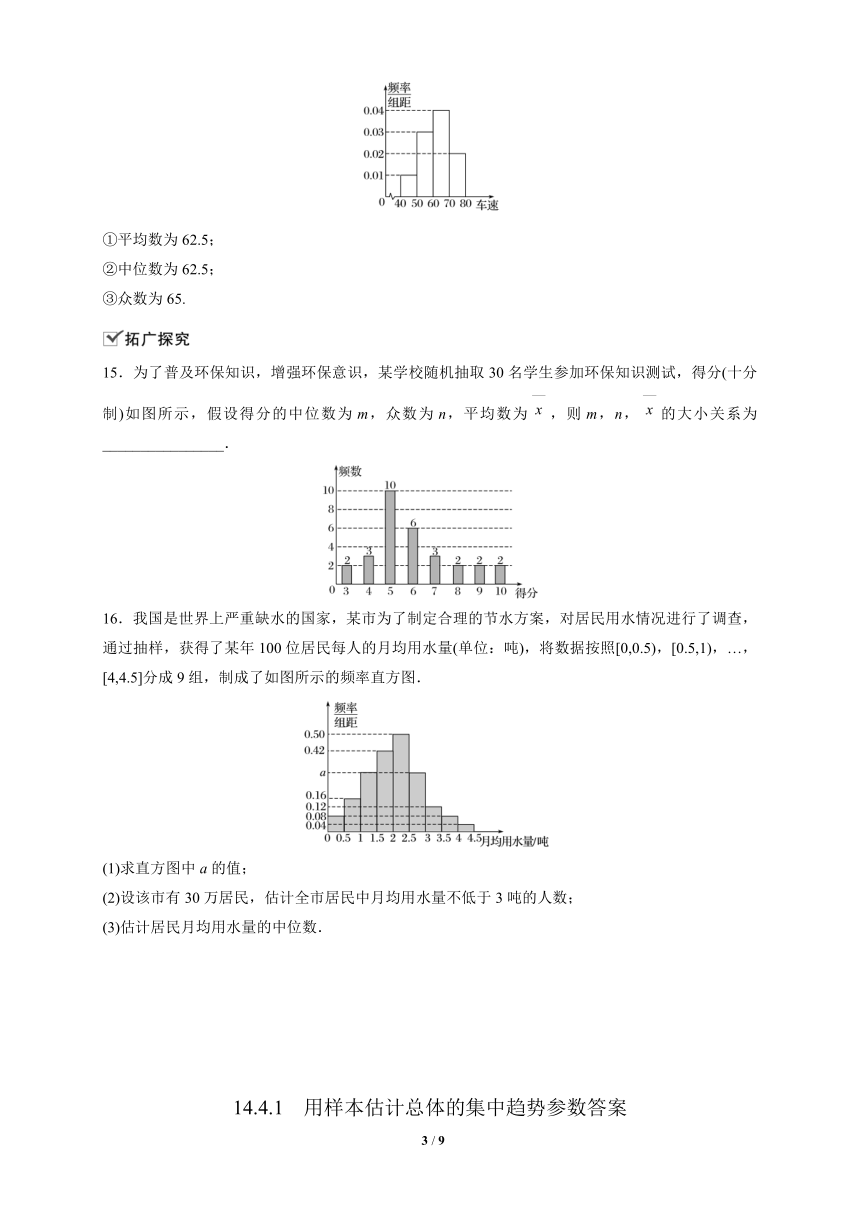
14.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率直方图,利用组中值估计,则下列说法正确的是________(填序号).
①平均数为62.5;
②中位数为62.5;
③众数为65.
15.为了普及环保知识,增强环保意识,某学校随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为m,众数为n,平均数为,则m,n,的大小关系为________________.
16.我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率直方图.
(1)求直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数;
(3)估计居民月均用水量的中位数.
14.4.1 用样本估计总体的集中趋势参数答案
1.10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
A.a>b>c B.b>c>a C.c>a>b D.c>b>a
【答案】 D
【解析】 由已知得a=×(15+17+14+10+15+17+17+16+14+12)=14.7,b=×(15+15)=15,c=17,
∴c>b>a.
2.某台机床加工的五批同数量的产品中次品数的频率分布如表:
次品数 0 1 2 3 4
频率 0.5 0.2 0.05 0.2 0.05
则次品数的平均数为( )
A.1.1 B.3
C.1.5 D.2
【答案】 A
【解析】 设数据xi出现的频率为pi(i=1,2,…,n),则x1,x2,…,xn的平均数为x1p1+x2p2+…+xnpn=0×0.5+1×0.2+2×0.05+3×0.2+4×0.05=1.1.
3.某学习小组在一次数学测验中,得100分的有1人,95分的有1人,90分的有2人,85分的有4人,80分和75分的各有1人,则该小组成绩的平均数为( )
A.83 B.85
C.87 D.89
【答案】 C
【解析】 平均数是×(100+95+2×90+4×85+80+75)=87.
∴平均数是87.
4.某班全体学生参加物理测试成绩的频率直方图如图所示,则估计该班物理测试的平均成绩是( )
A.70分 B.75分
C.68分 D.66分
【答案】 C
【解析】 平均成绩就是频率直方图中每个小矩形的面积乘以小矩形底边中点的横坐标再求和,即0.005×20×30+0.01×20×50+0.02×20×70+0.015×20×90=68(分).
5.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差为( )
A.-1 B.1
C.-3 D.3
【答案】 C
【解析】 少输入90,=3,平均数少3,求出的平均数减去实际的平均数等于-3.
6.已知一组数据4,6,5,8,7,6,那么这组数据的平均数为________.
【答案】 6
【解析】 由已知得,所求平均数为=6.
7.已知样本数据x1,x2,…,x10,其中x1,x2,x3的平均数为a,x4,x5,x6,…,x10的平均数为b,则样本数据的平均数为________.
【答案】
【解析】 前3个数据的和为3a,后7个数据的和为7b,样本平均数为10个数据的和除以10,即.
8.已知一组数据按从小到大排列为-1,0,4,x,6,15,且这组数据的中位数是5,那么数据的众数是________,平均数是________.
【答案】 6 5
【解析】 ∵中位数为5,∴=5,即x=6.
∴该组数据的众数为6,平均数为=5.
9.某地区全体九年级的3 000名学生参加了一次科学测试,为了估计学生的成绩,从不同学校的不同程度的学生中抽取了100名学生的成绩如下:
100分12人,90分30人,80分18人,70分24人,60分12人,50分4人.
请根据以上数据估计该地区3 000名学生的平均分、合格率(60或60分以上均属合格).
解 平均分为
=79.4(分),
(12+30+18+24+12)÷100×100%=96%,
所以样本的平均分是79.4分,合格率是96%,由此来估计总体3 000名学生的平均分是79.4分,合格率是96%.
10.某小区广场上有甲、乙两群市民正在进行晨练,两群市民的年龄如下(单位:岁):
甲群:13,13,14,15,15,15,15,16,17,17;
乙群:54,3,4,4,5,6,6,6,6,56.
(1)甲群市民年龄的平均数、中位数和众数各是多少?其中哪个统计量能较好地反映甲群市民的年龄特征?
(2)乙群市民年龄的平均数、中位数和众数各是多少?其中哪个统计量能较好地反映乙群市民的年龄特征?
解 (1)甲群市民年龄的平均数为
=15,中位数为15,众数为15.
平均数、中位数和众数相等,因此它们都能较好地反映甲群市民的年龄特征.
(2)乙群市民年龄的平均数为
=15,中位数为6,众数为6.
由于乙群市民大多数是儿童,所以中位数和众数能较好地反映乙群市民的年龄特征,而平均数的可靠性较差.
11.有容量为100的样本,数据分组及各组的频数、频率如下:
[12.5,14.5),6,0.06;[14.5,16.5),16,0.16;[16.5,18.5),18,0.18;[18.5,20.5),22,0.22;[20.5,22.5),20,0.20;[22.5,24.5),10,0.10;[24.5,26.5],8,0.08.则估计总体的平均数为( )
A.19.40 B.19.42 C.19.44 D.19.46
【答案】 B
【解析】 由于每组数据是一个范围,所以可以用组中值近似地表示平均数.
方法一 总体的平均数约为(13.5×6+15.5×16+17.5×18+19.5×22+21.5×20+23.5×10+25.5×8)=19.42.
故总体的平均数约为19.42.
方法二 组中值与对应频率积的和为13.5×0.06+15.5×0.16+17.5×0.18+19.5×0.22+21.5×0.20+23.5×0.10+25.5×0.08=19.42.
故总体的平均数约为19.42.
12.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组,绘制成如图所示的频率直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
则估计高一参赛学生的成绩的众数、中位数分别为____________.
【答案】 65,65
【解析】 由题图可知众数为65,
又∵第一个小矩形的面积为0.3,
∴设中位数为60+x,则0.3+x×0.04=0.5,得x=5,
∴中位数为60+5=65.
13.某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1∶2∶1,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共抽取100件做使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均数分别为980 h,1 020 h,1 032 h,则抽取的100件产品的使用寿命的平均数为________ h.
【答案】 1 013
【解析】 依题意可知平均数
==1 013.
14.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率直方图,利用组中值估计,则下列说法正确的是________(填序号).
①平均数为62.5;
②中位数为62.5;
③众数为65.
【答案】 ②③
【解析】 由频率直方图可知,平均数为0.01×10×45+0.03×10×55+0.04×10×65+0.02×10×75=62.
设中位数为a,由题意得0.01×10+0.03×10+0.04×(a-60)=0.5,解得a=62.5.
众数为频率直方图中最高矩形底边中点值,故其众数为65.
15.为了普及环保知识,增强环保意识,某学校随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为m,众数为n,平均数为,则m,n,的大小关系为________________.
【答案】 n<m<
【解析】 由题目所给的统计图可知,30个数据按从小到大的顺序排列好后,中间两个数为5,6,故中位数为m==5.5.
又众数为n=5,平均数=
=.所以n<m<.
16.我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率直方图.
(1)求直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数;
(3)估计居民月均用水量的中位数.
解 (1)由频率直方图可知,月均用水量在[0,0.5)的频率为0.08×0.5=0.04.
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)
=0.5×a+0.5×a,
解得a=0.30.
(2)由(1)知,100位居民月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12.由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为300 000×0.12=36 000.
(3)设中位数为x.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5.
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5.
所以2≤x<2.5.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04.
1 / 9
1.10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
A.a>b>c B.b>c>a C.c>a>b D.c>b>a
2.某台机床加工的五批同数量的产品中次品数的频率分布如表:
次品数 0 1 2 3 4
频率 0.5 0.2 0.05 0.2 0.05
则次品数的平均数为( )
A.1.1 B.3
C.1.5 D.2
3.某学习小组在一次数学测验中,得100分的有1人,95分的有1人,90分的有2人,85分的有4人,80分和75分的各有1人,则该小组成绩的平均数为( )
A.83 B.85
C.87 D.89
4.某班全体学生参加物理测试成绩的频率直方图如图所示,则估计该班物理测试的平均成绩是( )
A.70分 B.75分
C.68分 D.66分
5.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差为( )
A.-1 B.1
C.-3 D.3
6.已知一组数据4,6,5,8,7,6,那么这组数据的平均数为________.
7.已知样本数据x1,x2,…,x10,其中x1,x2,x3的平均数为a,x4,x5,x6,…,x10的平均数为b,则样本数据的平均数为________.
8.已知一组数据按从小到大排列为-1,0,4,x,6,15,且这组数据的中位数是5,那么数据的众数是________,平均数是________.
9.某地区全体九年级的3 000名学生参加了一次科学测试,为了估计学生的成绩,从不同学校的不同程度的学生中抽取了100名学生的成绩如下:
100分12人,90分30人,80分18人,70分24人,60分12人,50分4人.
请根据以上数据估计该地区3 000名学生的平均分、合格率(60或60分以上均属合格).
10.某小区广场上有甲、乙两群市民正在进行晨练,两群市民的年龄如下(单位:岁):
甲群:13,13,14,15,15,15,15,16,17,17;
乙群:54,3,4,4,5,6,6,6,6,56.
(1)甲群市民年龄的平均数、中位数和众数各是多少?其中哪个统计量能较好地反映甲群市民的年龄特征?
(2)乙群市民年龄的平均数、中位数和众数各是多少?其中哪个统计量能较好地反映乙群市民的年龄特征?
11.有容量为100的样本,数据分组及各组的频数、频率如下:
[12.5,14.5),6,0.06;[14.5,16.5),16,0.16;[16.5,18.5),18,0.18;[18.5,20.5),22,0.22;[20.5,22.5),20,0.20;[22.5,24.5),10,0.10;[24.5,26.5],8,0.08.则估计总体的平均数为( )
A.19.40 B.19.42 C.19.44 D.19.46
12.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组,绘制成如图所示的频率直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
则估计高一参赛学生的成绩的众数、中位数分别为____________.
13.某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1∶2∶1,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共抽取100件做使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均数分别为980 h,1 020 h,1 032 h,则抽取的100件产品的使用寿命的平均数为________ h.
14.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率直方图,利用组中值估计,则下列说法正确的是________(填序号).
①平均数为62.5;
②中位数为62.5;
③众数为65.
15.为了普及环保知识,增强环保意识,某学校随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为m,众数为n,平均数为,则m,n,的大小关系为________________.
16.我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率直方图.
(1)求直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数;
(3)估计居民月均用水量的中位数.
14.4.1 用样本估计总体的集中趋势参数答案
1.10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
A.a>b>c B.b>c>a C.c>a>b D.c>b>a
【答案】 D
【解析】 由已知得a=×(15+17+14+10+15+17+17+16+14+12)=14.7,b=×(15+15)=15,c=17,
∴c>b>a.
2.某台机床加工的五批同数量的产品中次品数的频率分布如表:
次品数 0 1 2 3 4
频率 0.5 0.2 0.05 0.2 0.05
则次品数的平均数为( )
A.1.1 B.3
C.1.5 D.2
【答案】 A
【解析】 设数据xi出现的频率为pi(i=1,2,…,n),则x1,x2,…,xn的平均数为x1p1+x2p2+…+xnpn=0×0.5+1×0.2+2×0.05+3×0.2+4×0.05=1.1.
3.某学习小组在一次数学测验中,得100分的有1人,95分的有1人,90分的有2人,85分的有4人,80分和75分的各有1人,则该小组成绩的平均数为( )
A.83 B.85
C.87 D.89
【答案】 C
【解析】 平均数是×(100+95+2×90+4×85+80+75)=87.
∴平均数是87.
4.某班全体学生参加物理测试成绩的频率直方图如图所示,则估计该班物理测试的平均成绩是( )
A.70分 B.75分
C.68分 D.66分
【答案】 C
【解析】 平均成绩就是频率直方图中每个小矩形的面积乘以小矩形底边中点的横坐标再求和,即0.005×20×30+0.01×20×50+0.02×20×70+0.015×20×90=68(分).
5.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差为( )
A.-1 B.1
C.-3 D.3
【答案】 C
【解析】 少输入90,=3,平均数少3,求出的平均数减去实际的平均数等于-3.
6.已知一组数据4,6,5,8,7,6,那么这组数据的平均数为________.
【答案】 6
【解析】 由已知得,所求平均数为=6.
7.已知样本数据x1,x2,…,x10,其中x1,x2,x3的平均数为a,x4,x5,x6,…,x10的平均数为b,则样本数据的平均数为________.
【答案】
【解析】 前3个数据的和为3a,后7个数据的和为7b,样本平均数为10个数据的和除以10,即.
8.已知一组数据按从小到大排列为-1,0,4,x,6,15,且这组数据的中位数是5,那么数据的众数是________,平均数是________.
【答案】 6 5
【解析】 ∵中位数为5,∴=5,即x=6.
∴该组数据的众数为6,平均数为=5.
9.某地区全体九年级的3 000名学生参加了一次科学测试,为了估计学生的成绩,从不同学校的不同程度的学生中抽取了100名学生的成绩如下:
100分12人,90分30人,80分18人,70分24人,60分12人,50分4人.
请根据以上数据估计该地区3 000名学生的平均分、合格率(60或60分以上均属合格).
解 平均分为
=79.4(分),
(12+30+18+24+12)÷100×100%=96%,
所以样本的平均分是79.4分,合格率是96%,由此来估计总体3 000名学生的平均分是79.4分,合格率是96%.
10.某小区广场上有甲、乙两群市民正在进行晨练,两群市民的年龄如下(单位:岁):
甲群:13,13,14,15,15,15,15,16,17,17;
乙群:54,3,4,4,5,6,6,6,6,56.
(1)甲群市民年龄的平均数、中位数和众数各是多少?其中哪个统计量能较好地反映甲群市民的年龄特征?
(2)乙群市民年龄的平均数、中位数和众数各是多少?其中哪个统计量能较好地反映乙群市民的年龄特征?
解 (1)甲群市民年龄的平均数为
=15,中位数为15,众数为15.
平均数、中位数和众数相等,因此它们都能较好地反映甲群市民的年龄特征.
(2)乙群市民年龄的平均数为
=15,中位数为6,众数为6.
由于乙群市民大多数是儿童,所以中位数和众数能较好地反映乙群市民的年龄特征,而平均数的可靠性较差.
11.有容量为100的样本,数据分组及各组的频数、频率如下:
[12.5,14.5),6,0.06;[14.5,16.5),16,0.16;[16.5,18.5),18,0.18;[18.5,20.5),22,0.22;[20.5,22.5),20,0.20;[22.5,24.5),10,0.10;[24.5,26.5],8,0.08.则估计总体的平均数为( )
A.19.40 B.19.42 C.19.44 D.19.46
【答案】 B
【解析】 由于每组数据是一个范围,所以可以用组中值近似地表示平均数.
方法一 总体的平均数约为(13.5×6+15.5×16+17.5×18+19.5×22+21.5×20+23.5×10+25.5×8)=19.42.
故总体的平均数约为19.42.
方法二 组中值与对应频率积的和为13.5×0.06+15.5×0.16+17.5×0.18+19.5×0.22+21.5×0.20+23.5×0.10+25.5×0.08=19.42.
故总体的平均数约为19.42.
12.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组,绘制成如图所示的频率直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
则估计高一参赛学生的成绩的众数、中位数分别为____________.
【答案】 65,65
【解析】 由题图可知众数为65,
又∵第一个小矩形的面积为0.3,
∴设中位数为60+x,则0.3+x×0.04=0.5,得x=5,
∴中位数为60+5=65.
13.某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1∶2∶1,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共抽取100件做使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均数分别为980 h,1 020 h,1 032 h,则抽取的100件产品的使用寿命的平均数为________ h.
【答案】 1 013
【解析】 依题意可知平均数
==1 013.
14.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率直方图,利用组中值估计,则下列说法正确的是________(填序号).
①平均数为62.5;
②中位数为62.5;
③众数为65.
【答案】 ②③
【解析】 由频率直方图可知,平均数为0.01×10×45+0.03×10×55+0.04×10×65+0.02×10×75=62.
设中位数为a,由题意得0.01×10+0.03×10+0.04×(a-60)=0.5,解得a=62.5.
众数为频率直方图中最高矩形底边中点值,故其众数为65.
15.为了普及环保知识,增强环保意识,某学校随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为m,众数为n,平均数为,则m,n,的大小关系为________________.
【答案】 n<m<
【解析】 由题目所给的统计图可知,30个数据按从小到大的顺序排列好后,中间两个数为5,6,故中位数为m==5.5.
又众数为n=5,平均数=
=.所以n<m<.
16.我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率直方图.
(1)求直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数;
(3)估计居民月均用水量的中位数.
解 (1)由频率直方图可知,月均用水量在[0,0.5)的频率为0.08×0.5=0.04.
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)
=0.5×a+0.5×a,
解得a=0.30.
(2)由(1)知,100位居民月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12.由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为300 000×0.12=36 000.
(3)设中位数为x.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5.
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5.
所以2≤x<2.5.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04.
1 / 9
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
