内蒙古赤峰市元宝山区第一高级中学2022-2023学年高二上学期期中考试数学试题(Word版含答案)
文档属性
| 名称 | 内蒙古赤峰市元宝山区第一高级中学2022-2023学年高二上学期期中考试数学试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 387.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 00:00:00 | ||
图片预览

文档简介
元宝山区第一高级中学2022-2023学年高二上学期期中考试
数学试卷
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的
1. 直线的倾斜角为
A. 0o B. 45o C. 90o D. 不存在
2. 如图是根据的观测数据得到的散点图,可以判断变量,具有线性相关关系的图是( )
A. ①② B. ③④ C. ②③ D. ①④
3. 演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A. 中位数 B. 平均数
C. 方差 D. 极差
4. 若点A(4,3),B(5,a),C(6,5)三点共线,则a的值为( )
A. -4 B. 4 C. D. 不存在
5. 采用系统抽样方法,从个体数为1001的总体中抽取一个容量为40的样本,则在抽取过程中,每个个体被抽到的概率为( )
A. B. C. D.
6. 从装有2个红球和2个白球的口袋内任取2个球,互斥而不对立的两个事件是( )
A. 至少有1个白球;都是白球 B. 至少有1个白球;至少有1个红球
C. 恰有1个白球;恰有2个白球 D. 至少有1个白球;都是红球
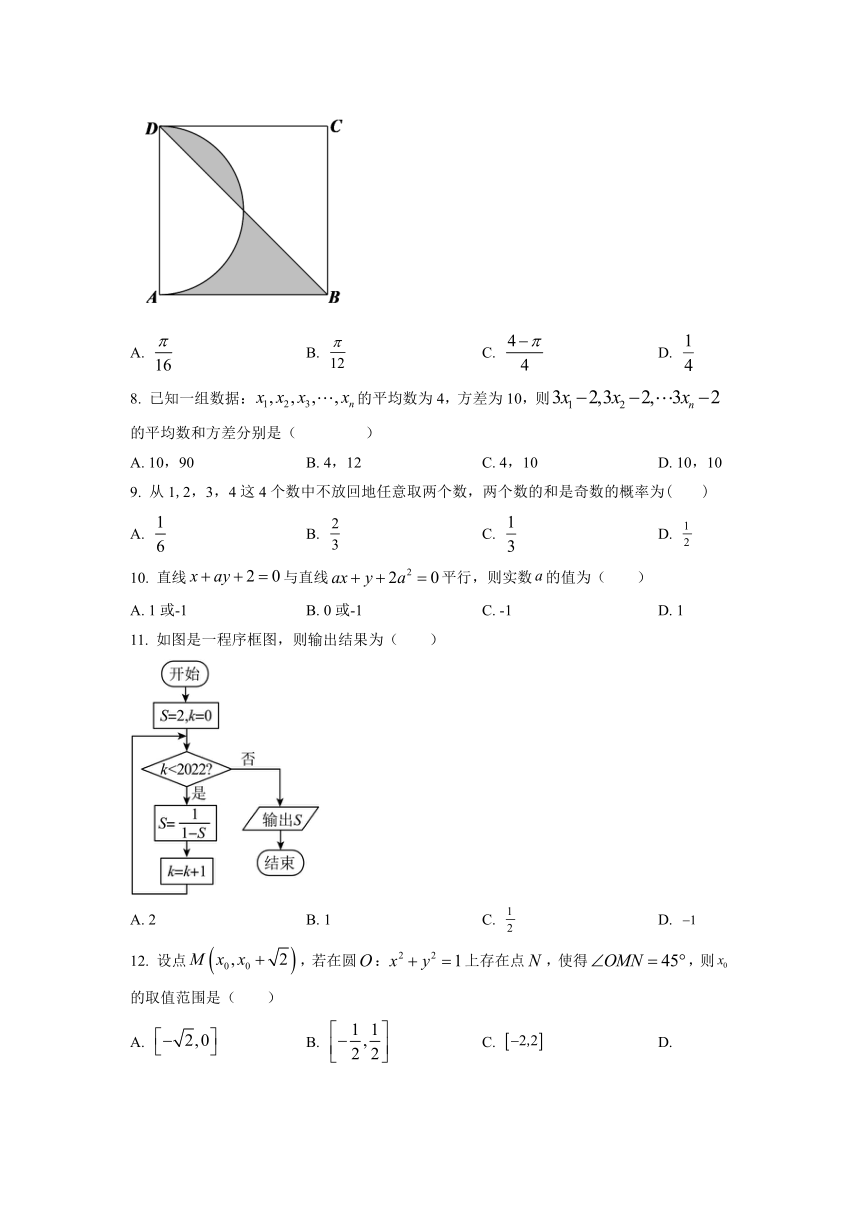
7. 在正方形中,弧是以为直径半圆,若在正方形中任取一点,则该点取自阴影部分内的概率为( )
A. B. C. D.
8. 已知一组数据:的平均数为4,方差为10,则的平均数和方差分别是( )
A. 10,90 B. 4,12 C. 4,10 D. 10,10
9. 从1,2,3,4这4个数中不放回地任意取两个数,两个数的和是奇数的概率为( )
A. B. C. D.
10. 直线与直线平行,则实数的值为( )
A. 1或-1 B. 0或-1 C. -1 D. 1
11. 如图是一程序框图,则输出结果为( )
A. 2 B. 1 C. D.
12. 设点,若在圆:上存在点,使得,则的取值范围是( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分.请将答案填在答题卡对应题号的位置上
13. 现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7, 8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为__________.
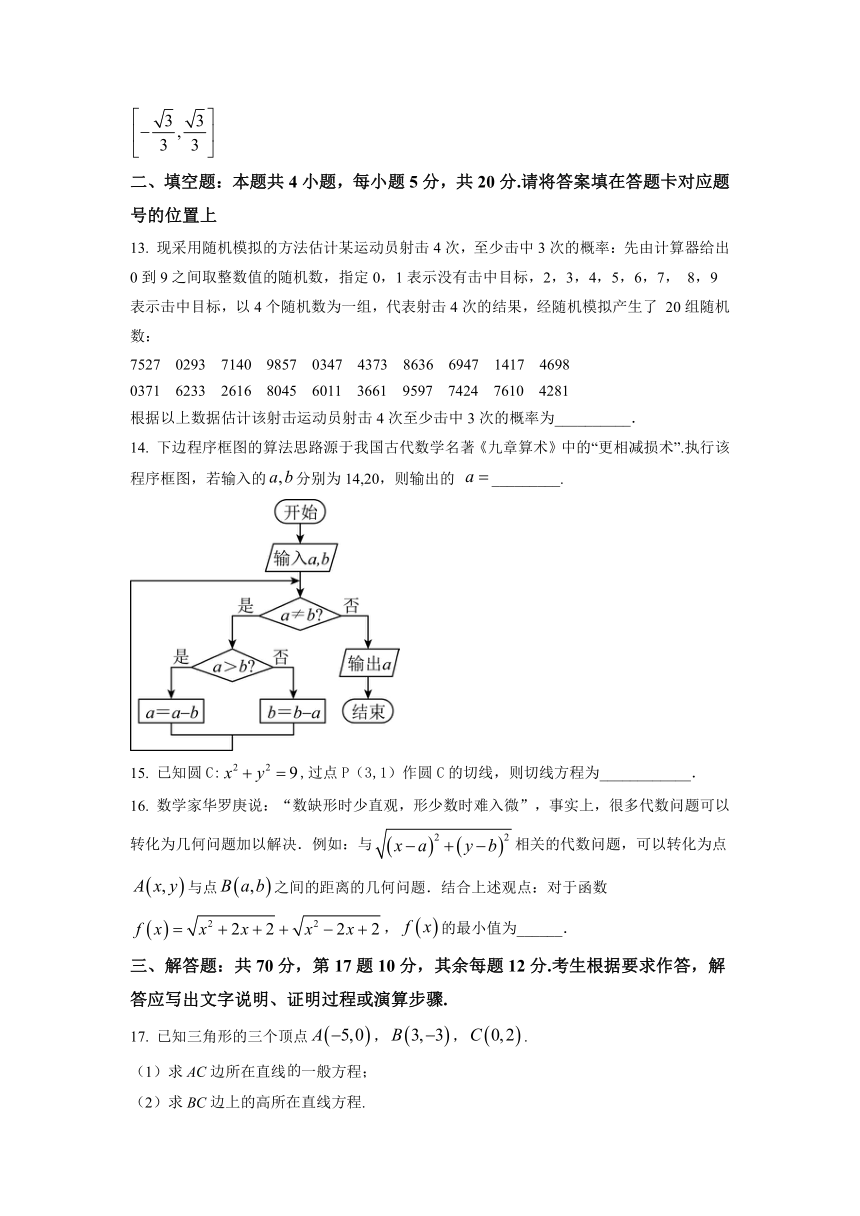
14. 下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的分别为14,20,则输出的 _________.
15. 已知圆C:,过点P(3,1)作圆C的切线,则切线方程为____________.
16. 数学家华罗庚说:“数缺形时少直观,形少数时难入微”,事实上,很多代数问题可以转化为几何问题加以解决.例如:与相关的代数问题,可以转化为点与点之间的距离的几何问题.结合上述观点:对于函数,的最小值为______.
三、解答题:共70分,第17题10分,其余每题12分.考生根据要求作答,解答应写出文字说明、证明过程或演算步骤.
17. 已知三角形的三个顶点,,.
(1)求AC边所在直线一般方程;
(2)求BC边上的高所在直线方程.
18. 一盒中装有12个球,其中5个红球,4个黑球,2个白球,1个绿球.从中随机取出1球,求:
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球概率.
19. 为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,从两厂各随机选取了个轮胎,将每个轮胎的宽度(单位:)记录下来并绘制出如下的折线图:
(1)分别计算甲、乙两厂提供的个轮胎宽度的平均值;
(2)若轮胎的宽度在内,则称这个轮胎是标准轮胎.根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个的轮胎相对更好.
20. 某公司为提高市场销售业绩,促进某产品的销售,随机调查了该产品的月销售单价(单位:元件)及相应月销量(单位:万件),对近个月的月销售单价和月销售量的数据进行了统计,得到如下表数据:
月销售单价(元/件)
月销售量(万件)
(1)建立关于的回归直线方程
(2)该公司开展促销活动,当该产品月销售单价为元/件时,其月销售量达到万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过万件,则认为所得到的回归直线方程是理想的,试问:(1)中得到的回归直线方程是否理想?
参考公式:回归直线方程,其中,参者数据:,.
21. 某校命制了一套调查问卷(试卷满分均为100分),并对整个学校的学生进行了测试.现从这些学生的成绩中随机抽取了50名学生的成绩,按照,.…,分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
(1)求频率分布直方图中x的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)用样本估计总体,若该校共有1000名学生,试估计该校这次测试成绩不低于70分的人数;
(3)若利用分层抽样的方法从样本中成绩不低于70分的学生中抽取6人,再从这6人中随机抽取3人,试求成绩在的学生至少有1人被抽到的概率.
22. 已知圆C经过,两点,且圆心在直线上.
(1)求圆C的标准方程;
(2)设直线l经过点,且l与圆C相交所得弦长为,求直线l的方程;
(3)若Q是直线上的动点,过点Q做圆C的两条切线QM、QN,切点分别为M、N,探究:直线MN是否恒过定点.若存在请写出坐标;若不存在请说明理由.
元宝山区第一高级中学2022-2023学年高二上学期期中考试
数学试卷 答案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的
【1题答案】
【答案】C
【2题答案】
【答案】B
【3题答案】
【答案】A
【4题答案】
【答案】B
【5题答案】
【答案】A
【6题答案】
【答案】C
【7题答案】
【答案】D
【8题答案】
【答案】A
【9题答案】
【答案】B
【10题答案】
【答案】C
【11题答案】
【答案】A
【12题答案】
【答案】A
二、填空题:本题共4小题,每小题5分,共20分.请将答案填在答题卡对应题号的位置上
【13题答案】
【答案】
【14题答案】
【答案】2
【15题答案】
【答案】或
【16题答案】
【答案】
三、解答题:共70分,第17题10分,其余每题12分.考生根据要求作答,解答应写出文字说明、证明过程或演算步骤.
【17题答案】
【答案】(1)
(2)
【18题答案】
【答案】(1)取出球为红球或黑球的概率为 (2)取出球为红球或黑球或白球的概率为
【19题答案】
【答案】(1)甲厂平均值为,乙厂平均值为
(2)乙厂的轮胎相对更好
【20题答案】
【答案】(1);(2)可以认为所得到的回归直线方程是理想的.
【21题答案】
【答案】(1),平均数为74分,中位数分;
(2)600 (3)
【22题答案】
【答案】(1)
(2)或.
(3)过定点
数学试卷
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的
1. 直线的倾斜角为
A. 0o B. 45o C. 90o D. 不存在
2. 如图是根据的观测数据得到的散点图,可以判断变量,具有线性相关关系的图是( )
A. ①② B. ③④ C. ②③ D. ①④
3. 演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A. 中位数 B. 平均数
C. 方差 D. 极差
4. 若点A(4,3),B(5,a),C(6,5)三点共线,则a的值为( )
A. -4 B. 4 C. D. 不存在
5. 采用系统抽样方法,从个体数为1001的总体中抽取一个容量为40的样本,则在抽取过程中,每个个体被抽到的概率为( )
A. B. C. D.
6. 从装有2个红球和2个白球的口袋内任取2个球,互斥而不对立的两个事件是( )
A. 至少有1个白球;都是白球 B. 至少有1个白球;至少有1个红球
C. 恰有1个白球;恰有2个白球 D. 至少有1个白球;都是红球
7. 在正方形中,弧是以为直径半圆,若在正方形中任取一点,则该点取自阴影部分内的概率为( )
A. B. C. D.
8. 已知一组数据:的平均数为4,方差为10,则的平均数和方差分别是( )
A. 10,90 B. 4,12 C. 4,10 D. 10,10
9. 从1,2,3,4这4个数中不放回地任意取两个数,两个数的和是奇数的概率为( )
A. B. C. D.
10. 直线与直线平行,则实数的值为( )
A. 1或-1 B. 0或-1 C. -1 D. 1
11. 如图是一程序框图,则输出结果为( )
A. 2 B. 1 C. D.
12. 设点,若在圆:上存在点,使得,则的取值范围是( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分.请将答案填在答题卡对应题号的位置上
13. 现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7, 8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为__________.
14. 下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的分别为14,20,则输出的 _________.
15. 已知圆C:,过点P(3,1)作圆C的切线,则切线方程为____________.
16. 数学家华罗庚说:“数缺形时少直观,形少数时难入微”,事实上,很多代数问题可以转化为几何问题加以解决.例如:与相关的代数问题,可以转化为点与点之间的距离的几何问题.结合上述观点:对于函数,的最小值为______.
三、解答题:共70分,第17题10分,其余每题12分.考生根据要求作答,解答应写出文字说明、证明过程或演算步骤.
17. 已知三角形的三个顶点,,.
(1)求AC边所在直线一般方程;
(2)求BC边上的高所在直线方程.
18. 一盒中装有12个球,其中5个红球,4个黑球,2个白球,1个绿球.从中随机取出1球,求:
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球概率.
19. 为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,从两厂各随机选取了个轮胎,将每个轮胎的宽度(单位:)记录下来并绘制出如下的折线图:
(1)分别计算甲、乙两厂提供的个轮胎宽度的平均值;
(2)若轮胎的宽度在内,则称这个轮胎是标准轮胎.根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个的轮胎相对更好.
20. 某公司为提高市场销售业绩,促进某产品的销售,随机调查了该产品的月销售单价(单位:元件)及相应月销量(单位:万件),对近个月的月销售单价和月销售量的数据进行了统计,得到如下表数据:
月销售单价(元/件)
月销售量(万件)
(1)建立关于的回归直线方程
(2)该公司开展促销活动,当该产品月销售单价为元/件时,其月销售量达到万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过万件,则认为所得到的回归直线方程是理想的,试问:(1)中得到的回归直线方程是否理想?
参考公式:回归直线方程,其中,参者数据:,.
21. 某校命制了一套调查问卷(试卷满分均为100分),并对整个学校的学生进行了测试.现从这些学生的成绩中随机抽取了50名学生的成绩,按照,.…,分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
(1)求频率分布直方图中x的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)用样本估计总体,若该校共有1000名学生,试估计该校这次测试成绩不低于70分的人数;
(3)若利用分层抽样的方法从样本中成绩不低于70分的学生中抽取6人,再从这6人中随机抽取3人,试求成绩在的学生至少有1人被抽到的概率.
22. 已知圆C经过,两点,且圆心在直线上.
(1)求圆C的标准方程;
(2)设直线l经过点,且l与圆C相交所得弦长为,求直线l的方程;
(3)若Q是直线上的动点,过点Q做圆C的两条切线QM、QN,切点分别为M、N,探究:直线MN是否恒过定点.若存在请写出坐标;若不存在请说明理由.
元宝山区第一高级中学2022-2023学年高二上学期期中考试
数学试卷 答案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的
【1题答案】
【答案】C
【2题答案】
【答案】B
【3题答案】
【答案】A
【4题答案】
【答案】B
【5题答案】
【答案】A
【6题答案】
【答案】C
【7题答案】
【答案】D
【8题答案】
【答案】A
【9题答案】
【答案】B
【10题答案】
【答案】C
【11题答案】
【答案】A
【12题答案】
【答案】A
二、填空题:本题共4小题,每小题5分,共20分.请将答案填在答题卡对应题号的位置上
【13题答案】
【答案】
【14题答案】
【答案】2
【15题答案】
【答案】或
【16题答案】
【答案】
三、解答题:共70分,第17题10分,其余每题12分.考生根据要求作答,解答应写出文字说明、证明过程或演算步骤.
【17题答案】
【答案】(1)
(2)
【18题答案】
【答案】(1)取出球为红球或黑球的概率为 (2)取出球为红球或黑球或白球的概率为
【19题答案】
【答案】(1)甲厂平均值为,乙厂平均值为
(2)乙厂的轮胎相对更好
【20题答案】
【答案】(1);(2)可以认为所得到的回归直线方程是理想的.
【21题答案】
【答案】(1),平均数为74分,中位数分;
(2)600 (3)
【22题答案】
【答案】(1)
(2)或.
(3)过定点
同课章节目录
