【新课标】2.1圆的对称性 课件(共35张PPT)
文档属性
| 名称 | 【新课标】2.1圆的对称性 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 15:50:09 | ||
图片预览











文档简介
(共35张PPT)
2.1圆的对称性
湘教版 九年级下
教学内容分析
在小学学习圆的基础上,进一步熟悉圆的概念,知道圆的半径、直径、弦、弧基本的概念,并且认识到圆既是轴对称图形,又是中心对称图形;本节还将学习点与圆的位置关系。本节的内容为后面的学习提供了基础知识。
教学目标
1.熟悉圆、圆心、半径、直径、弦、弧、等圆等概念;(重点)
2.知道圆是中心对称图形也是轴对称图形;
3.依据点到圆心的距离(d)和半径(r)的关系,判定点与圆的位置关系;掌握平面内的点与圆的位置关系及其条件.(重难点)
核心素养分析
本节内容是对几何图形--圆的认识,学生在本节内容学习到圆的概念,圆的对称性,以及圆心的距离(d)和半径(r)的关系,学生通过这些基础内容的认识,可以
培养几何直观的核心素养。
新知导入
同学们,你们在游乐场坐过摩天轮吗?它是什么形状呢?
圆
新知讲解
观察
在生活中, 我们经常看到圆的形象(如图 2-1)
图2-1
新知讲解
圆(circle)是平面内到一定点的距离等于定长的所有点组成的图形,
这个定点叫作圆心(center of a circle),
定长叫作半径(radius).
圆的静态定义
新知讲解
如图2-2,点O是圆心,圆心O与圆上一点的连线段叫作半径,线段OA是一条半径,
线段OA的长度也叫作半径,记作半径r.
以点O为圆心的圆叫作圆O,记作⊙O.
图2-2
注意:
1、确定圆的两个条件:圆心和半径,
圆心确定圆的位置,半径确定圆的大小;
2、圆指圆周,而非圆面.
新知讲解
新知讲解
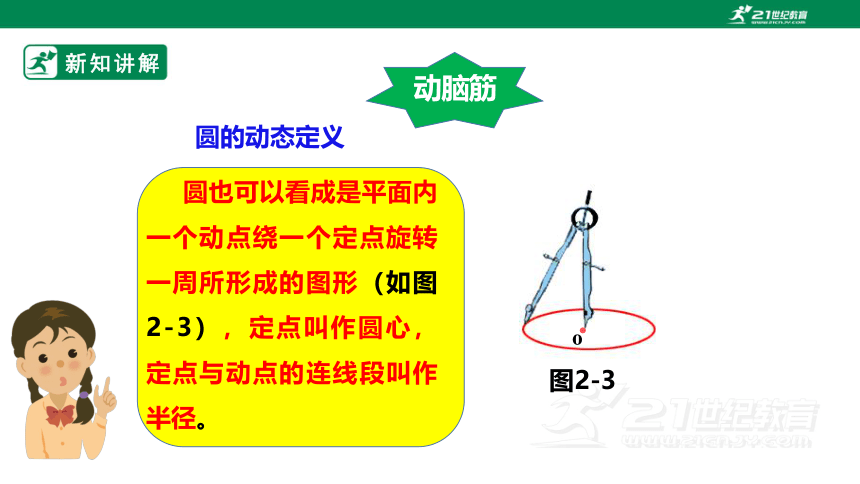
动脑筋
圆也可以看成是平面内一个动点绕一个定点旋转一周所形成的图形(如图2-3),定点叫作圆心,定点与动点的连线段叫作半径。
o
圆的动态定义
图2-3
新知讲解
平面内的点与圆有什么位置关系呢?
我们把到圆心的距离小于半径的点叫作圆内的点; 到圆心的距离大于半径的点叫作圆外的点.
新知讲解
你能说出同一平面内的点与圆有几种位置关系? 怎样确定点与圆的位置关系? 请与同学交流.
新知讲解
一般地,设⊙O的半径为r,点P到圆心O的距离OP=d,
则有:
(1)点P在圆内 d<r;
(2)点P在圆上 d=r;
(3)点P在圆外 d>r.
●
O
●
●
●
P
P
C
P
r
新知讲解
圆的其他概念
连接圆上任意两点的线段叫作弦,经过圆心的弦叫作直径.
如图2-4,线段AB,CD是⊙O的弦,
弦AB经过圆心O,
因此线段AB是⊙O的直径。
O
D
C
A
B
·
图2-4
新知讲解
易错点:
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
新知讲解
圆上任意两点间的部分叫作圆弧,简称弧,弧用符号“︵” 表示。
如图2-5,⊙O上两点A,B间小于半圆的部分叫作劣弧, 记作 ;
A,B间大于半圆的部分叫作优弧 , 记作 ,
.
O
M
A
B
·
·
⌒
AB
⌒
AMB
图2-5
新知讲解
1. 如图2-6,在一块硬纸板和一张薄的白纸上分别画一个圆,使它们的半径相等,把白纸放在硬纸板上面, 使两个圆的圆心重合,观察这两个圆是否重合.
探究
图2-6
新知讲解
2.如图2-7,用一根大头针穿过上述两个圆的圆心.让硬纸板保持不动,让白纸绕圆心旋转任意角度.观察旋转后白纸上的圆是否仍然与硬纸板上的圆重合. 这体现圆具有什么样的性质?
图2-7
只有在同圆或等圆中才存在等弧,在大小不等的两个圆中不存在等弧。
在判断等弧时,首先要看两弧所在的圆是否为同圆或等圆,然后再看弧的长度是否相等.
新知讲解
我们把能够重合的两个圆叫作等圆,把能够互相重合的弧叫作等弧.
由于圆是由一个动点绕一个定点旋转一周所形成的图形,因此圆绕圆心旋转任意角度,都能与自身重合.
特别地,将圆绕圆心旋转180°时能与自身重合,所以,
新知讲解
圆是中心对称图形,圆心是它的对称中心
新知讲解
如图2-8,在纸上任画一个⊙O,并剪下来. 将⊙O沿任意一条直径(例如直径 CD)对折,你发现了什么?
说一说
直径CD两侧的两个半圆能完全重合。
图2-8
新知讲解
圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
新知讲解
易错点:
①圆的对称轴有无数条;
②因为直径是弦,弦是线段,而对称轴是直线,所以不能说“圆的对称轴是直径”,而应该说“圆的对称轴是直径所在的直线”.
新知讲解
如图2-9,为什么通常要把车轮设计成圆形?请说明理由.
议一议
图2-9
车轮做成圆形的主要原因是省力和平稳.
1.下列说法中,不正确的是( )
A. 直径是最长的弦
B. 同圆中,所有的半径都相等
C. 圆既是轴对称图形又是中心对称图形
D. 长度相等的弧是等弧
课堂练习
D
解:A、直径是最长的弦,说法正确;
B、同圆中,所有的半径都相等,说法正确;
C、圆既是轴对称图形又是中心对称图形,说法正确;
D、在同圆或等圆中,长度相等的弧是等弧,原说法错误;
故选:D.
课堂练习
课堂练习
2.小明在半径为5的圆中测量弦AB的长度,下列测量结果中一定是错误的是( )
A. 4 B. 5 C. 10 D. 11
D
课堂练习
解:∵半径为5的圆,直径为10,
∴在半径为5的圆中测量弦AB的长度,
AB的取值范围是:0∴弦AB的长度可以是4,5,10,不可能为11.
故选:D.
课堂练习
3.下图是一个圆规,点A是铁尖的端点,点B是铅笔芯尖的端点,已知点A与点B的距离是2cm,若铁尖的端点A固定,铅笔芯尖的端点B绕点A旋转一周,则作出的圆中最长弦的长是 ( )
A. 1cm B. 2cm C. 4cm D. 5cm
C
课堂练习
解:由于AB是半径,为2cm,
所以直径是4cm,那么最大的弦是直径,
所以最长弦的长是4cm。
故选:C.
课堂总结
圆的对称性
圆既是轴对称图形
又是中心对称图形
圆的概念:半径,直径,弦,弧
圆心的距离(d)和半径(r)的关系
板书设计
2.1 圆的对称性
1.圆的概念
2.圆的对称性
中心对称
轴对称
3.圆心的距离(d)和半径(r)的关系
作业布置
必做题:课本习题 2.1的第1~3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.1圆的对称性
湘教版 九年级下
教学内容分析
在小学学习圆的基础上,进一步熟悉圆的概念,知道圆的半径、直径、弦、弧基本的概念,并且认识到圆既是轴对称图形,又是中心对称图形;本节还将学习点与圆的位置关系。本节的内容为后面的学习提供了基础知识。
教学目标
1.熟悉圆、圆心、半径、直径、弦、弧、等圆等概念;(重点)
2.知道圆是中心对称图形也是轴对称图形;
3.依据点到圆心的距离(d)和半径(r)的关系,判定点与圆的位置关系;掌握平面内的点与圆的位置关系及其条件.(重难点)
核心素养分析
本节内容是对几何图形--圆的认识,学生在本节内容学习到圆的概念,圆的对称性,以及圆心的距离(d)和半径(r)的关系,学生通过这些基础内容的认识,可以
培养几何直观的核心素养。
新知导入
同学们,你们在游乐场坐过摩天轮吗?它是什么形状呢?
圆
新知讲解
观察
在生活中, 我们经常看到圆的形象(如图 2-1)
图2-1
新知讲解
圆(circle)是平面内到一定点的距离等于定长的所有点组成的图形,
这个定点叫作圆心(center of a circle),
定长叫作半径(radius).
圆的静态定义
新知讲解
如图2-2,点O是圆心,圆心O与圆上一点的连线段叫作半径,线段OA是一条半径,
线段OA的长度也叫作半径,记作半径r.
以点O为圆心的圆叫作圆O,记作⊙O.
图2-2
注意:
1、确定圆的两个条件:圆心和半径,
圆心确定圆的位置,半径确定圆的大小;
2、圆指圆周,而非圆面.
新知讲解
新知讲解
动脑筋
圆也可以看成是平面内一个动点绕一个定点旋转一周所形成的图形(如图2-3),定点叫作圆心,定点与动点的连线段叫作半径。
o
圆的动态定义
图2-3
新知讲解
平面内的点与圆有什么位置关系呢?
我们把到圆心的距离小于半径的点叫作圆内的点; 到圆心的距离大于半径的点叫作圆外的点.
新知讲解
你能说出同一平面内的点与圆有几种位置关系? 怎样确定点与圆的位置关系? 请与同学交流.
新知讲解
一般地,设⊙O的半径为r,点P到圆心O的距离OP=d,
则有:
(1)点P在圆内 d<r;
(2)点P在圆上 d=r;
(3)点P在圆外 d>r.
●
O
●
●
●
P
P
C
P
r
新知讲解
圆的其他概念
连接圆上任意两点的线段叫作弦,经过圆心的弦叫作直径.
如图2-4,线段AB,CD是⊙O的弦,
弦AB经过圆心O,
因此线段AB是⊙O的直径。
O
D
C
A
B
·
图2-4
新知讲解
易错点:
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
新知讲解
圆上任意两点间的部分叫作圆弧,简称弧,弧用符号“︵” 表示。
如图2-5,⊙O上两点A,B间小于半圆的部分叫作劣弧, 记作 ;
A,B间大于半圆的部分叫作优弧 , 记作 ,
.
O
M
A
B
·
·
⌒
AB
⌒
AMB
图2-5
新知讲解
1. 如图2-6,在一块硬纸板和一张薄的白纸上分别画一个圆,使它们的半径相等,把白纸放在硬纸板上面, 使两个圆的圆心重合,观察这两个圆是否重合.
探究
图2-6
新知讲解
2.如图2-7,用一根大头针穿过上述两个圆的圆心.让硬纸板保持不动,让白纸绕圆心旋转任意角度.观察旋转后白纸上的圆是否仍然与硬纸板上的圆重合. 这体现圆具有什么样的性质?
图2-7
只有在同圆或等圆中才存在等弧,在大小不等的两个圆中不存在等弧。
在判断等弧时,首先要看两弧所在的圆是否为同圆或等圆,然后再看弧的长度是否相等.
新知讲解
我们把能够重合的两个圆叫作等圆,把能够互相重合的弧叫作等弧.
由于圆是由一个动点绕一个定点旋转一周所形成的图形,因此圆绕圆心旋转任意角度,都能与自身重合.
特别地,将圆绕圆心旋转180°时能与自身重合,所以,
新知讲解
圆是中心对称图形,圆心是它的对称中心
新知讲解
如图2-8,在纸上任画一个⊙O,并剪下来. 将⊙O沿任意一条直径(例如直径 CD)对折,你发现了什么?
说一说
直径CD两侧的两个半圆能完全重合。
图2-8
新知讲解
圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
新知讲解
易错点:
①圆的对称轴有无数条;
②因为直径是弦,弦是线段,而对称轴是直线,所以不能说“圆的对称轴是直径”,而应该说“圆的对称轴是直径所在的直线”.
新知讲解
如图2-9,为什么通常要把车轮设计成圆形?请说明理由.
议一议
图2-9
车轮做成圆形的主要原因是省力和平稳.
1.下列说法中,不正确的是( )
A. 直径是最长的弦
B. 同圆中,所有的半径都相等
C. 圆既是轴对称图形又是中心对称图形
D. 长度相等的弧是等弧
课堂练习
D
解:A、直径是最长的弦,说法正确;
B、同圆中,所有的半径都相等,说法正确;
C、圆既是轴对称图形又是中心对称图形,说法正确;
D、在同圆或等圆中,长度相等的弧是等弧,原说法错误;
故选:D.
课堂练习
课堂练习
2.小明在半径为5的圆中测量弦AB的长度,下列测量结果中一定是错误的是( )
A. 4 B. 5 C. 10 D. 11
D
课堂练习
解:∵半径为5的圆,直径为10,
∴在半径为5的圆中测量弦AB的长度,
AB的取值范围是:0
故选:D.
课堂练习
3.下图是一个圆规,点A是铁尖的端点,点B是铅笔芯尖的端点,已知点A与点B的距离是2cm,若铁尖的端点A固定,铅笔芯尖的端点B绕点A旋转一周,则作出的圆中最长弦的长是 ( )
A. 1cm B. 2cm C. 4cm D. 5cm
C
课堂练习
解:由于AB是半径,为2cm,
所以直径是4cm,那么最大的弦是直径,
所以最长弦的长是4cm。
故选:C.
课堂总结
圆的对称性
圆既是轴对称图形
又是中心对称图形
圆的概念:半径,直径,弦,弧
圆心的距离(d)和半径(r)的关系
板书设计
2.1 圆的对称性
1.圆的概念
2.圆的对称性
中心对称
轴对称
3.圆心的距离(d)和半径(r)的关系
作业布置
必做题:课本习题 2.1的第1~3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
