【核心素养目标】2.2.2圆周角(1)教学设计
文档属性
| 名称 | 【核心素养目标】2.2.2圆周角(1)教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 15:55:21 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教版版九年级下册数学 2.2.2圆周角(1)教学设计
课题 2.2.2圆周角(1) 单元 第一单元 学科 数学 年级 九
教材分析 本节在学习圆心角的基础上,推导出了圆周角定理;并得到了圆周角定理的推论.圆心角和圆周角的关系,本节还会学习运用圆周角定理及其推论来求解几何问题中圆周角和圆心角的大小。
核心素养分析 本主要认识圆周角定理和圆周角定理的推论,圆周角定理是圆周角与圆心角之间的数量关系,在圆的计算中是一个重要的定理,培养了学生的几何直观的核心素养,同时还培养了学生的计算能力。
学习目标 1.熟悉圆周角的概念,理解圆周角定理.2.探究圆周角与圆心角的关系,能运用圆周角定理解决简单的几何问题. 3.掌握并会运用圆周角定理的推论.
重点 探究圆周角与圆心角的关系,能运用圆周角定理解决简单的几何问题.
难点 掌握并会运用圆周角定理的推论.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 上节课我们学习了在同圆(或等圆)中,圆心角、弧、弦三个量之间关系是什么?在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等 回顾知识,温故知新,复习圆心角弧弦的之间的关系。 学生复习圆的知识,引入本节圆周角定理。
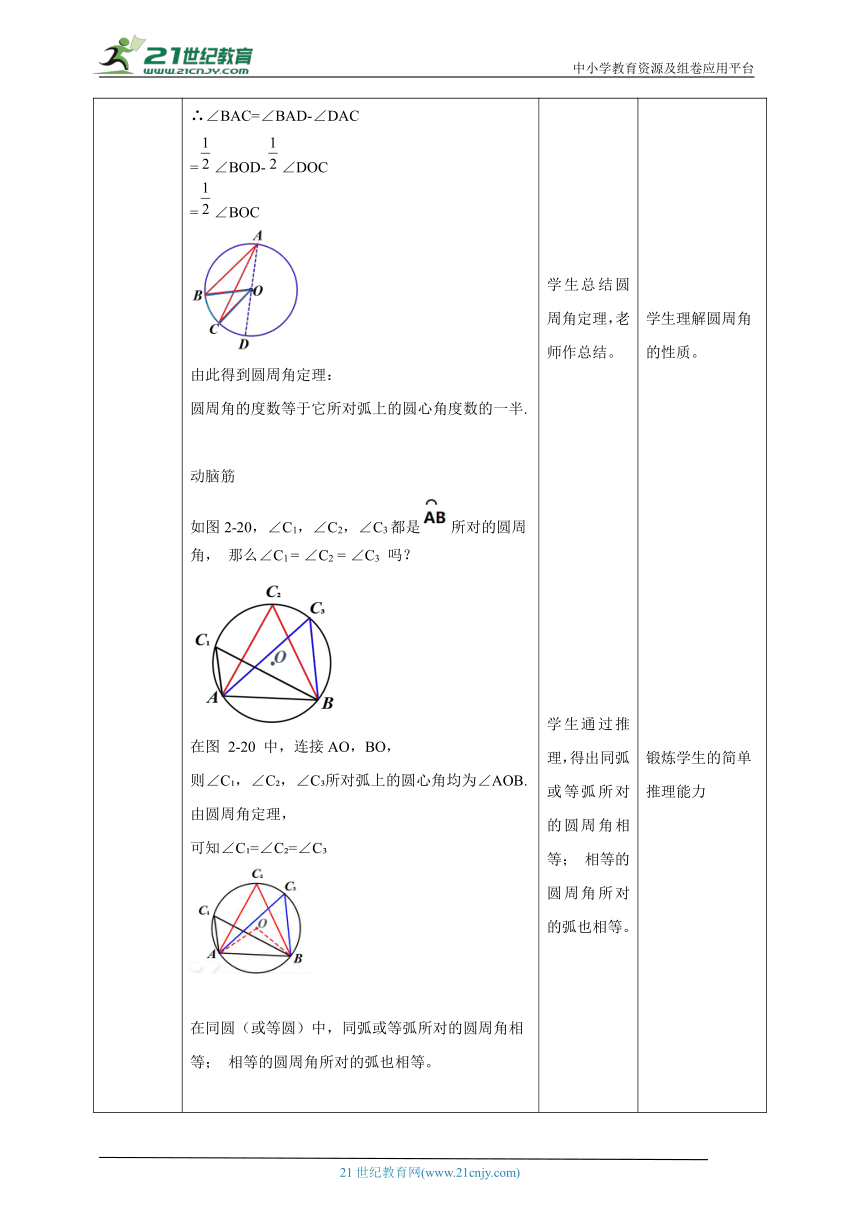
讲授新课 顶点A在圆上,它的两边都与圆相交,像这样的角叫作圆周角. 我们把∠BAC 叫作所对的圆周角,叫作圆周角∠BAC 所对的弧。同一条弧所对的圆周角只有一个吗?所对应的圆心角是∠BAC、∠BDC和∠BEC 同一条弧所对的圆周角有无数个.从共青团团旗上的图案抽象出如图2-16所示的图形,该图形中就有许多圆周角.探究分别测量图2-15 中所对的圆周角∠BAC和圆心角∠BOC的度数,它们之间有什么关系?请同学们任画一个圆,并在圆上任取一条弧,作出这条弧所对的圆周角和圆心角,测量出它们的度数. 你能得出同样的结论吗? 由此你能发现什么规律?通过度量, 我发现圆周角的度数等于它所对弧上的圆心角度数的一半.下面我们来证明这个结论.已知:在⊙O中,所对的圆周角是∠BAC,圆心角是∠BOC. 求证:∠BAC= ∠BOC. 圆周角与圆心角有几种不同的位置关系呢?在对于第(1)种情况, 如图2-17,圆心O在∠BAC的一边AB上. ∵ OA=OC, ∴ ∠C=∠BAC, ∴∠BOC=∠C+∠BAC=2∠BAC, 即∠BAC= ∠BOC.对于第(2)种情况, 如图2-18,圆心O在∠BAC的内部.作直径 AD, 根据第(1)种情况得∠BAD= ∠BOD, ∠DAC=∠DOC∴∠BAC=∠BAD+∠DAC =∠BOD+∠DOC =∠BOC对于第(3)种情况, 如图 2-19, 圆心 O 在∠BAC 的外部。请你完成∠BAC= ∠BOC 的证明 证明:∠BAD=∠BOD, ∠DAC=∠DOC∴∠BAC=∠BAD-∠DAC=∠BOD-∠DOC=∠BOC由此得到圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.动脑筋如图2-20,∠C1,∠C2,∠C3都是所对的圆周角, 那么∠C1 = ∠C2 = ∠C3 吗? 在图 2-20 中,连接AO,BO,则∠C ,∠C ,∠C 所对弧上的圆心角均为∠AOB.由圆周角定理,可知∠C =∠C =∠C 在同圆(或等圆)中,同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧也相等。例2 如图2-21,OA,OB,OC都是⊙O的半径,∠AOB=50°, ∠BOC =70°. 求∠ACB和∠BAC的度数解 ∵ 圆心角∠AOB与圆周角∠ACB所对的弧为, ∴ ∠ACB =∠AOB = 25°. 同理 ∠BAC =∠BOC = 35° 学生独立思考、小组合作,熟悉圆周角的概念。让学生观察实际生活中的圆周角。学生讨论圆周角与圆心角几种不同的位置关系 学生总结圆周角定理,老师作总结。 学生通过推理,得出同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧也相等。 理解圆周角的概念认识圆心角和圆周角的关系。学生理解圆周角的性质。 锻炼学生的简单推理能力
课堂练习 1.下图中各角是不是圆周角?请说明理由.解:如图(1),∠ABC的点B在⊙O上,两边与圆相交,则∠ABC为圆周角;如图(2),∠ABC的点B在⊙O上,两边与圆相交,则∠ABC为圆周角;如图(3),∠ABC的点B在⊙O外,则∠ABC不是圆周角;如图(4),∠ABC的点B在⊙O内,则∠ABC不是圆周角. 2.如图,点A、B、C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为___________ .解:如图,连接OB、OC∵∠BAC=30°,∴∠BOC=60°.∵OB=OC,∴△BOC是等边三角形,∴OB=BC=6.3.如图,点A,B,C在⊙O上,∠A=72°,求∠BOC和∠OBC的度数.解:∵∠BOC=2∠A,∠A=72°,∴∠BOC=144°,∵OB=OC,∴∠OBC=∠OCB=(180°-144°)÷2=18° 学生做练习,互相补充,有问题的地方教师进行订正 ,做最后总结,学生共同完成本节课练习。 练习是为了巩固学生圆周角的概念和性质。
课堂小结 学生先发言总结,在教师的引导下总结归纳圆周角的性质。 让学生自己对本节课知识进行整合归纳,培养学生养成及时总结的习惯,形成自己的知识体系。
板书 课题:2.2.2 圆周角1.圆周角定理2.圆周角定理的推论
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
湘教版版九年级下册数学 2.2.2圆周角(1)教学设计
课题 2.2.2圆周角(1) 单元 第一单元 学科 数学 年级 九
教材分析 本节在学习圆心角的基础上,推导出了圆周角定理;并得到了圆周角定理的推论.圆心角和圆周角的关系,本节还会学习运用圆周角定理及其推论来求解几何问题中圆周角和圆心角的大小。
核心素养分析 本主要认识圆周角定理和圆周角定理的推论,圆周角定理是圆周角与圆心角之间的数量关系,在圆的计算中是一个重要的定理,培养了学生的几何直观的核心素养,同时还培养了学生的计算能力。
学习目标 1.熟悉圆周角的概念,理解圆周角定理.2.探究圆周角与圆心角的关系,能运用圆周角定理解决简单的几何问题. 3.掌握并会运用圆周角定理的推论.
重点 探究圆周角与圆心角的关系,能运用圆周角定理解决简单的几何问题.
难点 掌握并会运用圆周角定理的推论.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 上节课我们学习了在同圆(或等圆)中,圆心角、弧、弦三个量之间关系是什么?在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等 回顾知识,温故知新,复习圆心角弧弦的之间的关系。 学生复习圆的知识,引入本节圆周角定理。
讲授新课 顶点A在圆上,它的两边都与圆相交,像这样的角叫作圆周角. 我们把∠BAC 叫作所对的圆周角,叫作圆周角∠BAC 所对的弧。同一条弧所对的圆周角只有一个吗?所对应的圆心角是∠BAC、∠BDC和∠BEC 同一条弧所对的圆周角有无数个.从共青团团旗上的图案抽象出如图2-16所示的图形,该图形中就有许多圆周角.探究分别测量图2-15 中所对的圆周角∠BAC和圆心角∠BOC的度数,它们之间有什么关系?请同学们任画一个圆,并在圆上任取一条弧,作出这条弧所对的圆周角和圆心角,测量出它们的度数. 你能得出同样的结论吗? 由此你能发现什么规律?通过度量, 我发现圆周角的度数等于它所对弧上的圆心角度数的一半.下面我们来证明这个结论.已知:在⊙O中,所对的圆周角是∠BAC,圆心角是∠BOC. 求证:∠BAC= ∠BOC. 圆周角与圆心角有几种不同的位置关系呢?在对于第(1)种情况, 如图2-17,圆心O在∠BAC的一边AB上. ∵ OA=OC, ∴ ∠C=∠BAC, ∴∠BOC=∠C+∠BAC=2∠BAC, 即∠BAC= ∠BOC.对于第(2)种情况, 如图2-18,圆心O在∠BAC的内部.作直径 AD, 根据第(1)种情况得∠BAD= ∠BOD, ∠DAC=∠DOC∴∠BAC=∠BAD+∠DAC =∠BOD+∠DOC =∠BOC对于第(3)种情况, 如图 2-19, 圆心 O 在∠BAC 的外部。请你完成∠BAC= ∠BOC 的证明 证明:∠BAD=∠BOD, ∠DAC=∠DOC∴∠BAC=∠BAD-∠DAC=∠BOD-∠DOC=∠BOC由此得到圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.动脑筋如图2-20,∠C1,∠C2,∠C3都是所对的圆周角, 那么∠C1 = ∠C2 = ∠C3 吗? 在图 2-20 中,连接AO,BO,则∠C ,∠C ,∠C 所对弧上的圆心角均为∠AOB.由圆周角定理,可知∠C =∠C =∠C 在同圆(或等圆)中,同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧也相等。例2 如图2-21,OA,OB,OC都是⊙O的半径,∠AOB=50°, ∠BOC =70°. 求∠ACB和∠BAC的度数解 ∵ 圆心角∠AOB与圆周角∠ACB所对的弧为, ∴ ∠ACB =∠AOB = 25°. 同理 ∠BAC =∠BOC = 35° 学生独立思考、小组合作,熟悉圆周角的概念。让学生观察实际生活中的圆周角。学生讨论圆周角与圆心角几种不同的位置关系 学生总结圆周角定理,老师作总结。 学生通过推理,得出同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧也相等。 理解圆周角的概念认识圆心角和圆周角的关系。学生理解圆周角的性质。 锻炼学生的简单推理能力
课堂练习 1.下图中各角是不是圆周角?请说明理由.解:如图(1),∠ABC的点B在⊙O上,两边与圆相交,则∠ABC为圆周角;如图(2),∠ABC的点B在⊙O上,两边与圆相交,则∠ABC为圆周角;如图(3),∠ABC的点B在⊙O外,则∠ABC不是圆周角;如图(4),∠ABC的点B在⊙O内,则∠ABC不是圆周角. 2.如图,点A、B、C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为___________ .解:如图,连接OB、OC∵∠BAC=30°,∴∠BOC=60°.∵OB=OC,∴△BOC是等边三角形,∴OB=BC=6.3.如图,点A,B,C在⊙O上,∠A=72°,求∠BOC和∠OBC的度数.解:∵∠BOC=2∠A,∠A=72°,∴∠BOC=144°,∵OB=OC,∴∠OBC=∠OCB=(180°-144°)÷2=18° 学生做练习,互相补充,有问题的地方教师进行订正 ,做最后总结,学生共同完成本节课练习。 练习是为了巩固学生圆周角的概念和性质。
课堂小结 学生先发言总结,在教师的引导下总结归纳圆周角的性质。 让学生自己对本节课知识进行整合归纳,培养学生养成及时总结的习惯,形成自己的知识体系。
板书 课题:2.2.2 圆周角1.圆周角定理2.圆周角定理的推论
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
