【新课标】2.2.2圆周角(1) 课件(共32张PPT)
文档属性
| 名称 | 【新课标】2.2.2圆周角(1) 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 16:00:28 | ||
图片预览








文档简介
(共32张PPT)
2.2.2圆周角(1)
湘教版 九年级下
教学内容分析
本节在学习圆心角的基础上,推导出了圆周角定理;并得到了圆周角定理的推论,圆心角和圆周角的关系,本节还会学习运用圆周角定理及其推论来求解几何问题中圆周角和圆心角的大小。
教学目标
1.熟悉圆周角的概念,理解圆周角定理.
2.探究圆周角与圆心角的关系,能运用圆周角定理解决简单的几何问题.(重难点)
3.掌握并会运用圆周角定理的推论.(难点)
核心素养分析
本节主要认识圆周角定理和圆周角定理的推论,圆周角定理是圆周角与圆心角之间的数量关系,在圆的计算中是一个重要的定理,培养了学生的几何直观的核心素养,同时还培养了学生的计算能力。
新知导入
上节课我们学习了在同圆(或等圆)中,圆心角、弧、弦三个量之间的关系是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
新知讲解
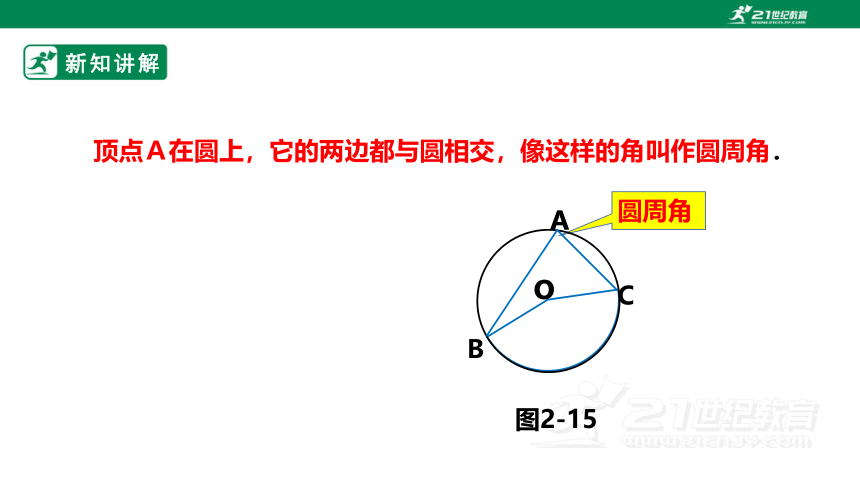
顶点A在圆上,它的两边都与圆相交,像这样的角叫作圆周角.
图2-15
B
C
A
O
A
O
圆周角
新知讲解
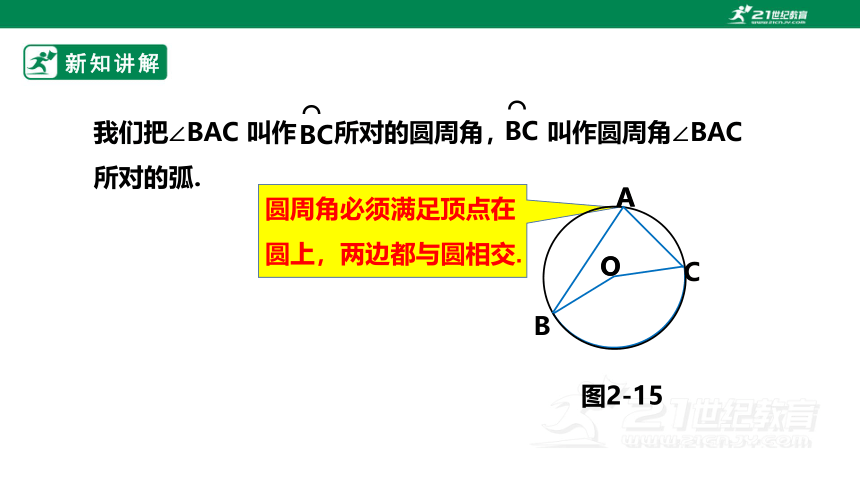
我们把∠BAC 叫作 所对的圆周角, 叫作圆周角∠BAC 所对的弧.
图2-15
⌒
BC
⌒
BC
B
C
A
O
A
O
圆周角必须满足顶点在圆上,两边都与圆相交.
新知讲解
图2-15
B
C
A
O
A
O
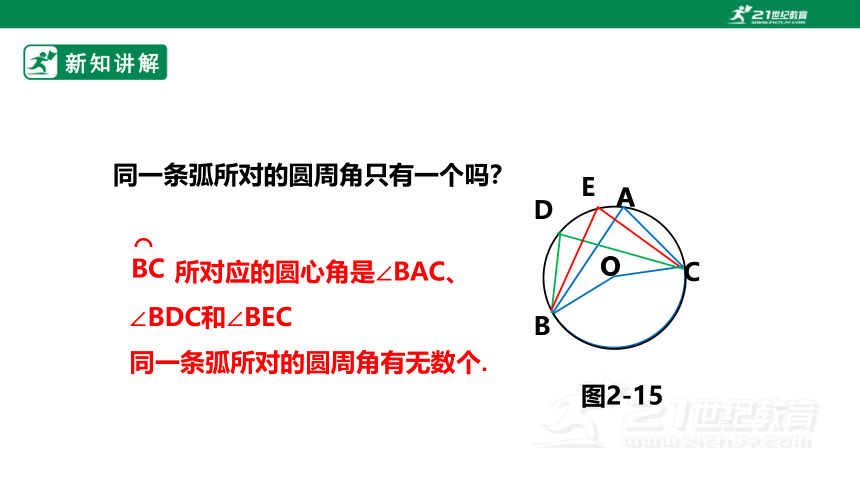
同一条弧所对的圆周角只有一个吗?
所对应的圆心角是∠BAC、∠BDC和∠BEC
同一条弧所对的圆周角有无数个.
E
D
⌒
BC
新知讲解
从共青团团旗上的图案抽象出如图2-16所示的图形,该图形中就有许多圆周角.
图2-16
新知讲解
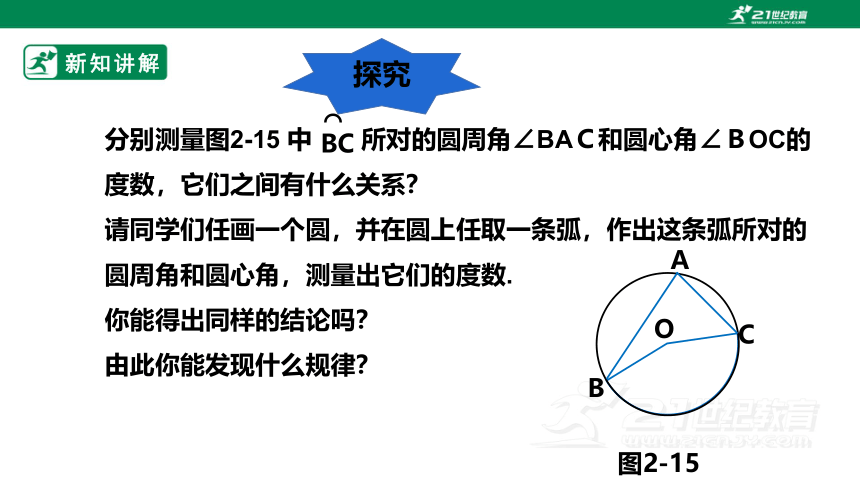
分别测量图2-15 中 所对的圆周角∠BAC和圆心角∠BOC的度数,它们之间有什么关系?
请同学们任画一个圆,并在圆上任取一条弧,作出这条弧所对的圆周角和圆心角,测量出它们的度数.
你能得出同样的结论吗?
由此你能发现什么规律?
图2-15
探究
B
C
A
O
⌒
BC
新知讲解
通过度量, 发现圆周角的度数等于它所对弧上的圆心角度数的一半.
新知讲解
下面我们来证明这个结论.
已知:在⊙O中, 所对的圆周角是∠BAC,圆心角是
∠BOC.
求证:∠BAC= ∠BOC.
⌒
BC
圆周角与圆心角有几种不同的位置关系呢?
新知讲解
圆周角的一边通过圆心
圆心在圆周角的内部
圆心在圆周角的外部
新知讲解
在对于第(1)种情况, 如图2-17,圆心O在∠BAC的一边AB上.
∵ OA=OC,
∴ ∠C=∠BAC,
∴∠BOC=∠C+∠BAC=2∠BAC,
即∠BAC= ∠BOC.
图2-17
新知讲解
对于第(2)种情况, 如图2-18,圆心O在∠BAC的内部.
作直径 AD, 根据第(1)种情况得
∠BAD= ∠BOD, ∠DAC= ∠DOC
∴∠BAC=∠BAD+∠DAC
= ∠BOD+ ∠DOC
= ∠BOC
图2-18
新知讲解
对于第(3)种情况, 如图 2-19, 圆心 O 在∠BAC 的外部。
请你完成∠BAC= ∠BOC 的证明
图2-19
证明:∠BAD= ∠BOD, ∠DAC= ∠DOC
∴∠BAC=∠BAD-∠DAC
= ∠BOD- ∠DOC
= ∠BOC
新知讲解
由此得到圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
新知讲解
如图2-20,∠C1,∠C2,∠C3都是 所对的圆周角, 那么∠C1 = ∠C2 = ∠C3 吗?
动脑筋
图2-20
⌒
AB
新知讲解
在图 2-20 中,
连接AO,BO,
则∠C ,∠C ,∠C 所对弧上的圆心角均为∠AOB.
由圆周角定理,
可知∠C =∠C =∠C .
-------
------
图 2-20
新知讲解
在同圆(或等圆)中,同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧也相等。
新知讲解
例2 如图2-21,OA,OB,OC都是⊙O的半径,∠AOB=50°, ∠BOC =70°. 求∠ACB和∠BAC的度数.
图2-21
解 ∵ 圆心角∠AOB与圆周角∠ACB所对的弧为 ,
∴ ∠ACB = ∠AOB = 25°.
同理 ∠BAC = ∠BOC = 35°
A
O
B
C
50°
70°
⌒
AB
1.下图中各角是不是圆周角?请说明理由.
课堂练习
课堂练习
解:如图(1),∠ABC的点B在⊙O上,两边与圆相交,则∠ABC为圆周角;
如图(2),∠ABC的点B在⊙O上,两边与圆相交,则∠ABC为圆周角;
如图(3),∠ABC的点B在⊙O外,则∠ABC不是圆周角;
如图(4),∠ABC的点B在⊙O内,则∠ABC不是圆周角.
课堂练习
2.如图,点A、B、C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为___________ .
6
课堂练习
解:如图,连接OB、OC
∵∠BAC=30°,
∴∠BOC=60°.
∵OB=OC,
∴△BOC是等边三角形,
∴OB=BC=6.
课堂练习
3.如图,点A,B,C在⊙O上,∠A=72°,求∠BOC和∠OBC的度数.
课堂练习
解:
∵∠BOC=2∠A,∠A=72°,
∴∠BOC=144°,
∵OB=OC,
∴∠OBC=∠OCB=(180°-144°)÷2=18°.
课堂总结
圆周角
圆周角定理的推论
圆周角定理
板书设计
2.2.2 圆周角
1.圆周角定理
2. 圆周角定理的推论
作业布置
必做题:课本52页的练习第2,3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.2.2圆周角(1)
湘教版 九年级下
教学内容分析
本节在学习圆心角的基础上,推导出了圆周角定理;并得到了圆周角定理的推论,圆心角和圆周角的关系,本节还会学习运用圆周角定理及其推论来求解几何问题中圆周角和圆心角的大小。
教学目标
1.熟悉圆周角的概念,理解圆周角定理.
2.探究圆周角与圆心角的关系,能运用圆周角定理解决简单的几何问题.(重难点)
3.掌握并会运用圆周角定理的推论.(难点)
核心素养分析
本节主要认识圆周角定理和圆周角定理的推论,圆周角定理是圆周角与圆心角之间的数量关系,在圆的计算中是一个重要的定理,培养了学生的几何直观的核心素养,同时还培养了学生的计算能力。
新知导入
上节课我们学习了在同圆(或等圆)中,圆心角、弧、弦三个量之间的关系是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
新知讲解
顶点A在圆上,它的两边都与圆相交,像这样的角叫作圆周角.
图2-15
B
C
A
O
A
O
圆周角
新知讲解
我们把∠BAC 叫作 所对的圆周角, 叫作圆周角∠BAC 所对的弧.
图2-15
⌒
BC
⌒
BC
B
C
A
O
A
O
圆周角必须满足顶点在圆上,两边都与圆相交.
新知讲解
图2-15
B
C
A
O
A
O
同一条弧所对的圆周角只有一个吗?
所对应的圆心角是∠BAC、∠BDC和∠BEC
同一条弧所对的圆周角有无数个.
E
D
⌒
BC
新知讲解
从共青团团旗上的图案抽象出如图2-16所示的图形,该图形中就有许多圆周角.
图2-16
新知讲解
分别测量图2-15 中 所对的圆周角∠BAC和圆心角∠BOC的度数,它们之间有什么关系?
请同学们任画一个圆,并在圆上任取一条弧,作出这条弧所对的圆周角和圆心角,测量出它们的度数.
你能得出同样的结论吗?
由此你能发现什么规律?
图2-15
探究
B
C
A
O
⌒
BC
新知讲解
通过度量, 发现圆周角的度数等于它所对弧上的圆心角度数的一半.
新知讲解
下面我们来证明这个结论.
已知:在⊙O中, 所对的圆周角是∠BAC,圆心角是
∠BOC.
求证:∠BAC= ∠BOC.
⌒
BC
圆周角与圆心角有几种不同的位置关系呢?
新知讲解
圆周角的一边通过圆心
圆心在圆周角的内部
圆心在圆周角的外部
新知讲解
在对于第(1)种情况, 如图2-17,圆心O在∠BAC的一边AB上.
∵ OA=OC,
∴ ∠C=∠BAC,
∴∠BOC=∠C+∠BAC=2∠BAC,
即∠BAC= ∠BOC.
图2-17
新知讲解
对于第(2)种情况, 如图2-18,圆心O在∠BAC的内部.
作直径 AD, 根据第(1)种情况得
∠BAD= ∠BOD, ∠DAC= ∠DOC
∴∠BAC=∠BAD+∠DAC
= ∠BOD+ ∠DOC
= ∠BOC
图2-18
新知讲解
对于第(3)种情况, 如图 2-19, 圆心 O 在∠BAC 的外部。
请你完成∠BAC= ∠BOC 的证明
图2-19
证明:∠BAD= ∠BOD, ∠DAC= ∠DOC
∴∠BAC=∠BAD-∠DAC
= ∠BOD- ∠DOC
= ∠BOC
新知讲解
由此得到圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
新知讲解
如图2-20,∠C1,∠C2,∠C3都是 所对的圆周角, 那么∠C1 = ∠C2 = ∠C3 吗?
动脑筋
图2-20
⌒
AB
新知讲解
在图 2-20 中,
连接AO,BO,
则∠C ,∠C ,∠C 所对弧上的圆心角均为∠AOB.
由圆周角定理,
可知∠C =∠C =∠C .
-------
------
图 2-20
新知讲解
在同圆(或等圆)中,同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧也相等。
新知讲解
例2 如图2-21,OA,OB,OC都是⊙O的半径,∠AOB=50°, ∠BOC =70°. 求∠ACB和∠BAC的度数.
图2-21
解 ∵ 圆心角∠AOB与圆周角∠ACB所对的弧为 ,
∴ ∠ACB = ∠AOB = 25°.
同理 ∠BAC = ∠BOC = 35°
A
O
B
C
50°
70°
⌒
AB
1.下图中各角是不是圆周角?请说明理由.
课堂练习
课堂练习
解:如图(1),∠ABC的点B在⊙O上,两边与圆相交,则∠ABC为圆周角;
如图(2),∠ABC的点B在⊙O上,两边与圆相交,则∠ABC为圆周角;
如图(3),∠ABC的点B在⊙O外,则∠ABC不是圆周角;
如图(4),∠ABC的点B在⊙O内,则∠ABC不是圆周角.
课堂练习
2.如图,点A、B、C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为___________ .
6
课堂练习
解:如图,连接OB、OC
∵∠BAC=30°,
∴∠BOC=60°.
∵OB=OC,
∴△BOC是等边三角形,
∴OB=BC=6.
课堂练习
3.如图,点A,B,C在⊙O上,∠A=72°,求∠BOC和∠OBC的度数.
课堂练习
解:
∵∠BOC=2∠A,∠A=72°,
∴∠BOC=144°,
∵OB=OC,
∴∠OBC=∠OCB=(180°-144°)÷2=18°.
课堂总结
圆周角
圆周角定理的推论
圆周角定理
板书设计
2.2.2 圆周角
1.圆周角定理
2. 圆周角定理的推论
作业布置
必做题:课本52页的练习第2,3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
