【新课标】2.2.2圆周角(2) 课件(共37张PPT)
文档属性
| 名称 | 【新课标】2.2.2圆周角(2) 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 16:03:50 | ||
图片预览











文档简介
(共37张PPT)
2.2.2圆周角(2)
湘教版 九年级下
教学内容分析
在上节学习圆周角的基础上,本节课将继续学习圆周角,主要有2个内容,一是“直径所对的圆周角是直角,90°的圆周角所对的弦是直径”;二是理解圆内接四边形的概念,得出“圆内接四边形的对角互补”这个结论,学生本节课继续学习圆周角的结论,并进行圆周角的计算。
教学目标
1.掌握“直径所对的圆周角是直角,90°的圆周角所对的弦是直径”(重点)
2.理解圆内接四边形、四边形的外接圆等概念(难点)
3.理解“圆内接四边形的对角互补”的结论,并会计算。
核心素养分析
本节学习的内容,一是特殊的圆周角,“直径所对的圆周角是直角,90°的圆周角所对的弦是直径”;二是圆内接四边形的对角互补,对角也就是圆周角,这些知识点在圆周角的计算中比较重要,培养了学生的几何直观的核心素养,同时还培养了学生的观察和计算能力。
新知导入
圆周角定理是什么?圆周角定理的推论是什么?
圆周角的度数等于它所对弧上的圆心角度数的一半.
在同圆(或等圆)中,同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧也相等。
新知讲解
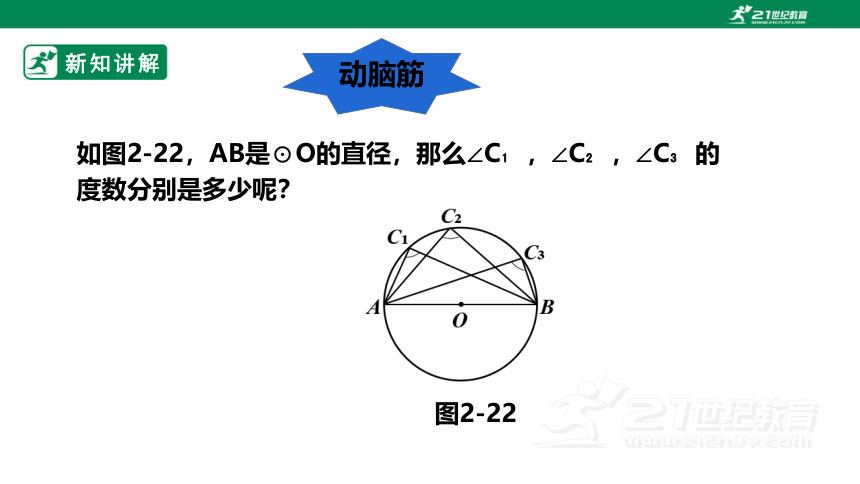
如图2-22,AB是⊙O的直径,那么∠C ,∠C ,∠C 的度数分别是多少呢?
图2-22
动脑筋
新知讲解
证明:∵∠C ,∠C ,∠C 所对的圆心角是∠AOB,
又∵A,O,B在一条直线上,
∴圆心角∠AOB是一个平角,即∠AOB=180°,
根据圆周角定理
故∠C =∠C =∠C = ×180°=90°
即直径所对的圆周角是直角。
新知讲解
若已知∠C1 = 90°, 它所对的弦AB是直径吗?
图2-22
证明:∵∠C 所对的圆心角是∠AOB
又∵∠C1 = 90°
∴∠AOB=180°
∴A、O、B三点共线
∵O是圆心
∴AB是直径
新知讲解
直径所对的圆周角是直角
A
B
O
C
AB是圆的直径,
∠ACB是AB所对的圆周角
∠ACB是直角
几何语言:
新知讲解
90°的圆周角所对的弦是直径.
A
B
O
C
∠ACB是AB所对的圆周角且∠ACB=90°
AB是直径
几何语言:
新知讲解
判断下列说法是否正确:
(1)在同圆或等圆中,等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆心角也相等 ( )
(3)90°的角所对的弦是直径 ( )
(4)等弧所对的圆周角相等 ( )
√
×
×
×
新知讲解
例3 如图,BC都是⊙O的直径,∠ABC=60°, 点D在⊙O上.求∠ADB的度数.
分析:由BC是⊙O的直径,得∠BAC=90°,再根据同弧所对的圆周角相等进行计算。
新知讲解
解: ∵BC为直径,
∴∠BAC = 90°.
又∠ABC = 60°,
∴ ∠ACB = 30°.
又∵∠ADB 与∠ACB 都是 所对的圆周角,
∴ ∠ADB = ∠ACB= 30°.
新知讲解
变式1 如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为( )
A. 57° B. 52° C. 38° D. 26°
解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=38°,
∴∠BAC=90°-∠ABC=52°,
∴∠BDC=∠BAC=52°.
B
新知讲解
图2-24
A
B
D
C
.O
这个圆叫作这个四边形的外接圆
我们把四边形ABCD叫作圆内接四边形
新知讲解
在图 2-24的四边形 ABCD 中, 两组对角∠A与∠C, ∠B与∠D有什么关系?
动脑筋
图2-24
A
B
D
C
.O
新知讲解
解:连接OB,OD,
∵ ∠A所对的弧为 ,∠C都是所对的弧为 ,
又 与 所对的圆心角之和是周角,
∠A+∠C=360°÷2=180°
由四边形内角和定理可知,
∠ABC+∠ADC=180°.
图2-25
⌒
BAD
⌒
BCD
⌒
BCD
⌒
BAD
.O
A
B
D
C
-----------
----------
.O
新知讲解
圆内接四边形的对角互补
.O
A
B
D
C
几何语言:
∵四边形ABCD是圆内接四边形
∴∠ABC+∠ADC=180°,
∠BAD+∠BCD=180°
新知讲解
例4 如图2-26,四边形ABCD为⊙O的内接四边形,已知∠BOD 为100°,求∠BAD及∠BCD的度数。
图2-26
新知讲解
解∵ 圆心角∠BOD与圆周角∠BAD 所对的弧为, ∠BOD = 100°,
∴ ∠BAD = ∠BOD = ×100° = 50°.
∵ ∠BCD + ∠BAD = 180°,
∴ ∠BCD = 180°-∠BAD=180°-50°=130°.
图2-26
新知讲解
变式2 如图,AB是半圆O的直径,∠BAC=20°,则∠D的度数是( )
A. 115° B. 110° C. 120° D. 135°
B
新知讲解
解:如图,连接BC,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°,
∵∠BAC=20°,
∴∠ABC=90°-20°=70°,
∵圆内接四边形的对角互补,
∴∠D+∠ABC=180°,
∴∠D=180°-70°=110°
变式3 如图,圆内接四边形ABCD的外角∠DCE =85°,求∠A的度数.
新知讲解
新知讲解
解: ∵四边形ABCD是圆内接四边形,
∴∠A = 180°-∠BCD
= ∠DCE =85°.
任一外角与其相邻的内角的对角相等
新知讲解
圆内接四边形小结(如图):
(1)对角互补:∠A + ∠BCD =180°,∠B +∠D = 180°.
(2)四个角的和是 360°:∠A +∠B +∠BCD +∠D =360°.
(3)圆内接四边形的外角等于其内对角:∠A=∠DCE
课堂练习
1. 如图,四边形ABCD内接于⊙O,若∠C=100°,则∠A的度数是( )
A. 80° B. 100° C. 110° D. 120°
A
课堂练习
解:∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∵∠C=100°,
∴∠A=180°-∠C=180°-100°=80°,
故选:A.
2.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A. 100° B. 110° C. 120° D. 130°.
课堂练习
C
课堂练习
解:∵四边形ABCD是⊙O的内接四边形,
∴∠A=180°-∠BCD=60°,
由圆周角定理得,
∠BOD=2∠A=120°,
故选:C.
课堂练习
3. 如图,点A,B,C,D四点均在⊙O上,∠AOD=68°,AO//DC,则∠B的度数为______.
56°
课堂练习
解:连接AD,
∵∠AOD=68°,
AO//DC,
∴∠ODC=∠AOD=68°,
∵∠AOD=68°,OA=OD,
课堂练习
解:∴∠OAD=∠ODA=(180°-∠AOD)÷2=56°,
∴∠ADC=∠ODA+∠ODC=56°+68°=124°,
∵四边形ABCD是⊙O的内接四边形,
∴∠B+∠ADC=180°,
∴∠B=56°.
课堂总结
圆周角
2圆内接四边形的对角互补.
1直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.
板书设计
2.2.2 圆周角(2)
1.直径所对的圆周角
2.圆内接四边形定义、性质
作业布置
必做题:课本55页的练习第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.2.2圆周角(2)
湘教版 九年级下
教学内容分析
在上节学习圆周角的基础上,本节课将继续学习圆周角,主要有2个内容,一是“直径所对的圆周角是直角,90°的圆周角所对的弦是直径”;二是理解圆内接四边形的概念,得出“圆内接四边形的对角互补”这个结论,学生本节课继续学习圆周角的结论,并进行圆周角的计算。
教学目标
1.掌握“直径所对的圆周角是直角,90°的圆周角所对的弦是直径”(重点)
2.理解圆内接四边形、四边形的外接圆等概念(难点)
3.理解“圆内接四边形的对角互补”的结论,并会计算。
核心素养分析
本节学习的内容,一是特殊的圆周角,“直径所对的圆周角是直角,90°的圆周角所对的弦是直径”;二是圆内接四边形的对角互补,对角也就是圆周角,这些知识点在圆周角的计算中比较重要,培养了学生的几何直观的核心素养,同时还培养了学生的观察和计算能力。
新知导入
圆周角定理是什么?圆周角定理的推论是什么?
圆周角的度数等于它所对弧上的圆心角度数的一半.
在同圆(或等圆)中,同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧也相等。
新知讲解
如图2-22,AB是⊙O的直径,那么∠C ,∠C ,∠C 的度数分别是多少呢?
图2-22
动脑筋
新知讲解
证明:∵∠C ,∠C ,∠C 所对的圆心角是∠AOB,
又∵A,O,B在一条直线上,
∴圆心角∠AOB是一个平角,即∠AOB=180°,
根据圆周角定理
故∠C =∠C =∠C = ×180°=90°
即直径所对的圆周角是直角。
新知讲解
若已知∠C1 = 90°, 它所对的弦AB是直径吗?
图2-22
证明:∵∠C 所对的圆心角是∠AOB
又∵∠C1 = 90°
∴∠AOB=180°
∴A、O、B三点共线
∵O是圆心
∴AB是直径
新知讲解
直径所对的圆周角是直角
A
B
O
C
AB是圆的直径,
∠ACB是AB所对的圆周角
∠ACB是直角
几何语言:
新知讲解
90°的圆周角所对的弦是直径.
A
B
O
C
∠ACB是AB所对的圆周角且∠ACB=90°
AB是直径
几何语言:
新知讲解
判断下列说法是否正确:
(1)在同圆或等圆中,等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆心角也相等 ( )
(3)90°的角所对的弦是直径 ( )
(4)等弧所对的圆周角相等 ( )
√
×
×
×
新知讲解
例3 如图,BC都是⊙O的直径,∠ABC=60°, 点D在⊙O上.求∠ADB的度数.
分析:由BC是⊙O的直径,得∠BAC=90°,再根据同弧所对的圆周角相等进行计算。
新知讲解
解: ∵BC为直径,
∴∠BAC = 90°.
又∠ABC = 60°,
∴ ∠ACB = 30°.
又∵∠ADB 与∠ACB 都是 所对的圆周角,
∴ ∠ADB = ∠ACB= 30°.
新知讲解
变式1 如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为( )
A. 57° B. 52° C. 38° D. 26°
解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=38°,
∴∠BAC=90°-∠ABC=52°,
∴∠BDC=∠BAC=52°.
B
新知讲解
图2-24
A
B
D
C
.O
这个圆叫作这个四边形的外接圆
我们把四边形ABCD叫作圆内接四边形
新知讲解
在图 2-24的四边形 ABCD 中, 两组对角∠A与∠C, ∠B与∠D有什么关系?
动脑筋
图2-24
A
B
D
C
.O
新知讲解
解:连接OB,OD,
∵ ∠A所对的弧为 ,∠C都是所对的弧为 ,
又 与 所对的圆心角之和是周角,
∠A+∠C=360°÷2=180°
由四边形内角和定理可知,
∠ABC+∠ADC=180°.
图2-25
⌒
BAD
⌒
BCD
⌒
BCD
⌒
BAD
.O
A
B
D
C
-----------
----------
.O
新知讲解
圆内接四边形的对角互补
.O
A
B
D
C
几何语言:
∵四边形ABCD是圆内接四边形
∴∠ABC+∠ADC=180°,
∠BAD+∠BCD=180°
新知讲解
例4 如图2-26,四边形ABCD为⊙O的内接四边形,已知∠BOD 为100°,求∠BAD及∠BCD的度数。
图2-26
新知讲解
解∵ 圆心角∠BOD与圆周角∠BAD 所对的弧为, ∠BOD = 100°,
∴ ∠BAD = ∠BOD = ×100° = 50°.
∵ ∠BCD + ∠BAD = 180°,
∴ ∠BCD = 180°-∠BAD=180°-50°=130°.
图2-26
新知讲解
变式2 如图,AB是半圆O的直径,∠BAC=20°,则∠D的度数是( )
A. 115° B. 110° C. 120° D. 135°
B
新知讲解
解:如图,连接BC,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°,
∵∠BAC=20°,
∴∠ABC=90°-20°=70°,
∵圆内接四边形的对角互补,
∴∠D+∠ABC=180°,
∴∠D=180°-70°=110°
变式3 如图,圆内接四边形ABCD的外角∠DCE =85°,求∠A的度数.
新知讲解
新知讲解
解: ∵四边形ABCD是圆内接四边形,
∴∠A = 180°-∠BCD
= ∠DCE =85°.
任一外角与其相邻的内角的对角相等
新知讲解
圆内接四边形小结(如图):
(1)对角互补:∠A + ∠BCD =180°,∠B +∠D = 180°.
(2)四个角的和是 360°:∠A +∠B +∠BCD +∠D =360°.
(3)圆内接四边形的外角等于其内对角:∠A=∠DCE
课堂练习
1. 如图,四边形ABCD内接于⊙O,若∠C=100°,则∠A的度数是( )
A. 80° B. 100° C. 110° D. 120°
A
课堂练习
解:∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∵∠C=100°,
∴∠A=180°-∠C=180°-100°=80°,
故选:A.
2.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A. 100° B. 110° C. 120° D. 130°.
课堂练习
C
课堂练习
解:∵四边形ABCD是⊙O的内接四边形,
∴∠A=180°-∠BCD=60°,
由圆周角定理得,
∠BOD=2∠A=120°,
故选:C.
课堂练习
3. 如图,点A,B,C,D四点均在⊙O上,∠AOD=68°,AO//DC,则∠B的度数为______.
56°
课堂练习
解:连接AD,
∵∠AOD=68°,
AO//DC,
∴∠ODC=∠AOD=68°,
∵∠AOD=68°,OA=OD,
课堂练习
解:∴∠OAD=∠ODA=(180°-∠AOD)÷2=56°,
∴∠ADC=∠ODA+∠ODC=56°+68°=124°,
∵四边形ABCD是⊙O的内接四边形,
∴∠B+∠ADC=180°,
∴∠B=56°.
课堂总结
圆周角
2圆内接四边形的对角互补.
1直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.
板书设计
2.2.2 圆周角(2)
1.直径所对的圆周角
2.圆内接四边形定义、性质
作业布置
必做题:课本55页的练习第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
