24.1旋转(1) 课件(共25张PPT)
文档属性
| 名称 | 24.1旋转(1) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
沪科版 九年级下册
24.1图形的旋转(1)
教学目标:
1.通过观察具体实例学习旋转概念,会画一个图形
作旋转后所得的图形;
2.探究旋转的性质,并在观察、猜想、验证、归纳、
概括的探究过程中,发展合情推理能力,进一步
体会图形运动中的变和不变.
教学重点:
旋转的性质.
课件说明
一、引入:
生活中,旋转的现象普遍存在。如:
一、引入:
生活中,旋转的现象普遍存在。如:
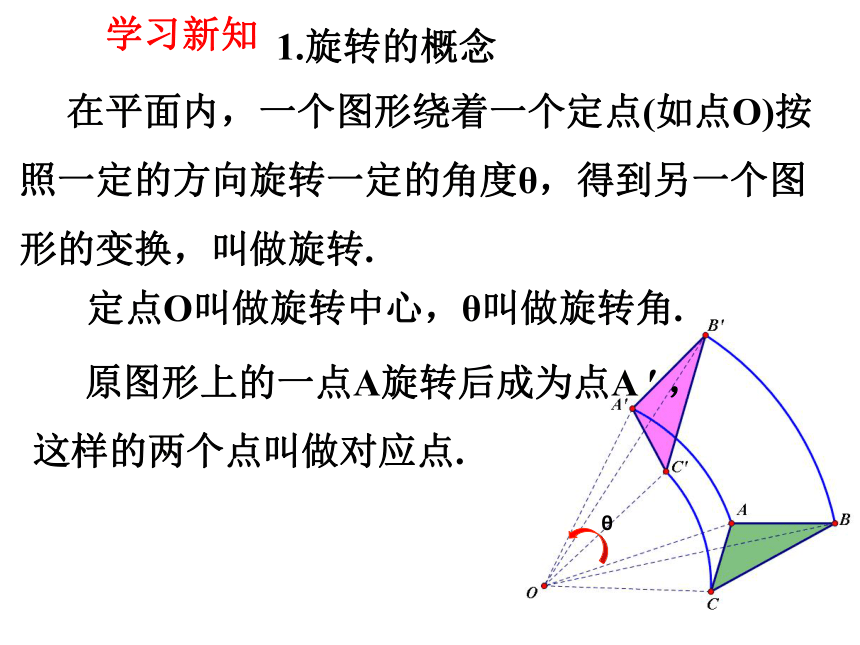
1.旋转的概念
在平面内,一个图形绕着一个定点(如点O)按照一定的方向旋转一定的角度θ,得到另一个图形的变换,叫做旋转.
定点O叫做旋转中心,θ叫做旋转角.
原图形上的一点A旋转后成为点A ′ ,
这样的两个点叫做对应点.
θ
学习新知
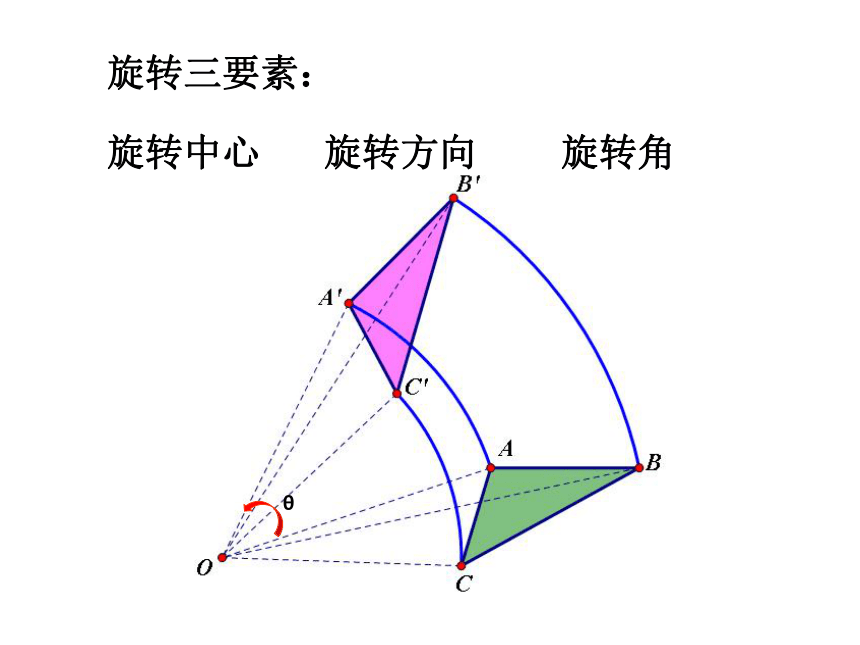
旋转三要素:
旋转中心
旋转方向
旋转角
θ
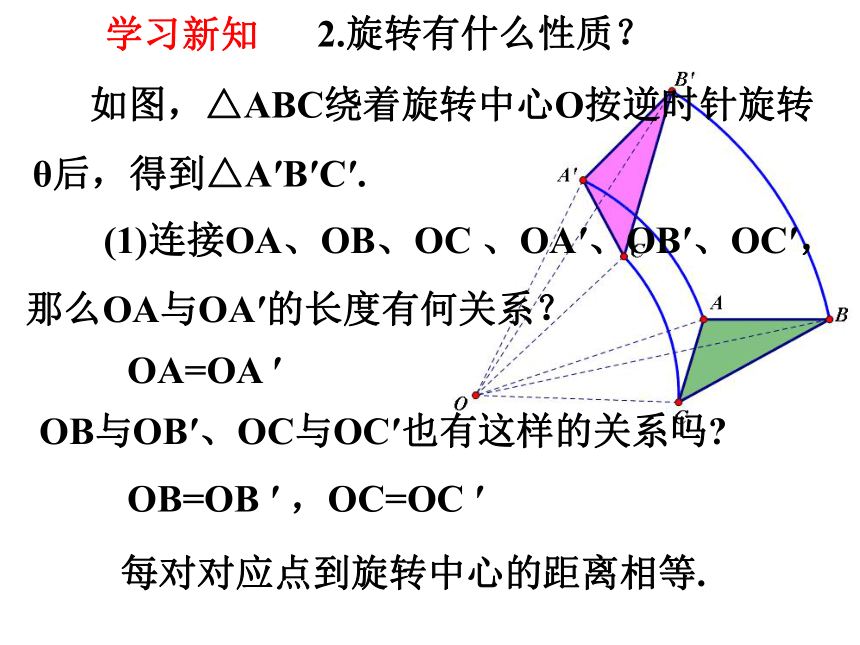
如图,△ABC绕着旋转中心O按逆时针旋转θ后,得到△A′B′C′.
2.旋转有什么性质?
(1)连接OA、OB、OC 、OA′、OB′、OC′,那么OA与OA′的长度有何关系?
OB与OB′、OC与OC′也有这样的关系吗
OA=OA ′
OB=OB ′ ,OC=OC ′
每对对应点到旋转中心的距离相等.
学习新知
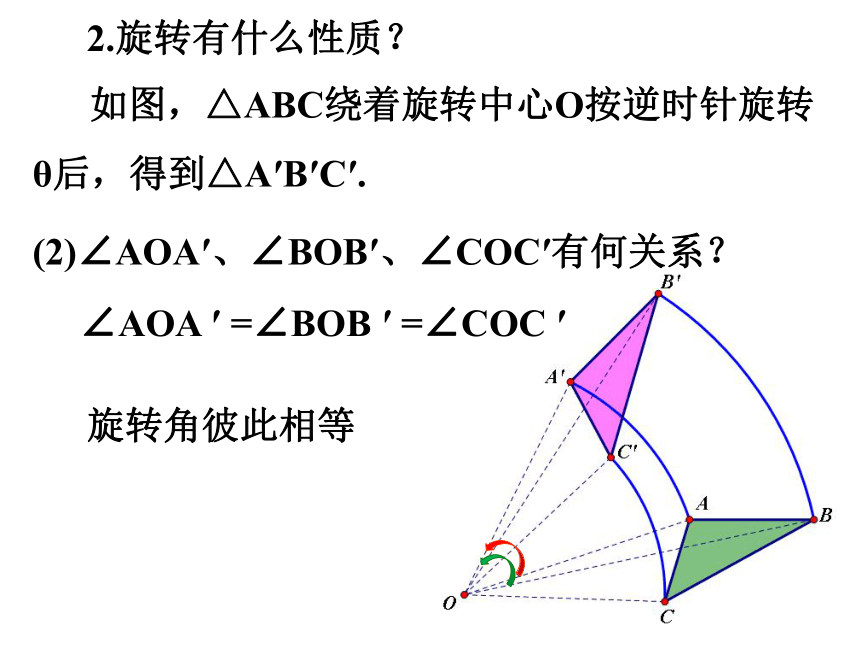
如图,△ABC绕着旋转中心O按逆时针旋转θ后,得到△A′B′C′.
(2)∠AOA′、∠BOB′、∠COC′有何关系?
2.旋转有什么性质?
∠AOA ′ =∠BOB ′ =∠COC ′
旋转角彼此相等
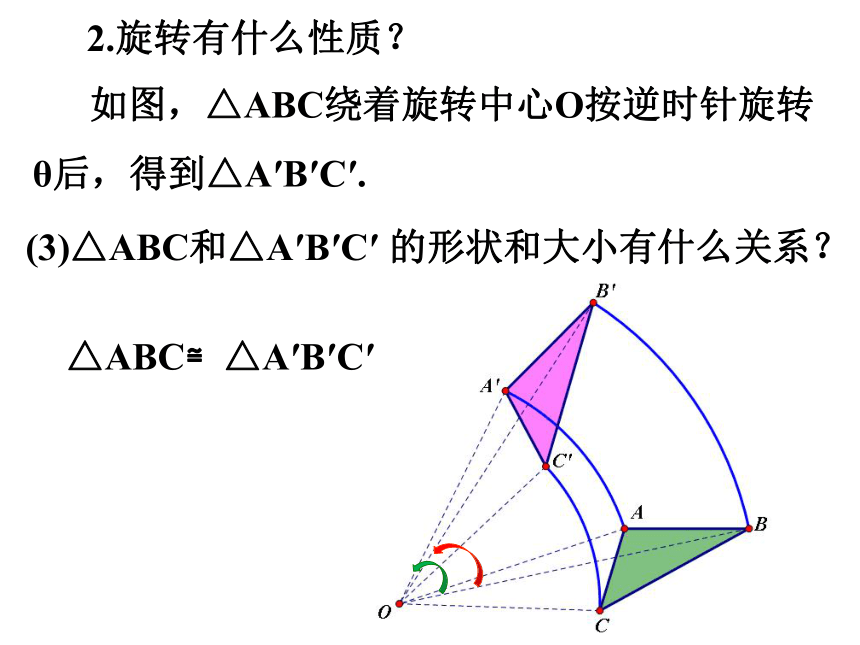
如图,△ABC绕着旋转中心O按逆时针旋转θ后,得到△A′B′C′.
2.旋转有什么性质?
(3)△ABC和△A′B′C′ 的形状和大小有什么关系?
△ABC≌△A′B′C′
2.旋转的性质:
一个图形和它经过旋转所得到的图形中,
(1)对应点到旋转中心的距离相等;
(2)两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
(3)旋转中心是唯一不动的点.
(4)旋转前后的两个图形是全等形.
在平面内,一个图形绕着一个定点旋转一定角度后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心.
如□ ABCD绕着一个定点O旋转180°能够与原图形重合.
平行四边形是旋转对称图形,
定点O就是旋转中心.
O
A
B
C
D
学习新知
在平面内,一个图形绕着一个定点旋转一定角度后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心.
如图绕着定点O旋转120°或240°能够与原图形重合.
O
旋转180°
1.找出下列旋转对称图形的旋转中心,并指出这个图形至少要旋转多大角度才能与原图形重合.
练习巩固
旋转72°
2.找出下列旋转对称图形的旋转中心,并指出这个图形至少要旋转多大角度才能与原图形重合.
O
72°
3.找出下列旋转对称图形的旋转中心,并指出这个图形至少要旋转多大角度才能与原图形重合.
旋转60°
60°
4.在下列图形中:
(1)指出轴对称图形,并用虚线画出该图形的对称轴(2)指出旋转对称图形,用“ ”号标出该图形的旋转中心, 并指出这个图形至少要旋转多大角度才能与原图形重合.
(1)如何画出旋转后的图形?
(2)如何确定旋转后的对应点的位置?
1.确定旋转中心;
2.确定旋转方向;
3.确定旋转角.
1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连线段的夹角等于旋转角.
课堂小结
(3)对比平移、轴对称,旋转的性质,它们有哪些
相同点和不同点?
1.如图,将△AOB绕点O按逆时针方向旋转45°
得到△A ′ OB ′.若∠AOB=21°,则∠BOB ′
的度数是( ).
A. 21° B.24° C.45° D.66°
A
O
B
A ′
B ′
C
巩固提高
2.如图,把正△ ABC 绕其中心O旋转一定角度后
与自身重合,则这个旋转角度至少为( ).
A.360° B.240° C.120° D.60°
A
B
C
O
C
①
②
①
②
①
②
①
②
3.下列四组图形中,图①按顺时针方向旋转120°后可以得出图②的那一组是( ).
A B C D
D
4.如图,在 Rt△ACB中,∠C=90°,∠B
=60°,将Rt△ACB绕点 A逆时针旋转70°后得
到△AC′B′,则∠ CAB′=( ).
A. 60° B. 70°
C. 100° D. 120°
A
B
C
C′
B′
C
5.将如图 的“十字星”图形绕其中心点O旋转,
当至少旋转 度后,所得图形与原图形重合.
O
90
今天作业
课本P10页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
24.1图形的旋转(1)
教学目标:
1.通过观察具体实例学习旋转概念,会画一个图形
作旋转后所得的图形;
2.探究旋转的性质,并在观察、猜想、验证、归纳、
概括的探究过程中,发展合情推理能力,进一步
体会图形运动中的变和不变.
教学重点:
旋转的性质.
课件说明
一、引入:
生活中,旋转的现象普遍存在。如:
一、引入:
生活中,旋转的现象普遍存在。如:
1.旋转的概念
在平面内,一个图形绕着一个定点(如点O)按照一定的方向旋转一定的角度θ,得到另一个图形的变换,叫做旋转.
定点O叫做旋转中心,θ叫做旋转角.
原图形上的一点A旋转后成为点A ′ ,
这样的两个点叫做对应点.
θ
学习新知
旋转三要素:
旋转中心
旋转方向
旋转角
θ
如图,△ABC绕着旋转中心O按逆时针旋转θ后,得到△A′B′C′.
2.旋转有什么性质?
(1)连接OA、OB、OC 、OA′、OB′、OC′,那么OA与OA′的长度有何关系?
OB与OB′、OC与OC′也有这样的关系吗
OA=OA ′
OB=OB ′ ,OC=OC ′
每对对应点到旋转中心的距离相等.
学习新知
如图,△ABC绕着旋转中心O按逆时针旋转θ后,得到△A′B′C′.
(2)∠AOA′、∠BOB′、∠COC′有何关系?
2.旋转有什么性质?
∠AOA ′ =∠BOB ′ =∠COC ′
旋转角彼此相等
如图,△ABC绕着旋转中心O按逆时针旋转θ后,得到△A′B′C′.
2.旋转有什么性质?
(3)△ABC和△A′B′C′ 的形状和大小有什么关系?
△ABC≌△A′B′C′
2.旋转的性质:
一个图形和它经过旋转所得到的图形中,
(1)对应点到旋转中心的距离相等;
(2)两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
(3)旋转中心是唯一不动的点.
(4)旋转前后的两个图形是全等形.
在平面内,一个图形绕着一个定点旋转一定角度后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心.
如□ ABCD绕着一个定点O旋转180°能够与原图形重合.
平行四边形是旋转对称图形,
定点O就是旋转中心.
O
A
B
C
D
学习新知
在平面内,一个图形绕着一个定点旋转一定角度后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心.
如图绕着定点O旋转120°或240°能够与原图形重合.
O
旋转180°
1.找出下列旋转对称图形的旋转中心,并指出这个图形至少要旋转多大角度才能与原图形重合.
练习巩固
旋转72°
2.找出下列旋转对称图形的旋转中心,并指出这个图形至少要旋转多大角度才能与原图形重合.
O
72°
3.找出下列旋转对称图形的旋转中心,并指出这个图形至少要旋转多大角度才能与原图形重合.
旋转60°
60°
4.在下列图形中:
(1)指出轴对称图形,并用虚线画出该图形的对称轴(2)指出旋转对称图形,用“ ”号标出该图形的旋转中心, 并指出这个图形至少要旋转多大角度才能与原图形重合.
(1)如何画出旋转后的图形?
(2)如何确定旋转后的对应点的位置?
1.确定旋转中心;
2.确定旋转方向;
3.确定旋转角.
1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连线段的夹角等于旋转角.
课堂小结
(3)对比平移、轴对称,旋转的性质,它们有哪些
相同点和不同点?
1.如图,将△AOB绕点O按逆时针方向旋转45°
得到△A ′ OB ′.若∠AOB=21°,则∠BOB ′
的度数是( ).
A. 21° B.24° C.45° D.66°
A
O
B
A ′
B ′
C
巩固提高
2.如图,把正△ ABC 绕其中心O旋转一定角度后
与自身重合,则这个旋转角度至少为( ).
A.360° B.240° C.120° D.60°
A
B
C
O
C
①
②
①
②
①
②
①
②
3.下列四组图形中,图①按顺时针方向旋转120°后可以得出图②的那一组是( ).
A B C D
D
4.如图,在 Rt△ACB中,∠C=90°,∠B
=60°,将Rt△ACB绕点 A逆时针旋转70°后得
到△AC′B′,则∠ CAB′=( ).
A. 60° B. 70°
C. 100° D. 120°
A
B
C
C′
B′
C
5.将如图 的“十字星”图形绕其中心点O旋转,
当至少旋转 度后,所得图形与原图形重合.
O
90
今天作业
课本P10页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
