24.3圆周角(2) 课件(共25张PPT)
文档属性
| 名称 | 24.3圆周角(2) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
沪科版 九年级下册
24.3圆周角 (2)
教学目标: 1.掌握圆内接四边形的概念和性质; 2.会运用圆内接四边形的性质证明和计算一些问题.
教学重点: 圆内接四边形的概念和性质.
课件说明
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角都相等,等于它所对的圆心角的一半.
同弧或等弧所对的圆周角相等.
相等的圆周角所对的弧也相等.
在同圆或等圆中,
半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
复习旧知
O
A
B
C
D
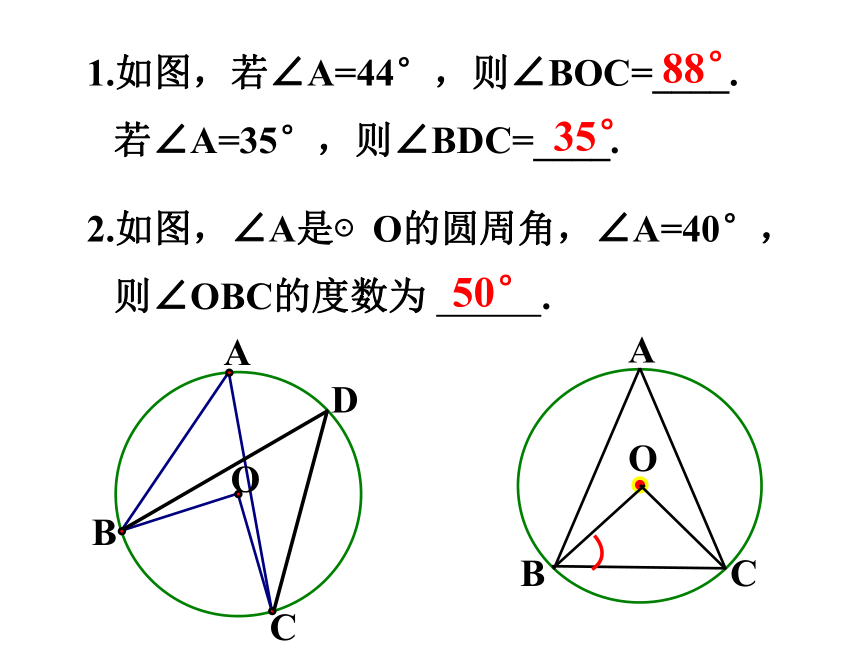
1.如图,若∠A=44°,则∠BOC=____.
若∠A=35°,则∠BDC=____.
88°
35°
2.如图,∠A是⊙O的圆周角,∠A=40°,
则∠OBC的度数为 .
50°
B
O
C
A
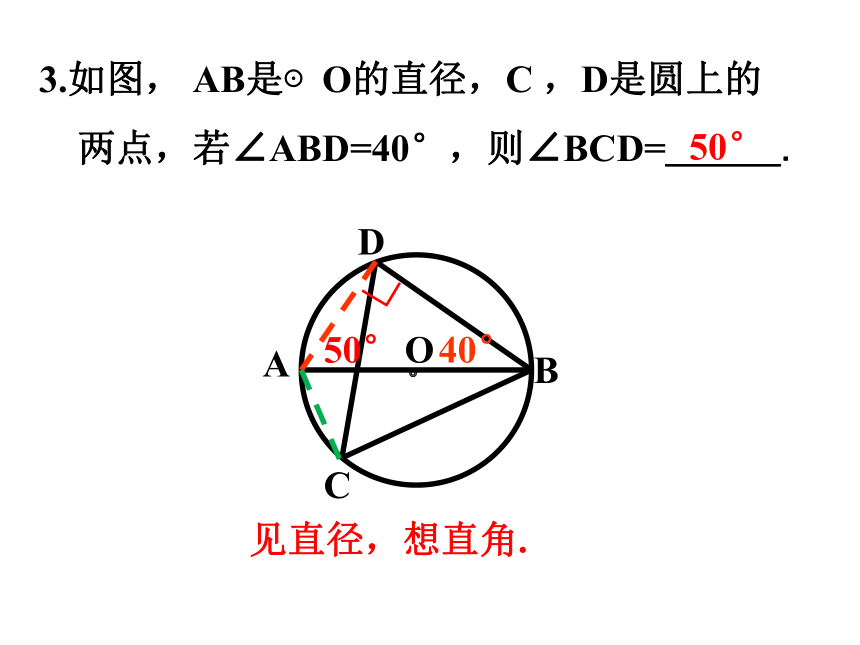
3.如图, AB是⊙O的直径,C ,D是圆上的
两点,若∠ABD=40°,则∠BCD=___.
A
B
O
C
D
40°
50°
50°
见直径,想直角.
*
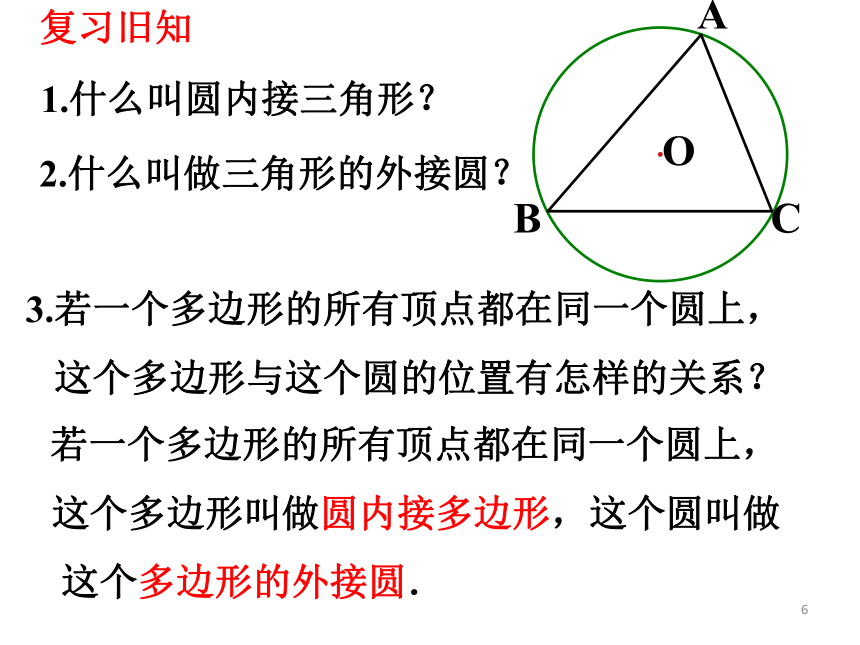
1.什么叫圆内接三角形?
2.什么叫做三角形的外接圆?
A
B
C
O
复习旧知
3.若一个多边形的所有顶点都在同一个圆上,
这个多边形与这个圆的位置有怎样的关系?
若一个多边形的所有顶点都在同一个圆上,
这个多边形叫做圆内接多边形,这个圆叫做
这个多边形的外接圆.
O
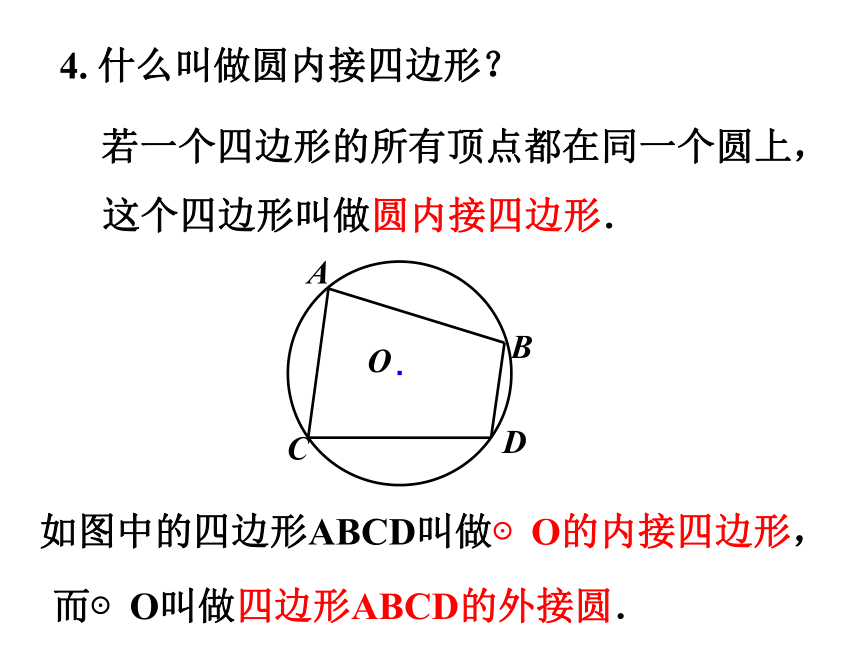
而⊙O叫做四边形ABCD的外接圆.
B
D
A
C
·
4. 什么叫做圆内接四边形?
若一个四边形的所有顶点都在同一个圆上,
这个四边形叫做圆内接四边形.
如图中的四边形ABCD叫做⊙O的内接四边形,
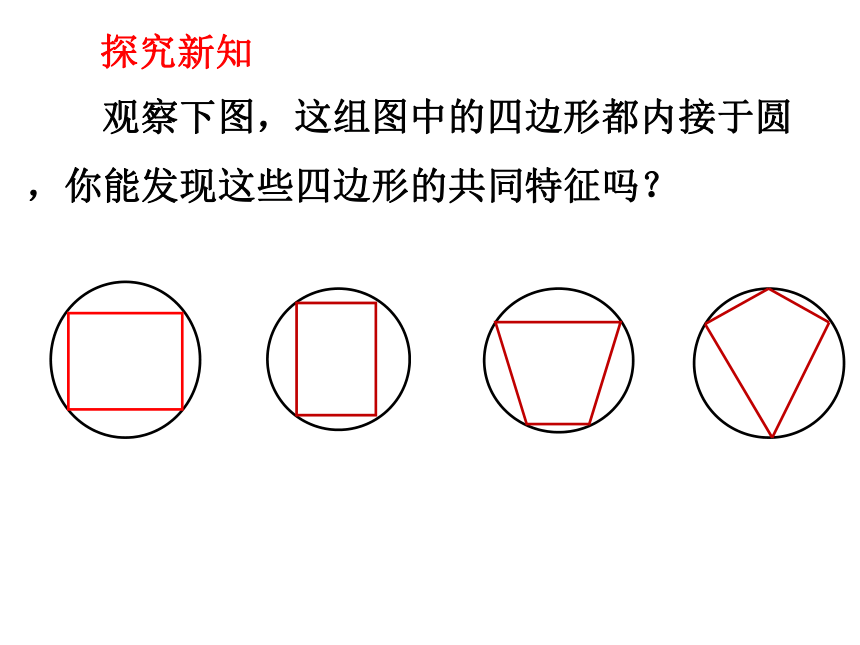
观察下图,这组图中的四边形都内接于圆,你能发现这些四边形的共同特征吗?
探究新知
B
O
C
A
D
A
C
BD
︵
BAD
︵
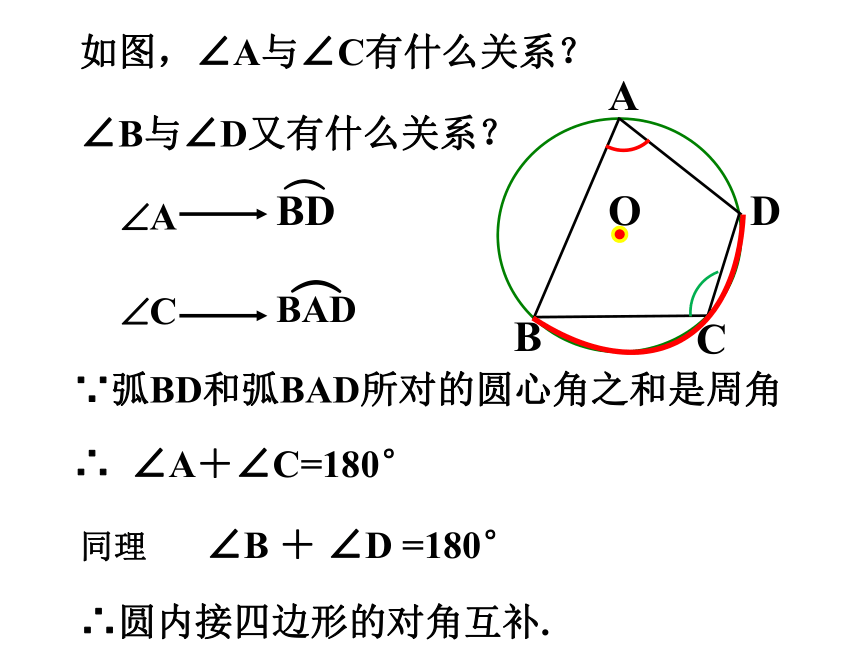
如图,∠A与∠C有什么关系?
∵弧BD和弧BAD所对的圆心角之和是周角
∴圆内接四边形的对角互补.
∴ ∠A+∠C=180°
同理 ∠B + ∠D =180°
∠B与∠D又有什么关系?
A
B
D
C
如图,如果延长BC到E,
E
∴∠A =
∵ ∠A是∠DCE的补角∠BCD的对角,
O
∴圆内接四边形的一个外角等于它的内对角.
DCE
∠DCE
∵∠A+∠BCD=180°
∴ ∠A叫做∠DCE的内对角.
则∠BCD +∠ =180°
E
A
B
D
C
O
定理 圆内接四边形对角互补,且任何一个外角等于它的内对角.
圆内接四边形的性质.
∠A+∠BCD=180°
∠B+∠D=180°
∠A=∠DCE
如图,点A、B、C、D、E都在⊙O上.
①指出图中圆内接四边形的外角有几个?
它们是哪些?
②∠DCH的内对角是哪一个角?
∠DBG呢?
③与∠DEA互补的角是哪个角?
④∠ECB+( )=180°.
B
A
D
C
H
G
F
E
∠EAB
∠ACD
∠ABC
∠DEA
∠DEA
练习巩固
例2 在圆内接四边形 ABCD 中,∠A、∠B、 ∠C 的度数之比是2:3:6,求这个四边形各角的度数.
解:
∵四边形内接于圆,
B+ D=180°,
∴ A=45°,
B=67.5°,
C=135° ,
∴ A+ C=
∴x=22.5°.
=180°-67.5°=112.5 .
∠D=180°-∠B
∴ 2x+6x=180°
设∠A、∠B、 ∠C 的度数分别为2x、3x、6x
1.如图 ,四边形 ABCD是⊙O的内接四边形,∠BOD =100°,求∠BAD和 ∠BCD 的度数.
∵∠BOD =100°,
∴ BAD=50°.
∵ BAD+ BCD=180°.
∴ BCD=130°.
解:
A
B
C
D
O
BAD= ,
BOD
1
2
练习巩固
2.已知 :四边形 ABCD内接于⊙O的四边形, BC是⊙O 的 直径,AD ∥ BC,AC与BD相交于点P,∠APB=20°求四边形ABCD 各个角的度数.
A
B
C
D
O
P
∵ AD ∥ BC ,
解:
∴∠1=∠2,
∵∠1=∠3,
∴∠2=∠3,
1
3
2
∵∠APB=∠2+∠3=20°,
∴∠2=10°.
∵ BC是⊙O的直径,
∴∠BAC=90°.
∴∠ABC=80°.
∴∠BAD=100°.
∴∠ADC=100°,
∴∠DCB=80°.
3.求证 :圆内接平行四边形是矩形.
A
B
C
D
O
∵四边形内接于圆,
∴ A= C,
∴ A+ C=180°.
∴∠A=90°.
已知:如图,□ABCD圆内接于⊙O.
求证:□ABCD是矩形.
∴ □ABCD是矩形.
∵四边形ABCD是平行四边形,
证明:
(1)本节课主要学习了哪些内容?
(2)本节课学到了哪些思想方法?
① 构造圆内接四边形;
② 一题多解,一题多变.
课堂小结
1.如图,四边形ABCD内接于⊙O,连接OB、OD、BD,若∠C=110°,则∠OBD= ( ).
A.10° B. 20° C. 30° D.40°
A
B
C
D
O
B
巩固提高
2.如图,四边形ABCD内接于⊙O,点P为边AD上任一点(点P不与点A,D重合),连接CP,若∠B=110°,则∠APC的度数可能为( ).
A.30° B. 45° C. 50° D.65°
A
B
C
D
O
D
P
3.如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在y轴的正半轴上, ⊙D经过A,B,O,C四点, ∠ACO=120°AB=4,则圆心D坐标是 .
O
x
y
A
B
C
D
(- ,1)
3
4.如图,四边形ABCD是⊙O的内接四边形,连接AC,BD ,延长CD至点E. 若AB=AC,求证: ∠ADB=∠ADE.
A
B
C
D
O
E
证明:
∵四边形ABCD内接于⊙O,
∴ ∠ADE=∠ABC.
∵ AB=AC,
∴ ∠ABC=∠ACB.
∵∠ADB=∠ACB.
∴ ∠ADB=∠ADE.
∴ ∠ADB=∠ABC.
5.如图,AB为⊙O 的直径,直线 a与⊙O 交于点 C、D,BE⊥a于点 E,连接 BD、BC.求证:∠CBE =∠ABD.
A
B
O
D
C
E
a
∵AB是⊙O 的直径,
∴ ADB=90°.
∵BE⊥a于点 E,
∴ BEC=90°.
∴ ADB= BEC.
∴∠CBE =∠ABD.
证明:
连接AD.
∵ A= 1,
∴△ADB∽△CEB,
1
今天作业
课本P31页第3、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
24.3圆周角 (2)
教学目标: 1.掌握圆内接四边形的概念和性质; 2.会运用圆内接四边形的性质证明和计算一些问题.
教学重点: 圆内接四边形的概念和性质.
课件说明
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角都相等,等于它所对的圆心角的一半.
同弧或等弧所对的圆周角相等.
相等的圆周角所对的弧也相等.
在同圆或等圆中,
半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
复习旧知
O
A
B
C
D
1.如图,若∠A=44°,则∠BOC=____.
若∠A=35°,则∠BDC=____.
88°
35°
2.如图,∠A是⊙O的圆周角,∠A=40°,
则∠OBC的度数为 .
50°
B
O
C
A
3.如图, AB是⊙O的直径,C ,D是圆上的
两点,若∠ABD=40°,则∠BCD=___.
A
B
O
C
D
40°
50°
50°
见直径,想直角.
*
1.什么叫圆内接三角形?
2.什么叫做三角形的外接圆?
A
B
C
O
复习旧知
3.若一个多边形的所有顶点都在同一个圆上,
这个多边形与这个圆的位置有怎样的关系?
若一个多边形的所有顶点都在同一个圆上,
这个多边形叫做圆内接多边形,这个圆叫做
这个多边形的外接圆.
O
而⊙O叫做四边形ABCD的外接圆.
B
D
A
C
·
4. 什么叫做圆内接四边形?
若一个四边形的所有顶点都在同一个圆上,
这个四边形叫做圆内接四边形.
如图中的四边形ABCD叫做⊙O的内接四边形,
观察下图,这组图中的四边形都内接于圆,你能发现这些四边形的共同特征吗?
探究新知
B
O
C
A
D
A
C
BD
︵
BAD
︵
如图,∠A与∠C有什么关系?
∵弧BD和弧BAD所对的圆心角之和是周角
∴圆内接四边形的对角互补.
∴ ∠A+∠C=180°
同理 ∠B + ∠D =180°
∠B与∠D又有什么关系?
A
B
D
C
如图,如果延长BC到E,
E
∴∠A =
∵ ∠A是∠DCE的补角∠BCD的对角,
O
∴圆内接四边形的一个外角等于它的内对角.
DCE
∠DCE
∵∠A+∠BCD=180°
∴ ∠A叫做∠DCE的内对角.
则∠BCD +∠ =180°
E
A
B
D
C
O
定理 圆内接四边形对角互补,且任何一个外角等于它的内对角.
圆内接四边形的性质.
∠A+∠BCD=180°
∠B+∠D=180°
∠A=∠DCE
如图,点A、B、C、D、E都在⊙O上.
①指出图中圆内接四边形的外角有几个?
它们是哪些?
②∠DCH的内对角是哪一个角?
∠DBG呢?
③与∠DEA互补的角是哪个角?
④∠ECB+( )=180°.
B
A
D
C
H
G
F
E
∠EAB
∠ACD
∠ABC
∠DEA
∠DEA
练习巩固
例2 在圆内接四边形 ABCD 中,∠A、∠B、 ∠C 的度数之比是2:3:6,求这个四边形各角的度数.
解:
∵四边形内接于圆,
B+ D=180°,
∴ A=45°,
B=67.5°,
C=135° ,
∴ A+ C=
∴x=22.5°.
=180°-67.5°=112.5 .
∠D=180°-∠B
∴ 2x+6x=180°
设∠A、∠B、 ∠C 的度数分别为2x、3x、6x
1.如图 ,四边形 ABCD是⊙O的内接四边形,∠BOD =100°,求∠BAD和 ∠BCD 的度数.
∵∠BOD =100°,
∴ BAD=50°.
∵ BAD+ BCD=180°.
∴ BCD=130°.
解:
A
B
C
D
O
BAD= ,
BOD
1
2
练习巩固
2.已知 :四边形 ABCD内接于⊙O的四边形, BC是⊙O 的 直径,AD ∥ BC,AC与BD相交于点P,∠APB=20°求四边形ABCD 各个角的度数.
A
B
C
D
O
P
∵ AD ∥ BC ,
解:
∴∠1=∠2,
∵∠1=∠3,
∴∠2=∠3,
1
3
2
∵∠APB=∠2+∠3=20°,
∴∠2=10°.
∵ BC是⊙O的直径,
∴∠BAC=90°.
∴∠ABC=80°.
∴∠BAD=100°.
∴∠ADC=100°,
∴∠DCB=80°.
3.求证 :圆内接平行四边形是矩形.
A
B
C
D
O
∵四边形内接于圆,
∴ A= C,
∴ A+ C=180°.
∴∠A=90°.
已知:如图,□ABCD圆内接于⊙O.
求证:□ABCD是矩形.
∴ □ABCD是矩形.
∵四边形ABCD是平行四边形,
证明:
(1)本节课主要学习了哪些内容?
(2)本节课学到了哪些思想方法?
① 构造圆内接四边形;
② 一题多解,一题多变.
课堂小结
1.如图,四边形ABCD内接于⊙O,连接OB、OD、BD,若∠C=110°,则∠OBD= ( ).
A.10° B. 20° C. 30° D.40°
A
B
C
D
O
B
巩固提高
2.如图,四边形ABCD内接于⊙O,点P为边AD上任一点(点P不与点A,D重合),连接CP,若∠B=110°,则∠APC的度数可能为( ).
A.30° B. 45° C. 50° D.65°
A
B
C
D
O
D
P
3.如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在y轴的正半轴上, ⊙D经过A,B,O,C四点, ∠ACO=120°AB=4,则圆心D坐标是 .
O
x
y
A
B
C
D
(- ,1)
3
4.如图,四边形ABCD是⊙O的内接四边形,连接AC,BD ,延长CD至点E. 若AB=AC,求证: ∠ADB=∠ADE.
A
B
C
D
O
E
证明:
∵四边形ABCD内接于⊙O,
∴ ∠ADE=∠ABC.
∵ AB=AC,
∴ ∠ABC=∠ACB.
∵∠ADB=∠ACB.
∴ ∠ADB=∠ADE.
∴ ∠ADB=∠ABC.
5.如图,AB为⊙O 的直径,直线 a与⊙O 交于点 C、D,BE⊥a于点 E,连接 BD、BC.求证:∠CBE =∠ABD.
A
B
O
D
C
E
a
∵AB是⊙O 的直径,
∴ ADB=90°.
∵BE⊥a于点 E,
∴ BEC=90°.
∴ ADB= BEC.
∴∠CBE =∠ABD.
证明:
连接AD.
∵ A= 1,
∴△ADB∽△CEB,
1
今天作业
课本P31页第3、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
