24.2圆的基本性质(3) 课件(共25张PPT)
文档属性
| 名称 | 24.2圆的基本性质(3) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 13:01:03 | ||
图片预览



文档简介
(共25张PPT)
沪科版 九年级下册
24.2圆的基本性质(3)
教学目标: 1.理解圆的轴对称性,会运用垂径定理解决有关的 证明、计算和作图问题; 2.感受类比、转化、数形结合、方程等数学思想和 方法,在实验、观察、猜想、抽象、概括、推理 的过程中发展逻辑思维能力和识图能力.
教学重点: 垂径定理及其推论.
课件说明
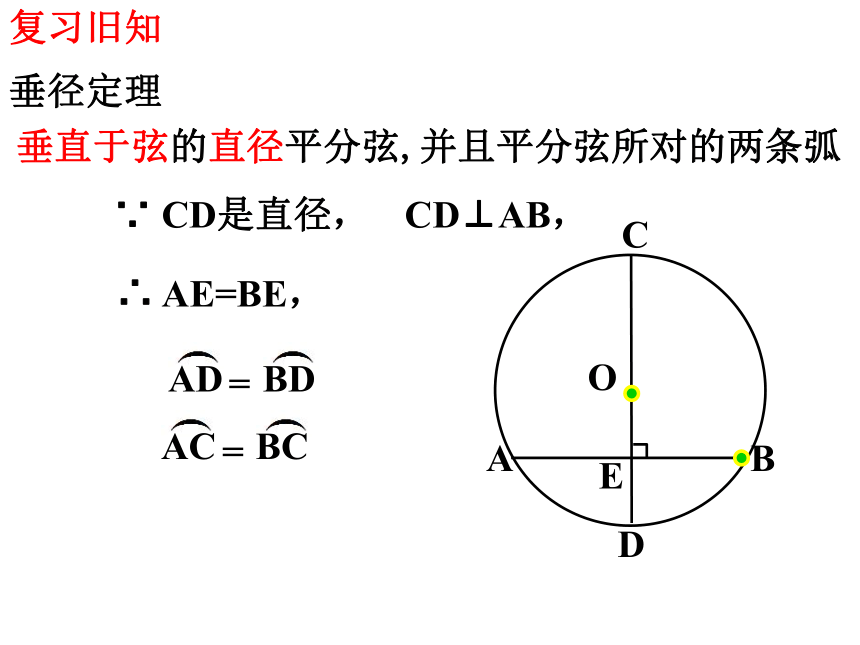
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧
CD⊥AB,
∴ AE=BE,
∵ CD是直径,
AC
BC
=
AD
BD
=
O
D
C
A
B
E
复习旧知
O
O
O
O
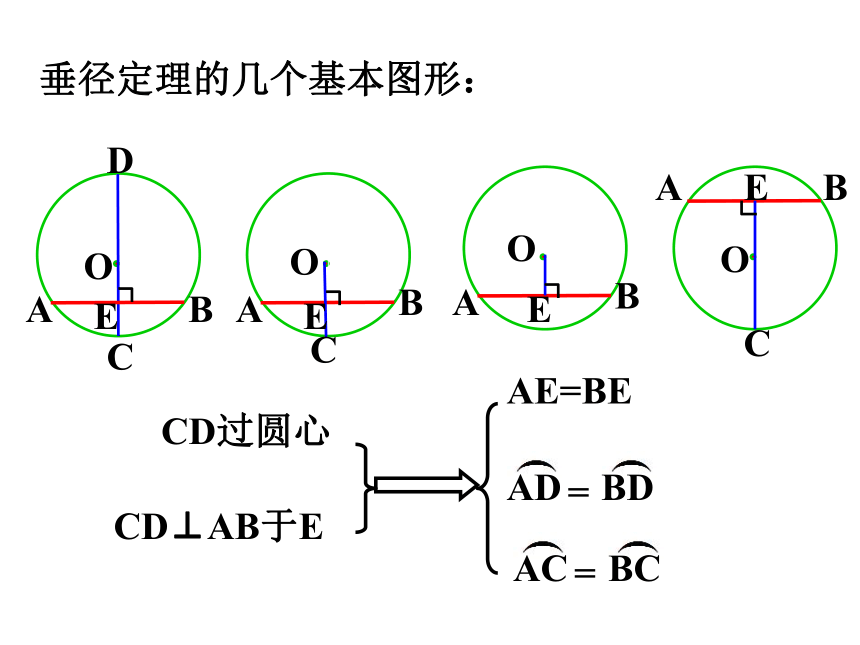
垂径定理的几个基本图形:
CD过圆心
CD⊥AB于E
AE=BE
A
B
A
B
C
D
E
E
C
A
B
E
A
B
C
E
AD
BD
=
AC
BC
=
C
D
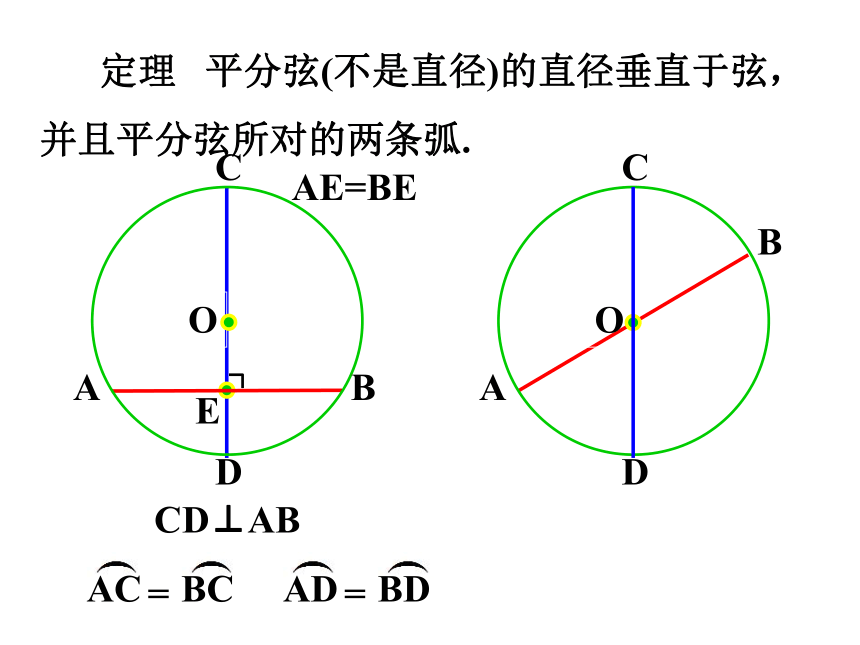
定理 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
O
A
B
O
A
B
C
D
CD⊥AB
AC
BC
=
AD
BD
=
E
AE=BE
·
D
A
C
B
O
E
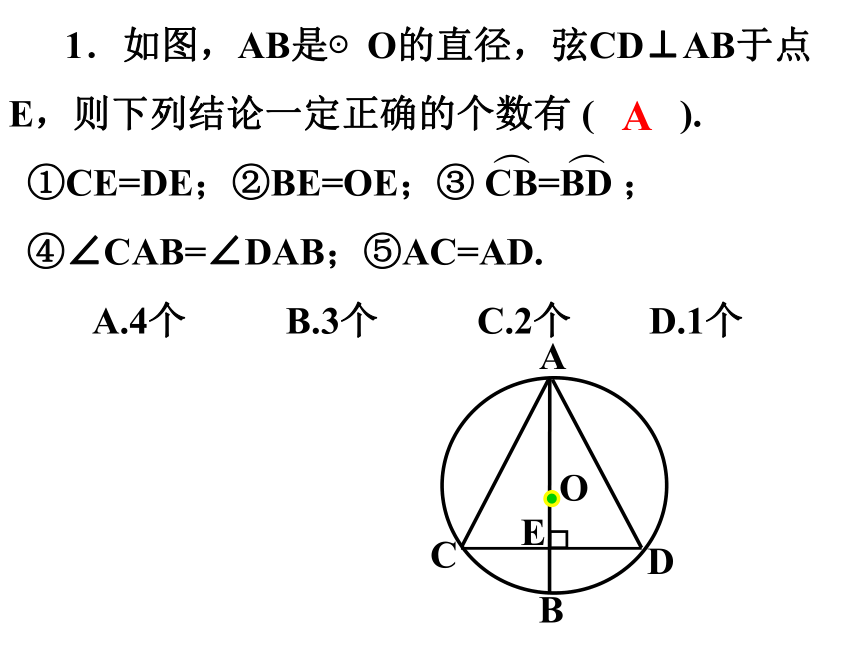
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论一定正确的个数有 ( ).
①CE=DE;②BE=OE;③ CB=BD ;
④∠CAB=∠DAB;⑤AC=AD.
A.4个 B.3个 C.2个 D.1个
︵
︵
A
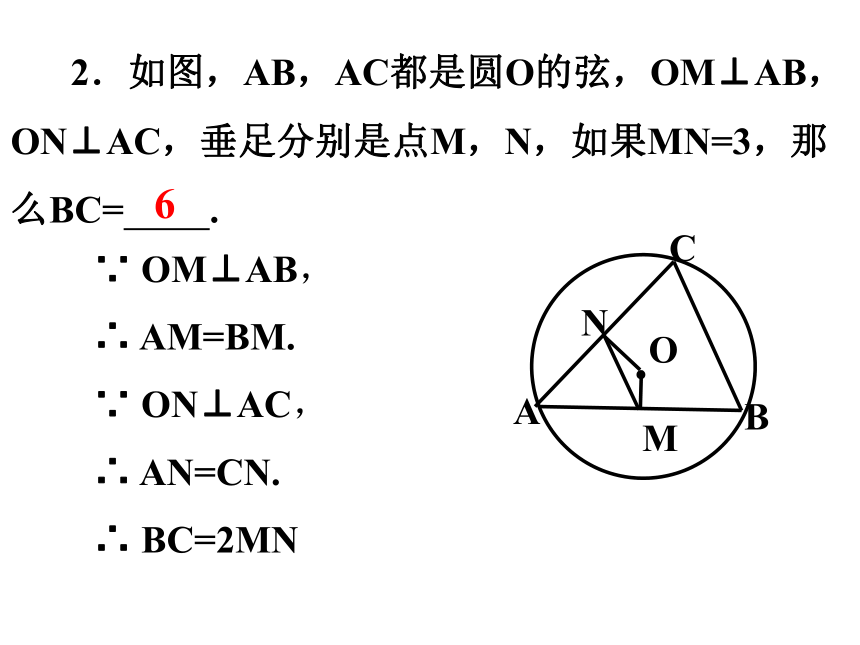
2.如图,AB,AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别是点M,N,如果MN=3,那么BC= .
●
O
M
N
C
B
A
6
∵ ON⊥AC,
∴ AM=BM.
∵ OM⊥AB,
∴ AN=CN.
∴ BC=2MN
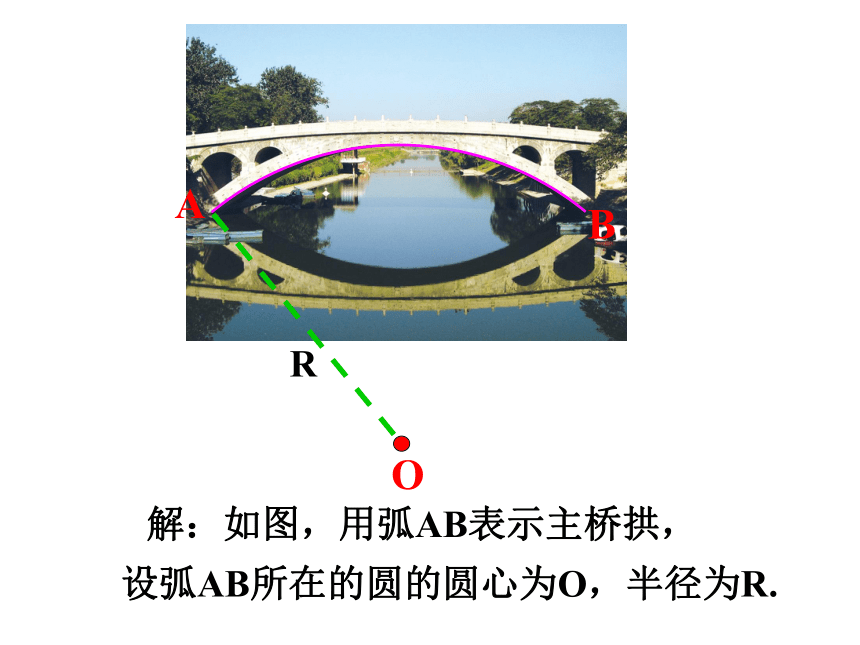
例3 赵州桥建于1 400 年前的隋朝,是我国石拱桥的代表性桥梁,桥的下部呈圆弧形,桥的跨度(弧所对的弦长)是 37 .4m,拱高(弧的中点到弦的距离)为 7.2 m,求赵州桥桥拱所在圆的半径.(精确到 0.1 m).
A
B
O
解:如图,用弧AB表示主桥拱,
设弧AB所在的圆的圆心为O,半径为R.
R
37.4m
7.2m
A
B
O
C
D
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
A
B
O
C
D
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴ AB=37.4m,CD=7.2m.
∴ AD= AB=18.7m,
∵OA2 =AD2+OD2
OD=OC-CD=R-7.2.
∴R2 =18.72+(R-7.2)2
1
2
∵OA2 =AD2+OD2
∴R2 =18.72+(R-7.2)2
∴R2 =349.69+R2-14.4R +51.84.
∴14.4R =401.53
∴ R ≈ 27.9.
(18+0.7)2
18.72=
=182+2×18×0.7 +0.72
=324+25.2 +0.49
=349.69
(7+0.2)2
7.22=
=72+2×7×0.2 +0.22
=49+2.8 +0.04
=51.84
A
B
O
C
D
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴ AB=37.4m,CD=7.2m.
∴ AD= AB=18.7m,
∵OA2 =AD2+OD2
OD=OC-CD=R-7.2.
∴R2 =18.72+(R-7.2)2
1
2
∴ R ≈ 27.9.
答:赵州桥桥拱所在圆的半径约为27.9m.
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线.
弦心距、半径、半弦构成直角三角形,便将问题转化为直角三角形的问题.
A
B
O
C
D
B
A
O
C
1.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD
的高度为 m.
4
练习巩固
2.已知:如图,在以O为圆心的两个同心圆中,大圆弦 AB 交小圆于 C,D两点,求证: AC = BD .
D
O
C
A
B
证明:
过点O作OE⊥AB于E,
E
∴AE=BE ,
CE=DE .
∴AE-CE=BE-DE ,
∴AC=BD .
变式1
如图,连接 OA,OB,设 AO=BO,
求证:AC=BD.
D
O
C
A
B
过点O作OE⊥AB于E,
则有:
∴CE=DE ,
E
∵AO=BO,
OE⊥AB,
∴AE=BE ,
∴AE-CE=BE-DE ,
∴AC=BD .
证明:
变式2
连接 OC,OD,设 OC=OD,求证:AC=BD.
D
O
C
A
B
E
过点O作OE⊥AB于E,
则有:
∴AE=BE ,
∵OC=OD,
OE⊥CD,
∴CE=DE ,
∴AE-CE=BE-DE ,
∴AC=BD .
证明:
3.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证:四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,
AC=AB,
∴ AE=AD,
∴ 四边形ADOE为正方形.
∴ ∠OEA=90°,
∠ODA=90°,
∠DAE=90°,
∵ OE⊥AC,
OD⊥AB,
AB⊥AC,
∵AE= AC,
1
2
AD= AB,
1
2
1.垂径定理的内容是什么?
2.用垂径定理解决有关证明、计算问题的思路是什么?
①构造直角三角形,垂径定理和勾股定理有机结合是计算弦长、半径和弦心距等问题的方法.
②技巧:重要辅助线是过圆心作弦的垂线.
(由)垂径定理—构造直角三角形—
(结合)勾股定理—建立方程.
课堂小结
1.如图,AB是⊙O的直径,且经过弦CD的中点H. 已知sin∠CDB = ,BD= 5 ,则AH的长是( ).
A. B. C. D.
巩固提高
3
5
O
H
B
C
D
A
3
25
3
16
6
25
6
16
B
2.如图,AB是⊙O的弦,OC ⊥ AB,垂足为点C. 将AB沿弦AB折叠交于OC的中点D,若AB ,则的半径为 .
100
=2
10
3.某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道.如图,污水水面宽度AB为60 cm,水面到管道顶部距离为10 cm.求修理人员应准备内径为 厘米的管道(内径指内部直径).
O
B
C
D
A
O
B
A
3
2
C
︵
今天作业
课本P26页第8题
课本P25页第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
24.2圆的基本性质(3)
教学目标: 1.理解圆的轴对称性,会运用垂径定理解决有关的 证明、计算和作图问题; 2.感受类比、转化、数形结合、方程等数学思想和 方法,在实验、观察、猜想、抽象、概括、推理 的过程中发展逻辑思维能力和识图能力.
教学重点: 垂径定理及其推论.
课件说明
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧
CD⊥AB,
∴ AE=BE,
∵ CD是直径,
AC
BC
=
AD
BD
=
O
D
C
A
B
E
复习旧知
O
O
O
O
垂径定理的几个基本图形:
CD过圆心
CD⊥AB于E
AE=BE
A
B
A
B
C
D
E
E
C
A
B
E
A
B
C
E
AD
BD
=
AC
BC
=
C
D
定理 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
O
A
B
O
A
B
C
D
CD⊥AB
AC
BC
=
AD
BD
=
E
AE=BE
·
D
A
C
B
O
E
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论一定正确的个数有 ( ).
①CE=DE;②BE=OE;③ CB=BD ;
④∠CAB=∠DAB;⑤AC=AD.
A.4个 B.3个 C.2个 D.1个
︵
︵
A
2.如图,AB,AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别是点M,N,如果MN=3,那么BC= .
●
O
M
N
C
B
A
6
∵ ON⊥AC,
∴ AM=BM.
∵ OM⊥AB,
∴ AN=CN.
∴ BC=2MN
例3 赵州桥建于1 400 年前的隋朝,是我国石拱桥的代表性桥梁,桥的下部呈圆弧形,桥的跨度(弧所对的弦长)是 37 .4m,拱高(弧的中点到弦的距离)为 7.2 m,求赵州桥桥拱所在圆的半径.(精确到 0.1 m).
A
B
O
解:如图,用弧AB表示主桥拱,
设弧AB所在的圆的圆心为O,半径为R.
R
37.4m
7.2m
A
B
O
C
D
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
A
B
O
C
D
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴ AB=37.4m,CD=7.2m.
∴ AD= AB=18.7m,
∵OA2 =AD2+OD2
OD=OC-CD=R-7.2.
∴R2 =18.72+(R-7.2)2
1
2
∵OA2 =AD2+OD2
∴R2 =18.72+(R-7.2)2
∴R2 =349.69+R2-14.4R +51.84.
∴14.4R =401.53
∴ R ≈ 27.9.
(18+0.7)2
18.72=
=182+2×18×0.7 +0.72
=324+25.2 +0.49
=349.69
(7+0.2)2
7.22=
=72+2×7×0.2 +0.22
=49+2.8 +0.04
=51.84
A
B
O
C
D
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴ AB=37.4m,CD=7.2m.
∴ AD= AB=18.7m,
∵OA2 =AD2+OD2
OD=OC-CD=R-7.2.
∴R2 =18.72+(R-7.2)2
1
2
∴ R ≈ 27.9.
答:赵州桥桥拱所在圆的半径约为27.9m.
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线.
弦心距、半径、半弦构成直角三角形,便将问题转化为直角三角形的问题.
A
B
O
C
D
B
A
O
C
1.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD
的高度为 m.
4
练习巩固
2.已知:如图,在以O为圆心的两个同心圆中,大圆弦 AB 交小圆于 C,D两点,求证: AC = BD .
D
O
C
A
B
证明:
过点O作OE⊥AB于E,
E
∴AE=BE ,
CE=DE .
∴AE-CE=BE-DE ,
∴AC=BD .
变式1
如图,连接 OA,OB,设 AO=BO,
求证:AC=BD.
D
O
C
A
B
过点O作OE⊥AB于E,
则有:
∴CE=DE ,
E
∵AO=BO,
OE⊥AB,
∴AE=BE ,
∴AE-CE=BE-DE ,
∴AC=BD .
证明:
变式2
连接 OC,OD,设 OC=OD,求证:AC=BD.
D
O
C
A
B
E
过点O作OE⊥AB于E,
则有:
∴AE=BE ,
∵OC=OD,
OE⊥CD,
∴CE=DE ,
∴AE-CE=BE-DE ,
∴AC=BD .
证明:
3.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证:四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,
AC=AB,
∴ AE=AD,
∴ 四边形ADOE为正方形.
∴ ∠OEA=90°,
∠ODA=90°,
∠DAE=90°,
∵ OE⊥AC,
OD⊥AB,
AB⊥AC,
∵AE= AC,
1
2
AD= AB,
1
2
1.垂径定理的内容是什么?
2.用垂径定理解决有关证明、计算问题的思路是什么?
①构造直角三角形,垂径定理和勾股定理有机结合是计算弦长、半径和弦心距等问题的方法.
②技巧:重要辅助线是过圆心作弦的垂线.
(由)垂径定理—构造直角三角形—
(结合)勾股定理—建立方程.
课堂小结
1.如图,AB是⊙O的直径,且经过弦CD的中点H. 已知sin∠CDB = ,BD= 5 ,则AH的长是( ).
A. B. C. D.
巩固提高
3
5
O
H
B
C
D
A
3
25
3
16
6
25
6
16
B
2.如图,AB是⊙O的弦,OC ⊥ AB,垂足为点C. 将AB沿弦AB折叠交于OC的中点D,若AB ,则的半径为 .
100
=2
10
3.某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道.如图,污水水面宽度AB为60 cm,水面到管道顶部距离为10 cm.求修理人员应准备内径为 厘米的管道(内径指内部直径).
O
B
C
D
A
O
B
A
3
2
C
︵
今天作业
课本P26页第8题
课本P25页第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
