2023年江苏省普通高中学业水平合格性考试数学模拟试卷(五)(含答案)
文档属性
| 名称 | 2023年江苏省普通高中学业水平合格性考试数学模拟试卷(五)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 67.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 12:51:58 | ||
图片预览



文档简介
2023江苏省普通高中学业水平合格性考试
数学模拟试卷(五)
(考试时间:90分钟 满分:150分)
一、 单选题(共28题,每题3分,共84分)
1. 命题“ x>0,2x<1”的否定是 ( )
A. x>0,2x≥1 B. x<0,2x≥1
C. x>0,2x≥1 D. x<0,2x<1
2. 若集合A={1,2,3,4,5},B={x|y=ln(3-x)},则集合A∩B的子集个数为 ( )
A. 2 B. 3 C. 4 D. 5
3. 若复数z满足(z-1)i=1+i,则z在复平面内对应的点在 ( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
4. 若cos=,sin 2α= ( )
A. B. - C. - D.
5. 已知幂函数y=(m2-3m+3)的图象不过原点,则实数m的值为 ( )
A. 1 B. 2 C. -2 D. 1或2
6. 已知集合A={x|x2-6x+8<0},B={x|a≤x≤a+1},若A∪B=A,则实数a的取值范围为 ( )
A. (1,3) B. [1,3] C. (2,3) D. [2,3]
7. 已知向量a=(k,1),b=(4,k),c=(k+1,-2),若a∥b且a⊥c,则k= ( )
A. 0 B. -2 C. 2 D. ±2
8. 函数f(x)=-log5x-x+3的零点所在区间为 ( )
A. (1,2) B. (2,3) C. (3,4) D. (4,5)
9. 某单位有200名职工,其中女职工有60人,男职工有140人,现要从中抽取30人进行调研座谈,如果用比例分配的分层随机抽样的方法进行抽样,则应抽女职工 ( )
A. 6人 B. 9人 C. 10人 D. 30人
10. 在△ABC中,a,b,c分别是内角A,B,C的对边,且2acos C=2b+c,则角A等于 ( )
A. B. C. D.
11. 一袋中装有除颜色外完全相同的4个白球和5个黑球,从中有放回地摸球3次,每次摸一个球.用模拟实验的方法,让计算机产生19的随机数,若14代表白球,59代表黑球,每三个为1组,产生如下20组随机数:
917 966 191 925 271 932 735 458 569 683
431 257 393 627 556 488 812 184 537 989
则三次摸出的球中恰好有两次是白球的概率近似为 ( )
A. B. C. D.
12. 已知“ x∈R,使得不等式x2-4x-a-1<0”是假命题,则a的取值范围为 ( )
A. (-∞,-5] B. (-∞,-2]
C. (-5,+∞) D. [-5,+∞)
13. 若tan α=2,则4sin2 α-3sin αcos α-5cos2 α的值为 ( )
A. 0 B. 1 C. D. 2
14. 已知b,c∈R,关于x的不等式x2+bx+c<0的解集为(-2,1),则关于x的不等式cx2+bx+1>0的解集为( )
A. B.
C. ∪(1,+∞) D. (-∞,-1)∪
15. 若某群体中的成员只用现金支付的概率为0.2,不用现金支付的概率为0.45,则既用现金支付也用非现金支付的概率为 ( )
A. 0.35 B. 0.65 C. 0.25 D. 0
16. 函数f(x)=2cos+1的单调减区间是 ( )
A. (k∈Z)
B. (k∈Z)
C. (k∈Z)
D. (k∈Z)
17. 已知复数z=(m2-2m)+(m2-4)i(m∈R),则下列结论中错误的是 ( )
A. 当m=2时,z是实数
B. 当m=0时,z是纯虚数
C. 当m=-2时,z+=0
D. 当m=1时,z是方程x2+2x+10=0的一个根
18. 已知空间两条不同的直线a,b和两个不重合的平面α,β,下列命题中正确的是 ( )
A. 若a∥b,b α,则a∥α
B. 若a⊥β,a⊥b,b α,则α∥β
C. 若a∥α,α⊥β,则a⊥β
D. 若a⊥α,b⊥β,α⊥β,则a⊥b
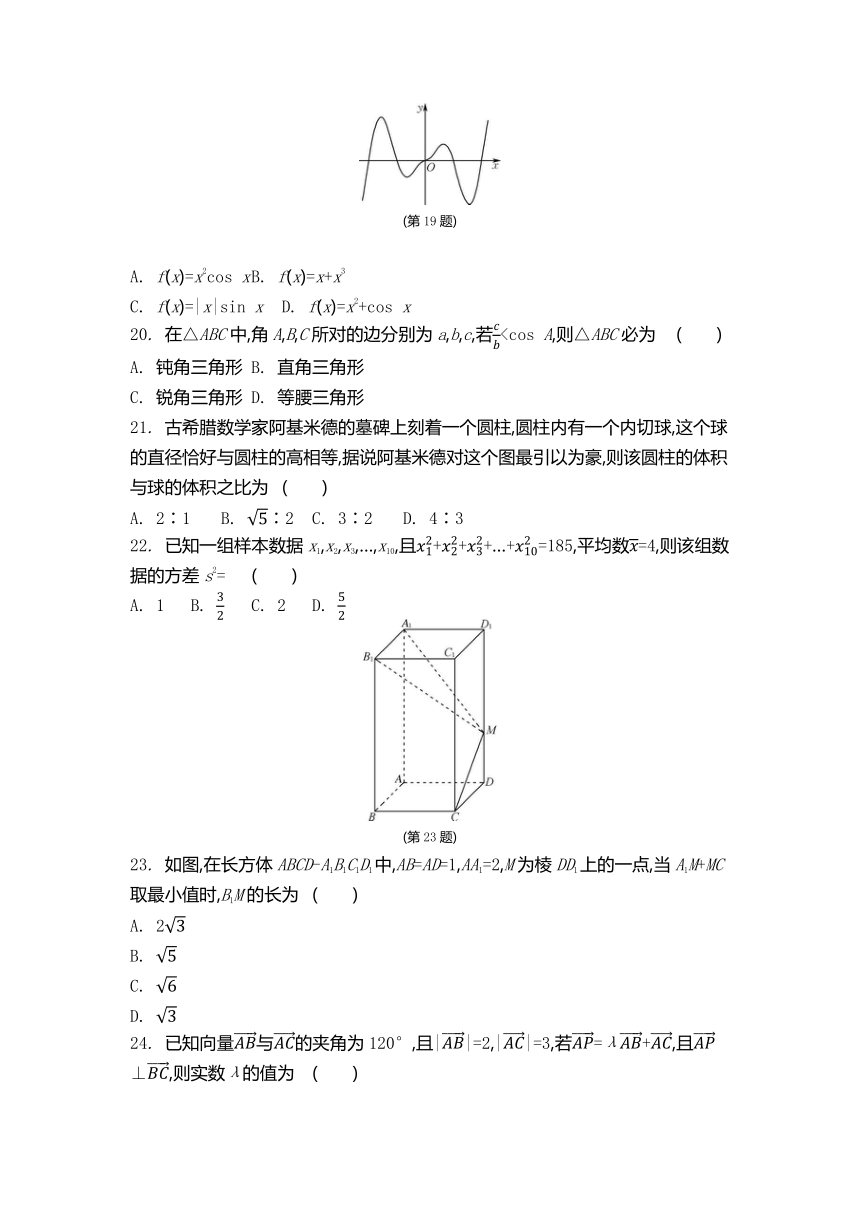
19. 已知函数f(x)的部分图象如图所示,则f(x)的解析式可能为 ( )
(第19题)
A. f(x)=x2cos x B. f(x)=x+x3
C. f(x)=|x|sin x D. f(x)=x2+cos x
20. 在△ABC中,角A,B,C所对的边分别为a,b,c,若A. 钝角三角形 B. 直角三角形
C. 锐角三角形 D. 等腰三角形
21. 古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,据说阿基米德对这个图最引以为豪,则该圆柱的体积与球的体积之比为 ( )
A. 2∶1 B. ∶2 C. 3∶2 D. 4∶3
22. 已知一组样本数据x1,x2,x3,…,x10,且+++…+=185,平均数=4,则该组数据的方差s2= ( )
A. 1 B. C. 2 D.
(第23题)
23. 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点,当A1M+MC取最小值时,B1M的长为 ( )
A. 2
B.
C.
D.
24. 已知向量与的夹角为120°,且||=2,||=3,若=λ+,且⊥,则实数λ的值为 ( )
A. B. 13 C. 6 D.
25. 已知cos(α-β)=,cos 2α=,α∈,β∈(0,π),且α<β,则α+β= ( )
A. B. C. D.
26. 已知函数f(x)=3x5+x3+5x+2,若f(a)+f(2a-1)>4,则实数a的取值范围是 ( )
A. B.
C. (-∞,3) D. (3,+∞)
27. 已知函数y=ax-1+3(a>0,且a≠1)的图象恒过点P(m,n),正实数p,q满足mp+nq=1,则+的最小值是( )
A. 9 B. 12 C. 3 D. 6
28. 神舟十二号载人飞船搭载3名宇航员进入太空,在中国空间站完成了为期三个月的太空驻留任务,期间进行了很多空间实验,目前已经顺利返回地球.在太空中水资源有限,要通过回收水的方法制造可用水.回收水是将宇航员的尿液、汗液和太空中的水收集起来经过特殊的净水器处理成饮用水,循环使用.净化水的过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少需要过滤的次数为(参考数据lg 2=0.301 0) ( )
A. 10 B. 12 C. 14 D. 16
二、 解答题(共2题,每题8分,共16分)
29. 某水果店的店长为了解本店苹果的日销售情况,记录了过去20天苹果的日销售量(单位:kg),结果如下:83,96,75,91,70,107,100,80,97,94,76,89,117,98,74,95,84,85,87,102.
(1) 计算该水果店过去20天苹果日销售量的中位数、平均数和极差;
(2) 一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求,店长希望每天的苹果尽量新鲜,又能80%地满足顾客的需求(在100天中,大约有80天可以满足顾客的需求),试问每天应进多少千克苹果
30. 已知函数f(x)=-是奇函数.
(1) 求a的值,并根据定义证明函数f(x)在R上单调递增;
(2) 求f(x)的值域.
2023江苏省普通高中学业水平合格性考试数学模拟试卷(五)
数学参考答案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
C C D B A C B B B D B A B A A
16 17 18 19 20 21 22 23 24 25 26 27 28
A C D C A C D D D B A D C
1. C
2. C 解析:集合B={x|y=ln(3-x)}={x|x<3},而集合A={1,2,3,4,5},故A∩B={1,2},因此集合A∩B的子集个数为22=4.
3. D 解析:因为(z-1)i=1+i,所以z=+1=+1=2-i,所以复数z在复平面内对应的点(2,-1)在第四象限.
4. B 解析:由题意可知,sin 2α=cos=cos=2×-1=-.
5. A 解析:由题意可知解得m=1,经经验,符合题意.
6. C 解析:由题意知A={x|x2-6x+8<0}={x|27. B 解析:因为a∥b,a⊥c,所以解得k=-2.
8. B 解析:因为f(x)在(0,+∞)上单调递减,且f(2)=-log52+1>0,f(3)=-log53<0,所以f(x)=-log5x-x+3的零点所在区间为(2,3).
9. B 解析:设应抽女职工x名,则=,解得x=9.
10. D 解析:由2b+c=2acos C=2a×,则b2+c2-a2=-bc,所以cos A==-.又A∈(0,π),所以A=.
11. B 解析:20组随机数恰好有两个是1,2,3,4的有191,271,932,393,812,184,共6个,因此所求概率为=.
12. A 解析:由题知,不等式x2-4x-a-1≥0对 x∈R恒成立,等价于x∈R时a≤(x2-4x-1)min.因为(x2-4x-1)min=-5,所以a≤-5.
13. B 解析:4sin2α-3sin αcos α-5cos2α=====1.
14. A 解析:因为不等式x2+bx+c<0的解集为(-2,1),所以即不等式cx2+bx+1>0等价于-2x2+x+1>0,解得-15. A 解析:支付方式包含3种方法:只用现金支付,不用现金支付,既用现金也用非现金支付,且这三种支付方法是互斥事件,所以既用现金也用非现金支付的概率p=1-0.2-0.45=0.35.
16. A 解析:f(x)=2cos+1=2cos+1,令2x-∈[2kπ,2kπ+π],k∈Z,则x∈,k∈Z,所以函数f(x)的单调减区间为,k∈Z.
17. C 解析:对A,当m=2时,z=0,此时z是实数,故A正确;对B,当m=0时,z=-4i,此时z是纯虚数,故B正确;对C,当m=-2时,z=8,则z+=16,故C错误;对D,当m=1时,z=-1-3i,(-1-3i)2+2(-1-3i)+10=1-9+6i-2-6i+10=0,故D正确.
18. D 解析:若a∥b,b α,则a∥α或a α,故A错误;若a⊥β,a⊥b,b α,则α∥β或α与β相交,故B错误;若a∥α,α⊥β,则a∥β或a β或a与β相交,故C错误;若a⊥α,α⊥β,则a∥β或a β,又由b⊥β,所以a⊥b,故D正确.
19. C 解析:由图可知,f(x)的图象关于原点对称,是奇函数.对于A,D,f(-x)=x2cos x=f(x),f(-x)=x2+cos x=f(x),则函数f(x)=x2cos x,f(x)=x2+cos x是偶函数,排除A和D.当x>0时,f(x)=x+x3>0恒成立,排除B,故选C.
20. A 解析:因为0,cos B<0,所以B∈,所以△ABC为钝角三角形.
21. C 解析:由题意,圆柱底面半径r等于球的半径R,圆柱的高h=2R,则V球=πR3,V柱=πr2h=π·R2·2R=2πR3,所以==.
22. D 解析:由题意可知,x1+x2+x3+…+x10=4×10=40,因为s2==
==.
23. D 解析:如图所示,将侧面AA1D1D、侧面CDD1C1延展至同一平面,当A1,M,C三点共线时,A1M+MC取最小值,易知四边形AA1C1C为正方形,则∠CA1C1=45°,且△A1D1M为等腰直角三角形,所以D1M=A1D1=1.在长方体ABCD-A1B1C1D1中,A1M=,因为A1B1⊥平面AA1D1D,A1M 平面AA1D1D,所以A1B1⊥A1M,因此B1M==.
(第23题)
24. D 解析:由向量与的夹角为120°,且||=2,||=3,可得·=6cos 120°=-3.又⊥,所以·=(λ+)·(-)=(λ-1)·+-λ=12-7λ=0,所以λ=.
25. B 解析:因为α∈,β∈(0,π)且α<β,所以α-β∈(-π,0),2α∈(0,π),所以sin(α-β)=-,sin 2α=,所以cos(α+β)=cos[2α-(α-β)]=cos 2αcos(α-β)+sin 2αsin(α-β)=×+×=-.又sin(α+β)=sin[2α-(α-β)]=sin 2αcos(α-β)-cos 2αsin(α-β)=×-×=.因为α+β∈,所以α+β=.
26. A 解析:设g(x)=f(x)-2,x∈R,则g(-x)=3(-x)5+(-x)3+5(-x)=-(3x5+x3+5x)=-g(x),则g(x)为奇函数,且易知g(x)在R上单调递增.又f(a)+f(2a-1)>4可化为f(a)-2>-[f(2a-1)-2] g(a)>-g(2a-1)=g(1-2a),所以a>1-2a,所以a>.
27. D 解析:函数y=ax-1+3(a>0,且a≠1)的图象恒过点P(1,4),则m=1,n=4,则p+4q=1,则+=+=+4≥2+4=6.
28. C 解析:设过滤的次数为n,原来水中杂质为1,则(1-20%)n<5%,即0.8n<,所以lg0.8n==≈13.4.因为n∈N*,所以n的最小值为14,则至少要过滤14次.
29. 解析:(1) 将数据从小到大排列为:70,74,75,76,80,83,84,85,87,89,91,94,95,96,97,98,100,102,107,117,所以中位数为×(89+91)=90,平均数为×(70+74+75+76+80+83+84+85+87+89+91+94+95+96+97+98+100+102+107+117)=90,极差为117-70=47.
(2) 因为20×80%=16,所以样本数据的第80百分位数是第16、17项数据的平均值,即×(98+100)=99,据此估计每天应进99 kg苹果.
30. 解析:(1)由题知f(-x)=-f(x),则-=-,所以a=1,即f(x)=-.
令x1>x2,则f(x1)-f(x2)=--=-=,又y=2x单调递增,
所以->0,+1>0,+1>0,即f(x1)>f(x2),所以f(x)在R上单调递增.
(2) 由y=2x+1∈(1,+∞),则-∈(-1,0),所以f(x)=-∈.
数学模拟试卷(五)
(考试时间:90分钟 满分:150分)
一、 单选题(共28题,每题3分,共84分)
1. 命题“ x>0,2x<1”的否定是 ( )
A. x>0,2x≥1 B. x<0,2x≥1
C. x>0,2x≥1 D. x<0,2x<1
2. 若集合A={1,2,3,4,5},B={x|y=ln(3-x)},则集合A∩B的子集个数为 ( )
A. 2 B. 3 C. 4 D. 5
3. 若复数z满足(z-1)i=1+i,则z在复平面内对应的点在 ( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
4. 若cos=,sin 2α= ( )
A. B. - C. - D.
5. 已知幂函数y=(m2-3m+3)的图象不过原点,则实数m的值为 ( )
A. 1 B. 2 C. -2 D. 1或2
6. 已知集合A={x|x2-6x+8<0},B={x|a≤x≤a+1},若A∪B=A,则实数a的取值范围为 ( )
A. (1,3) B. [1,3] C. (2,3) D. [2,3]
7. 已知向量a=(k,1),b=(4,k),c=(k+1,-2),若a∥b且a⊥c,则k= ( )
A. 0 B. -2 C. 2 D. ±2
8. 函数f(x)=-log5x-x+3的零点所在区间为 ( )
A. (1,2) B. (2,3) C. (3,4) D. (4,5)
9. 某单位有200名职工,其中女职工有60人,男职工有140人,现要从中抽取30人进行调研座谈,如果用比例分配的分层随机抽样的方法进行抽样,则应抽女职工 ( )
A. 6人 B. 9人 C. 10人 D. 30人
10. 在△ABC中,a,b,c分别是内角A,B,C的对边,且2acos C=2b+c,则角A等于 ( )
A. B. C. D.
11. 一袋中装有除颜色外完全相同的4个白球和5个黑球,从中有放回地摸球3次,每次摸一个球.用模拟实验的方法,让计算机产生19的随机数,若14代表白球,59代表黑球,每三个为1组,产生如下20组随机数:
917 966 191 925 271 932 735 458 569 683
431 257 393 627 556 488 812 184 537 989
则三次摸出的球中恰好有两次是白球的概率近似为 ( )
A. B. C. D.
12. 已知“ x∈R,使得不等式x2-4x-a-1<0”是假命题,则a的取值范围为 ( )
A. (-∞,-5] B. (-∞,-2]
C. (-5,+∞) D. [-5,+∞)
13. 若tan α=2,则4sin2 α-3sin αcos α-5cos2 α的值为 ( )
A. 0 B. 1 C. D. 2
14. 已知b,c∈R,关于x的不等式x2+bx+c<0的解集为(-2,1),则关于x的不等式cx2+bx+1>0的解集为( )
A. B.
C. ∪(1,+∞) D. (-∞,-1)∪
15. 若某群体中的成员只用现金支付的概率为0.2,不用现金支付的概率为0.45,则既用现金支付也用非现金支付的概率为 ( )
A. 0.35 B. 0.65 C. 0.25 D. 0
16. 函数f(x)=2cos+1的单调减区间是 ( )
A. (k∈Z)
B. (k∈Z)
C. (k∈Z)
D. (k∈Z)
17. 已知复数z=(m2-2m)+(m2-4)i(m∈R),则下列结论中错误的是 ( )
A. 当m=2时,z是实数
B. 当m=0时,z是纯虚数
C. 当m=-2时,z+=0
D. 当m=1时,z是方程x2+2x+10=0的一个根
18. 已知空间两条不同的直线a,b和两个不重合的平面α,β,下列命题中正确的是 ( )
A. 若a∥b,b α,则a∥α
B. 若a⊥β,a⊥b,b α,则α∥β
C. 若a∥α,α⊥β,则a⊥β
D. 若a⊥α,b⊥β,α⊥β,则a⊥b
19. 已知函数f(x)的部分图象如图所示,则f(x)的解析式可能为 ( )
(第19题)
A. f(x)=x2cos x B. f(x)=x+x3
C. f(x)=|x|sin x D. f(x)=x2+cos x
20. 在△ABC中,角A,B,C所对的边分别为a,b,c,若
C. 锐角三角形 D. 等腰三角形
21. 古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,据说阿基米德对这个图最引以为豪,则该圆柱的体积与球的体积之比为 ( )
A. 2∶1 B. ∶2 C. 3∶2 D. 4∶3
22. 已知一组样本数据x1,x2,x3,…,x10,且+++…+=185,平均数=4,则该组数据的方差s2= ( )
A. 1 B. C. 2 D.
(第23题)
23. 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点,当A1M+MC取最小值时,B1M的长为 ( )
A. 2
B.
C.
D.
24. 已知向量与的夹角为120°,且||=2,||=3,若=λ+,且⊥,则实数λ的值为 ( )
A. B. 13 C. 6 D.
25. 已知cos(α-β)=,cos 2α=,α∈,β∈(0,π),且α<β,则α+β= ( )
A. B. C. D.
26. 已知函数f(x)=3x5+x3+5x+2,若f(a)+f(2a-1)>4,则实数a的取值范围是 ( )
A. B.
C. (-∞,3) D. (3,+∞)
27. 已知函数y=ax-1+3(a>0,且a≠1)的图象恒过点P(m,n),正实数p,q满足mp+nq=1,则+的最小值是( )
A. 9 B. 12 C. 3 D. 6
28. 神舟十二号载人飞船搭载3名宇航员进入太空,在中国空间站完成了为期三个月的太空驻留任务,期间进行了很多空间实验,目前已经顺利返回地球.在太空中水资源有限,要通过回收水的方法制造可用水.回收水是将宇航员的尿液、汗液和太空中的水收集起来经过特殊的净水器处理成饮用水,循环使用.净化水的过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少需要过滤的次数为(参考数据lg 2=0.301 0) ( )
A. 10 B. 12 C. 14 D. 16
二、 解答题(共2题,每题8分,共16分)
29. 某水果店的店长为了解本店苹果的日销售情况,记录了过去20天苹果的日销售量(单位:kg),结果如下:83,96,75,91,70,107,100,80,97,94,76,89,117,98,74,95,84,85,87,102.
(1) 计算该水果店过去20天苹果日销售量的中位数、平均数和极差;
(2) 一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求,店长希望每天的苹果尽量新鲜,又能80%地满足顾客的需求(在100天中,大约有80天可以满足顾客的需求),试问每天应进多少千克苹果
30. 已知函数f(x)=-是奇函数.
(1) 求a的值,并根据定义证明函数f(x)在R上单调递增;
(2) 求f(x)的值域.
2023江苏省普通高中学业水平合格性考试数学模拟试卷(五)
数学参考答案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
C C D B A C B B B D B A B A A
16 17 18 19 20 21 22 23 24 25 26 27 28
A C D C A C D D D B A D C
1. C
2. C 解析:集合B={x|y=ln(3-x)}={x|x<3},而集合A={1,2,3,4,5},故A∩B={1,2},因此集合A∩B的子集个数为22=4.
3. D 解析:因为(z-1)i=1+i,所以z=+1=+1=2-i,所以复数z在复平面内对应的点(2,-1)在第四象限.
4. B 解析:由题意可知,sin 2α=cos=cos=2×-1=-.
5. A 解析:由题意可知解得m=1,经经验,符合题意.
6. C 解析:由题意知A={x|x2-6x+8<0}={x|2
8. B 解析:因为f(x)在(0,+∞)上单调递减,且f(2)=-log52+1>0,f(3)=-log53<0,所以f(x)=-log5x-x+3的零点所在区间为(2,3).
9. B 解析:设应抽女职工x名,则=,解得x=9.
10. D 解析:由2b+c=2acos C=2a×,则b2+c2-a2=-bc,所以cos A==-.又A∈(0,π),所以A=.
11. B 解析:20组随机数恰好有两个是1,2,3,4的有191,271,932,393,812,184,共6个,因此所求概率为=.
12. A 解析:由题知,不等式x2-4x-a-1≥0对 x∈R恒成立,等价于x∈R时a≤(x2-4x-1)min.因为(x2-4x-1)min=-5,所以a≤-5.
13. B 解析:4sin2α-3sin αcos α-5cos2α=====1.
14. A 解析:因为不等式x2+bx+c<0的解集为(-2,1),所以即不等式cx2+bx+1>0等价于-2x2+x+1>0,解得-
16. A 解析:f(x)=2cos+1=2cos+1,令2x-∈[2kπ,2kπ+π],k∈Z,则x∈,k∈Z,所以函数f(x)的单调减区间为,k∈Z.
17. C 解析:对A,当m=2时,z=0,此时z是实数,故A正确;对B,当m=0时,z=-4i,此时z是纯虚数,故B正确;对C,当m=-2时,z=8,则z+=16,故C错误;对D,当m=1时,z=-1-3i,(-1-3i)2+2(-1-3i)+10=1-9+6i-2-6i+10=0,故D正确.
18. D 解析:若a∥b,b α,则a∥α或a α,故A错误;若a⊥β,a⊥b,b α,则α∥β或α与β相交,故B错误;若a∥α,α⊥β,则a∥β或a β或a与β相交,故C错误;若a⊥α,α⊥β,则a∥β或a β,又由b⊥β,所以a⊥b,故D正确.
19. C 解析:由图可知,f(x)的图象关于原点对称,是奇函数.对于A,D,f(-x)=x2cos x=f(x),f(-x)=x2+cos x=f(x),则函数f(x)=x2cos x,f(x)=x2+cos x是偶函数,排除A和D.当x>0时,f(x)=x+x3>0恒成立,排除B,故选C.
20. A 解析:因为
21. C 解析:由题意,圆柱底面半径r等于球的半径R,圆柱的高h=2R,则V球=πR3,V柱=πr2h=π·R2·2R=2πR3,所以==.
22. D 解析:由题意可知,x1+x2+x3+…+x10=4×10=40,因为s2==
==.
23. D 解析:如图所示,将侧面AA1D1D、侧面CDD1C1延展至同一平面,当A1,M,C三点共线时,A1M+MC取最小值,易知四边形AA1C1C为正方形,则∠CA1C1=45°,且△A1D1M为等腰直角三角形,所以D1M=A1D1=1.在长方体ABCD-A1B1C1D1中,A1M=,因为A1B1⊥平面AA1D1D,A1M 平面AA1D1D,所以A1B1⊥A1M,因此B1M==.
(第23题)
24. D 解析:由向量与的夹角为120°,且||=2,||=3,可得·=6cos 120°=-3.又⊥,所以·=(λ+)·(-)=(λ-1)·+-λ=12-7λ=0,所以λ=.
25. B 解析:因为α∈,β∈(0,π)且α<β,所以α-β∈(-π,0),2α∈(0,π),所以sin(α-β)=-,sin 2α=,所以cos(α+β)=cos[2α-(α-β)]=cos 2αcos(α-β)+sin 2αsin(α-β)=×+×=-.又sin(α+β)=sin[2α-(α-β)]=sin 2αcos(α-β)-cos 2αsin(α-β)=×-×=.因为α+β∈,所以α+β=.
26. A 解析:设g(x)=f(x)-2,x∈R,则g(-x)=3(-x)5+(-x)3+5(-x)=-(3x5+x3+5x)=-g(x),则g(x)为奇函数,且易知g(x)在R上单调递增.又f(a)+f(2a-1)>4可化为f(a)-2>-[f(2a-1)-2] g(a)>-g(2a-1)=g(1-2a),所以a>1-2a,所以a>.
27. D 解析:函数y=ax-1+3(a>0,且a≠1)的图象恒过点P(1,4),则m=1,n=4,则p+4q=1,则+=+=+4≥2+4=6.
28. C 解析:设过滤的次数为n,原来水中杂质为1,则(1-20%)n<5%,即0.8n<,所以lg0.8n
29. 解析:(1) 将数据从小到大排列为:70,74,75,76,80,83,84,85,87,89,91,94,95,96,97,98,100,102,107,117,所以中位数为×(89+91)=90,平均数为×(70+74+75+76+80+83+84+85+87+89+91+94+95+96+97+98+100+102+107+117)=90,极差为117-70=47.
(2) 因为20×80%=16,所以样本数据的第80百分位数是第16、17项数据的平均值,即×(98+100)=99,据此估计每天应进99 kg苹果.
30. 解析:(1)由题知f(-x)=-f(x),则-=-,所以a=1,即f(x)=-.
令x1>x2,则f(x1)-f(x2)=--=-=,又y=2x单调递增,
所以->0,+1>0,+1>0,即f(x1)>f(x2),所以f(x)在R上单调递增.
(2) 由y=2x+1∈(1,+∞),则-∈(-1,0),所以f(x)=-∈.
同课章节目录
