16.1.2 二次根式的性质(2)课件(共15张PPT)
文档属性
| 名称 | 16.1.2 二次根式的性质(2)课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 09:47:50 | ||
图片预览






文档简介
(共15张PPT)
16.1.2 二次根式的性质(2)
1.理解二次根式的性质
2.会运用二次根式的性质进行有关计算和化简.
填空:
_______, _______;
_______, _______;
_______, _______.
-a
2
2
5
5
0
0
a
请比较左右两边的式子,议一议:与有什么关系?
当 a≥0 时,______;当 a<0 时 ,______.
一般地,二次根式有下面的性质:
根据算术平方根的意义,无论 a 是正数、0 或负数, a2 的算术平方根可以记为 .
当 a≥0 时,=a;当 a<0 时,=-a.
而当 a≥0 时, |a|=a;当 a<0 时,|a|=-a.
所以 =|a|.
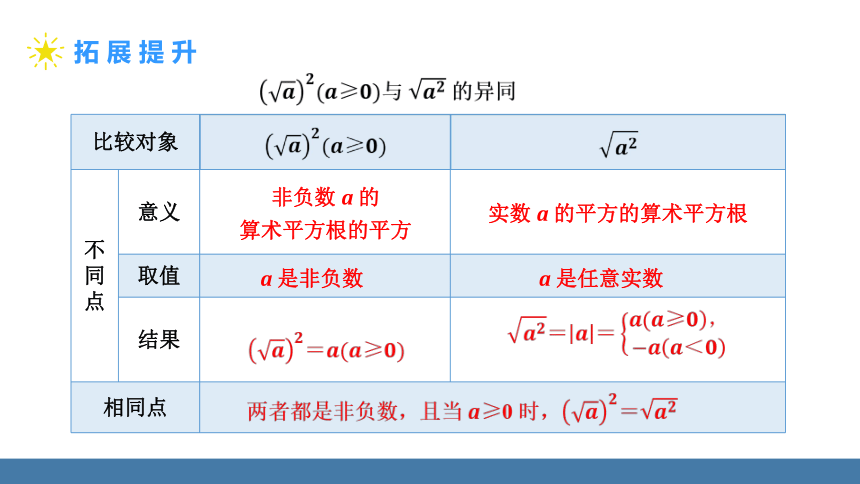
与 的异同
比较对象
不同点 意义
取值
结果
相同点 非负数 a 的
算术平方根的平方
实数 a 的平方的算术平方根
a 是非负数
a 是任意实数
两者都是非负数,且当 a≥0 时,
例1 计算:
(1).
(2).
解:(1)
.
(2)
.
数与二次根式相乘时,乘号可以省略.例如,表示.
例2 计算:.
解: ∵,,
∴原式.
1.定义:用基本运算符号把数或表示数的字母连接起来的式子叫做代数式.
(1)代数式中不能含有“=”“>”“<”“≥”“≤”等关系符号,单独一个数或者字母也是代数式;
(2)将两个代数式用以上关系符号连接起来的式子叫做关系式,等式和不等式都是关系式.
(基本运算包括加、减、乘、除、乘方和开方)
(2)数与字母相乘时,通常把数写在前面.
(3)数字因数是 1 或 -1 时,“1”常省略不写.
(4)带分数与字母相乘时,要将带分数化成假分数.
(5)除法运算通常用分数线.
2.代数式的书写规定:
(1)数与字母相乘或字母与字母相乘时,通常将乘号写作“ · ”或者省略不写.
(1)直接法:根据问题的语言叙述直接写出代数式.
(2)公式法:根据数学相关的公式(面积或体积等)列出代数式.
(3)探究规律法:将蕴含在一组数或一组图形中的规律用代数式表示出来.
3.列代数式的常用方法:
1.(口答)填空:
(1)_______, _______,
_______, _______.
(2)数 a 在数轴上的位置如图,则_______.
-a
1
3
4
2. 计算:
(1).
(2).
解:(1).
(2)
.
3. 用代数式表示:
(1)面积为 S 的圆的半径;
(2)面积为 S 且两条邻边的比为 2∶3 的长方形的长和宽.
解:(1)设圆的半径为 r,则
所以 S=πr ,则 r =±.
又因为圆的半径不能为负数,所以 r =.
解:(2)设长方形的长为 3x,则宽为 2x.
所以 S=3x×2x,则 .
又因为边长不能为负数,
所以 ,长和宽分别为 3,2.
3. 用代数式表示:
(1)面积为 S 的圆的半径;
(2)面积为 S 且两条邻边的比为 2∶3 的长方形的长和宽.
二次
根式
性质
代数式
用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子叫做代数式
16.1.2 二次根式的性质(2)
1.理解二次根式的性质
2.会运用二次根式的性质进行有关计算和化简.
填空:
_______, _______;
_______, _______;
_______, _______.
-a
2
2
5
5
0
0
a
请比较左右两边的式子,议一议:与有什么关系?
当 a≥0 时,______;当 a<0 时 ,______.
一般地,二次根式有下面的性质:
根据算术平方根的意义,无论 a 是正数、0 或负数, a2 的算术平方根可以记为 .
当 a≥0 时,=a;当 a<0 时,=-a.
而当 a≥0 时, |a|=a;当 a<0 时,|a|=-a.
所以 =|a|.
与 的异同
比较对象
不同点 意义
取值
结果
相同点 非负数 a 的
算术平方根的平方
实数 a 的平方的算术平方根
a 是非负数
a 是任意实数
两者都是非负数,且当 a≥0 时,
例1 计算:
(1).
(2).
解:(1)
.
(2)
.
数与二次根式相乘时,乘号可以省略.例如,表示.
例2 计算:.
解: ∵,,
∴原式.
1.定义:用基本运算符号把数或表示数的字母连接起来的式子叫做代数式.
(1)代数式中不能含有“=”“>”“<”“≥”“≤”等关系符号,单独一个数或者字母也是代数式;
(2)将两个代数式用以上关系符号连接起来的式子叫做关系式,等式和不等式都是关系式.
(基本运算包括加、减、乘、除、乘方和开方)
(2)数与字母相乘时,通常把数写在前面.
(3)数字因数是 1 或 -1 时,“1”常省略不写.
(4)带分数与字母相乘时,要将带分数化成假分数.
(5)除法运算通常用分数线.
2.代数式的书写规定:
(1)数与字母相乘或字母与字母相乘时,通常将乘号写作“ · ”或者省略不写.
(1)直接法:根据问题的语言叙述直接写出代数式.
(2)公式法:根据数学相关的公式(面积或体积等)列出代数式.
(3)探究规律法:将蕴含在一组数或一组图形中的规律用代数式表示出来.
3.列代数式的常用方法:
1.(口答)填空:
(1)_______, _______,
_______, _______.
(2)数 a 在数轴上的位置如图,则_______.
-a
1
3
4
2. 计算:
(1).
(2).
解:(1).
(2)
.
3. 用代数式表示:
(1)面积为 S 的圆的半径;
(2)面积为 S 且两条邻边的比为 2∶3 的长方形的长和宽.
解:(1)设圆的半径为 r,则
所以 S=πr ,则 r =±.
又因为圆的半径不能为负数,所以 r =.
解:(2)设长方形的长为 3x,则宽为 2x.
所以 S=3x×2x,则 .
又因为边长不能为负数,
所以 ,长和宽分别为 3,2.
3. 用代数式表示:
(1)面积为 S 的圆的半径;
(2)面积为 S 且两条邻边的比为 2∶3 的长方形的长和宽.
二次
根式
性质
代数式
用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子叫做代数式
