16.3.1 二次根式的加减 课件(共20张PPT)
文档属性
| 名称 | 16.3.1 二次根式的加减 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 09:57:46 | ||
图片预览






文档简介
(共20张PPT)
16.3.1 二次根式的加减
1.能熟练进行二次根式的化简.
2.会识别同类二次根式并进行合并.
3.会利用二次根式的加减法则进行计算.
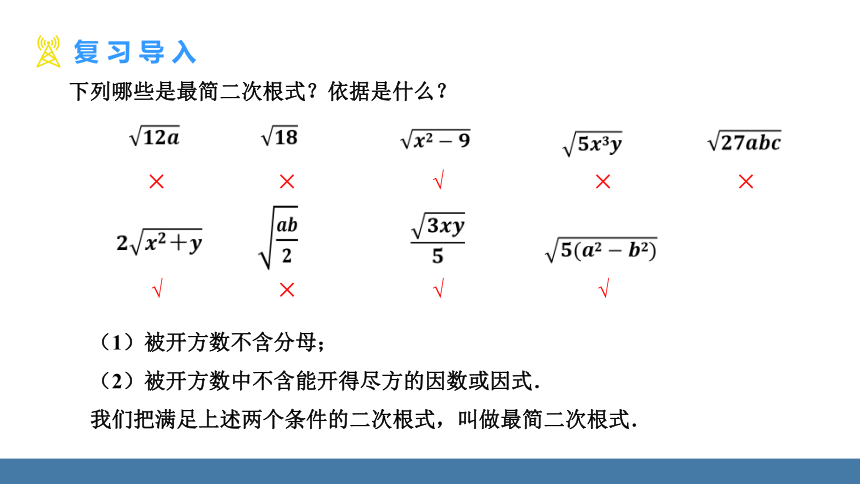
下列哪些是最简二次根式?依据是什么?
√
×
×
×
×
×
√
√
√
我们把满足上述两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
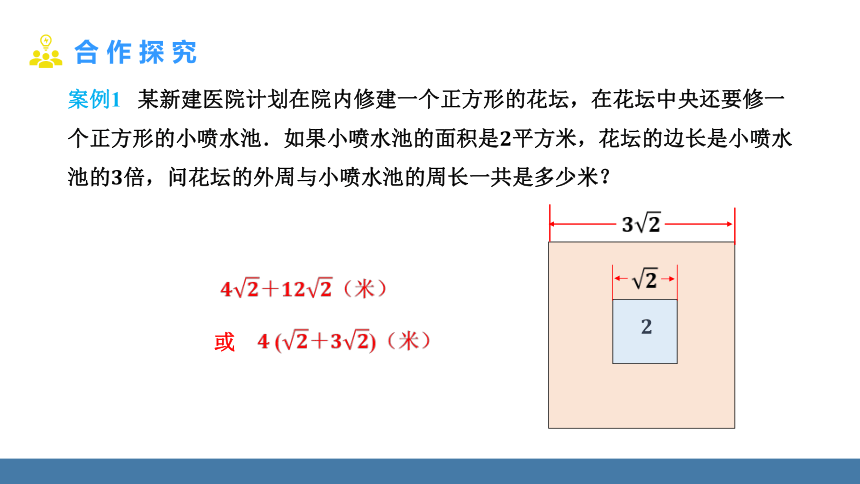
案例1 某新建医院计划在院内修建一个正方形的花坛,在花坛中央还要修一个正方形的小喷水池.如果小喷水池的面积是2平方米,花坛的边长是小喷水池的3倍,问花坛的外周与小喷水池的周长一共是多少米?
2
4+12(米)
4 (+3)(米)
或
8
10
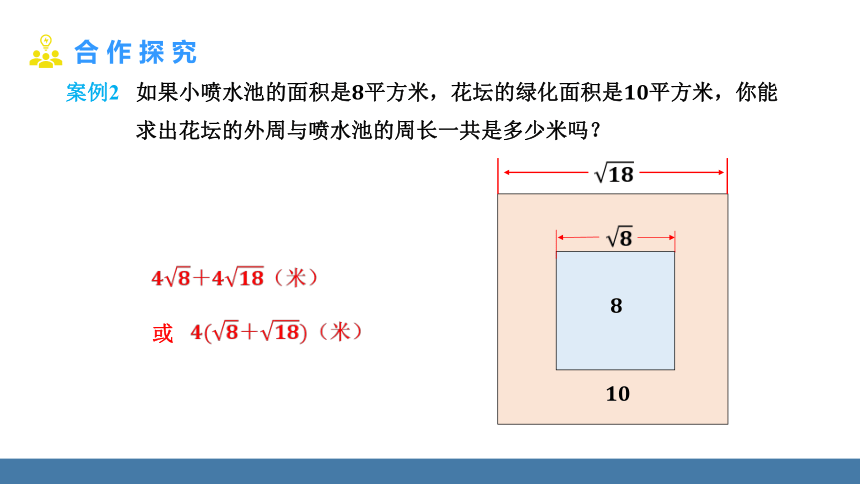
案例2 如果小喷水池的面积是8平方米,花坛的绿化面积是10平方米,你能
求出花坛的外周与喷水池的周长一共是多少米吗?
4+4(米)
4+(米)
或
案例1:
4+12
4 (+3)
或
案例2:
4+4
4 +)
或
2
3
二次根式的加减是如何计算的?
计算:
(1)3x2+2x2=______; (2)x2+2x2+4y=________.
5x2
3x2+4y
4+1
4+ 4
类比合并同类项的方法,下列二次根式能合并吗?
二次根式加减运算的基本方法
结论1: 如果几个二次根式的被开方数相同, 那么可直接根据分配律进行加减运算.
…… (分配律)
4+1
=(4+12)
=16
结论2:如果所给的二次根式不是最简二次根式,应该先化简,再考虑进行加减运算.
……(化为最简二次根式)
……(分配律)
4+ 4
=8+1
=(8+12)
=2
二次根式加减运算的基本方法
注意:被开方数不同的二次根式(如与)不能合并.
判断:下列计算是否正确?为什么?
(1)+ =; (2)2+ =2;
(3) =+ =2+3=5.
二次根式的加减法则
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
×
×
×
同类二次根式
几个二次根式化成_______________以后,如果__________相同,这几个二次根式就叫做同类二次根式 .
最简二次根式
被开方数
判断几个二次根式是同类二次根式的方法:
一是化每个二次根式为最简二次根式;
二是看化简后的二次根式中被开方数是否相同.
思考:(2)中被开方数有小数,该怎样计算?
将被开方数中的小数化为分数,再进行计算.
例1 计算下列各式:
(1)2-3+5; (2)+-(-).
解:2-3+5
= 2-6+15
=11.
解:+-(-)
= 2+-(-)
=2+-+
=-.
计算后根号外的因数是分数的要写成假分数形式,不能写成带分数形式.
例1 计算下列各式:
(1)2-3+5; (2)+-(-).
二次根式加减运算的一般步骤
1.化:将每个二次根式都化成最简二次根式;
2.找:找出被开方数相同的二次根式;
3.合:将被开方数相同的二次根式合并成一项.
例2 计算下列各式:
(1)2-3-; (2)(-10)-3(-).
解:2-3-
= 4--3
= 0.
解:(-10)-3(-)
= 4-10×-3(3-)
= 4-2-9+
= 5-11.
运算 二次根式的乘除 二次根式的加减
系数
被开方数
化简
二次根式的乘除与二次根式的加减的对比
系数相乘除
系数相加减
被开方数相乘除
被开方数不变
结果化为最简
二次根式
先化为最简二次根式,再合并同类二次根式
2.若最简二次根式-2和可以合并,那么a=_____,
b=_____.
D
2
-1
1.下列选项中和是同类二次根式的是( )
A.3 B. C. D.-
3.下列等式中正确的是_______.
①-=; ②5-=5;
③3-2=; ④-=;
⑤-=2; ⑥2+3=5.
⑤
4.计算:
(1)(-3+); (2) +6-2.
解:(-3+)
= (2-+)
=.
解: +6-2
=2+6×-2×.
=2+3-2
=3.
法则
二次根式的乘除与二次根式的加减的对比
二次根式的加减
同类二次根式
一般步骤
化、找、合
16.3.1 二次根式的加减
1.能熟练进行二次根式的化简.
2.会识别同类二次根式并进行合并.
3.会利用二次根式的加减法则进行计算.
下列哪些是最简二次根式?依据是什么?
√
×
×
×
×
×
√
√
√
我们把满足上述两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
案例1 某新建医院计划在院内修建一个正方形的花坛,在花坛中央还要修一个正方形的小喷水池.如果小喷水池的面积是2平方米,花坛的边长是小喷水池的3倍,问花坛的外周与小喷水池的周长一共是多少米?
2
4+12(米)
4 (+3)(米)
或
8
10
案例2 如果小喷水池的面积是8平方米,花坛的绿化面积是10平方米,你能
求出花坛的外周与喷水池的周长一共是多少米吗?
4+4(米)
4+(米)
或
案例1:
4+12
4 (+3)
或
案例2:
4+4
4 +)
或
2
3
二次根式的加减是如何计算的?
计算:
(1)3x2+2x2=______; (2)x2+2x2+4y=________.
5x2
3x2+4y
4+1
4+ 4
类比合并同类项的方法,下列二次根式能合并吗?
二次根式加减运算的基本方法
结论1: 如果几个二次根式的被开方数相同, 那么可直接根据分配律进行加减运算.
…… (分配律)
4+1
=(4+12)
=16
结论2:如果所给的二次根式不是最简二次根式,应该先化简,再考虑进行加减运算.
……(化为最简二次根式)
……(分配律)
4+ 4
=8+1
=(8+12)
=2
二次根式加减运算的基本方法
注意:被开方数不同的二次根式(如与)不能合并.
判断:下列计算是否正确?为什么?
(1)+ =; (2)2+ =2;
(3) =+ =2+3=5.
二次根式的加减法则
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
×
×
×
同类二次根式
几个二次根式化成_______________以后,如果__________相同,这几个二次根式就叫做同类二次根式 .
最简二次根式
被开方数
判断几个二次根式是同类二次根式的方法:
一是化每个二次根式为最简二次根式;
二是看化简后的二次根式中被开方数是否相同.
思考:(2)中被开方数有小数,该怎样计算?
将被开方数中的小数化为分数,再进行计算.
例1 计算下列各式:
(1)2-3+5; (2)+-(-).
解:2-3+5
= 2-6+15
=11.
解:+-(-)
= 2+-(-)
=2+-+
=-.
计算后根号外的因数是分数的要写成假分数形式,不能写成带分数形式.
例1 计算下列各式:
(1)2-3+5; (2)+-(-).
二次根式加减运算的一般步骤
1.化:将每个二次根式都化成最简二次根式;
2.找:找出被开方数相同的二次根式;
3.合:将被开方数相同的二次根式合并成一项.
例2 计算下列各式:
(1)2-3-; (2)(-10)-3(-).
解:2-3-
= 4--3
= 0.
解:(-10)-3(-)
= 4-10×-3(3-)
= 4-2-9+
= 5-11.
运算 二次根式的乘除 二次根式的加减
系数
被开方数
化简
二次根式的乘除与二次根式的加减的对比
系数相乘除
系数相加减
被开方数相乘除
被开方数不变
结果化为最简
二次根式
先化为最简二次根式,再合并同类二次根式
2.若最简二次根式-2和可以合并,那么a=_____,
b=_____.
D
2
-1
1.下列选项中和是同类二次根式的是( )
A.3 B. C. D.-
3.下列等式中正确的是_______.
①-=; ②5-=5;
③3-2=; ④-=;
⑤-=2; ⑥2+3=5.
⑤
4.计算:
(1)(-3+); (2) +6-2.
解:(-3+)
= (2-+)
=.
解: +6-2
=2+6×-2×.
=2+3-2
=3.
法则
二次根式的乘除与二次根式的加减的对比
二次根式的加减
同类二次根式
一般步骤
化、找、合
