17.1.1 勾股定理 课件(共26张PPT)
文档属性
| 名称 | 17.1.1 勾股定理 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 17:24:54 | ||
图片预览



文档简介
(共26张PPT)
第十七章 勾股定理
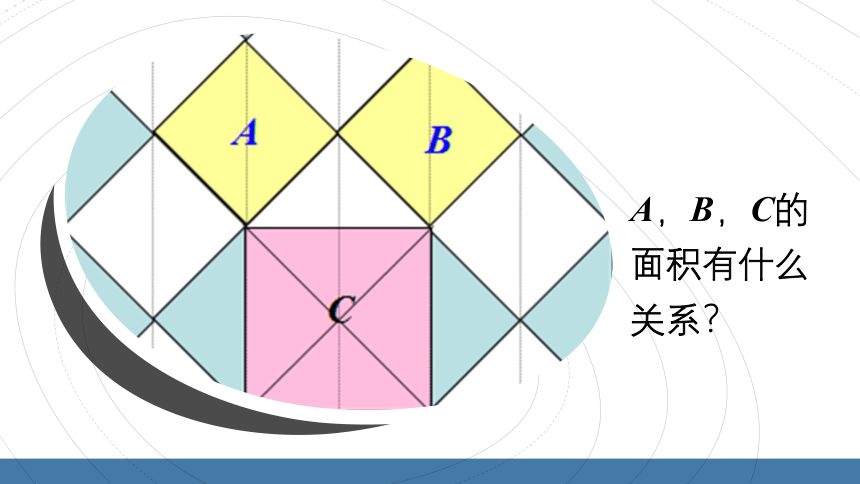
A,B,C的面积有什么关系?
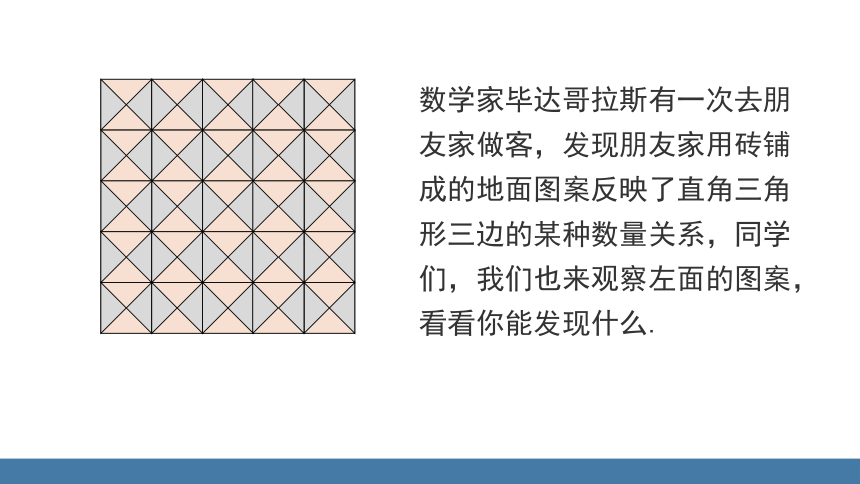
数学家毕达哥拉斯有一次去朋友家做客,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系,同学们,我们也来观察左面的图案,看看你能发现什么.
17.1.1 勾股定理
1.经历勾股定理的探索过程,感受数形结合的思想.
3.尝试用多种方法验证勾股定理,体验解决问题策略的多样性.
2.掌握勾股定理,会运用勾股定理解决一些与直角三角形有关的问题.
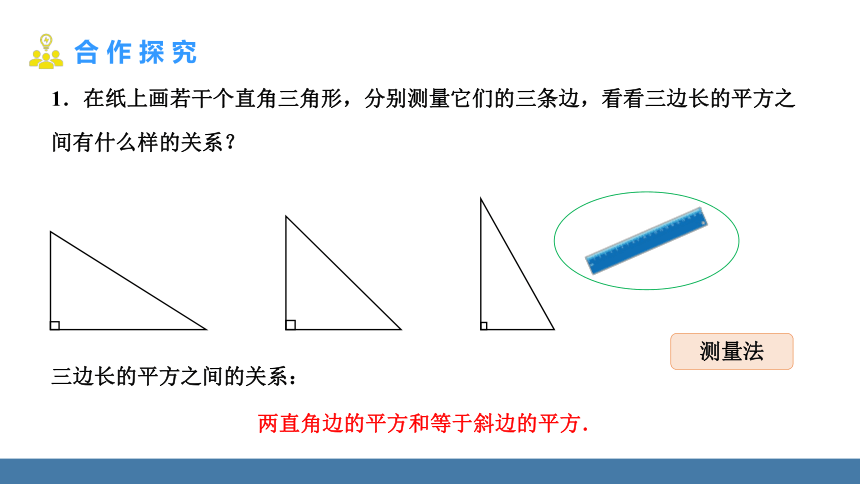
1.在纸上画若干个直角三角形,分别测量它们的三条边,看看三边长的平方之间有什么样的关系?
两直角边的平方和等于斜边的平方.
三边长的平方之间的关系:
测量法
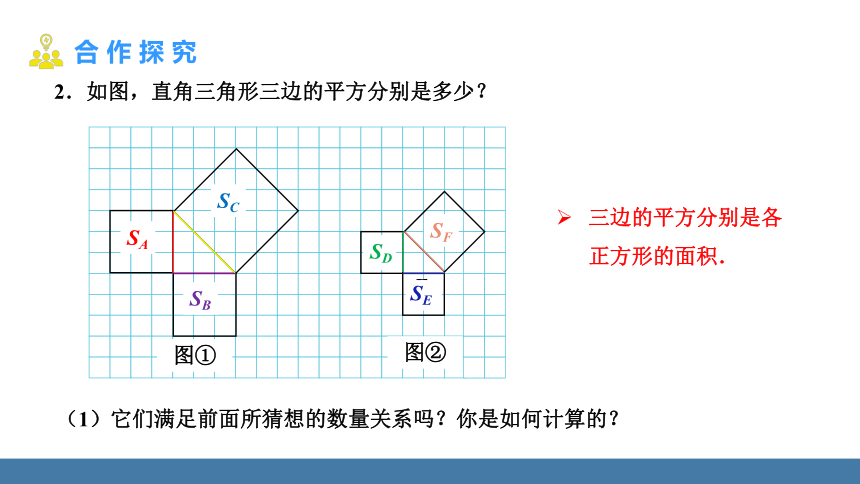
2.如图,直角三角形三边的平方分别是多少?
A
C
B
D
F
E
图①
图②
三边的平方分别是各正方形的面积.
SA
SB
SC
SF
SD
SE
(1)它们满足前面所猜想的数量关系吗?你是如何计算的?
A
C
B
图①
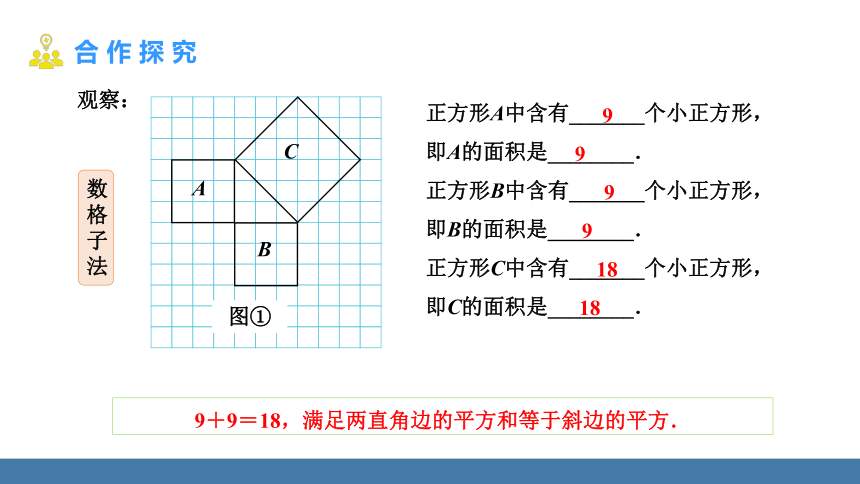
正方形A中含有_______个小正方形,
即A的面积是________.
正方形B中含有_______个小正方形,
即B的面积是________.
正方形C中含有_______个小正方形,
即C的面积是________.
观察:
9
9
9
9
18
18
9+9=18,满足两直角边的平方和等于斜边的平方.
数格子法
D
F
E
图②
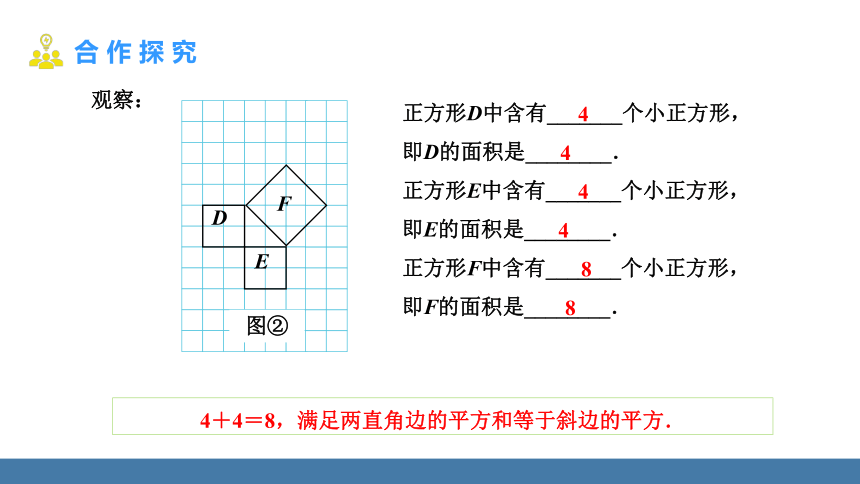
正方形D中含有_______个小正方形,
即D的面积是________.
正方形E中含有_______个小正方形,
即E的面积是________.
正方形F中含有_______个小正方形,
即F的面积是________.
4
4
4
4
8
8
4+4=8,满足两直角边的平方和等于斜边的平方.
观察:
(2)对于下图中的直角三角形,是否还满足前面所猜想的数量关系?你又是如何计算的呢?
A
C
B
图①
正方形C的面积可以
怎么计算呢?
A
C
B
图①
方法一:
分“割”成若干个直角边为整数的三角形
SC=×4×3×4+1×1=25
方法二:
把C“补” 成边长为7的正方形
SC=7×7-×4×3×4=25
正方形A中含有________个小正方形,
即A的面积是_________.
正方形B中含有________个小正方形,
即B的面积是_________.
正方形C中含有________个小正方形,
即C的面积是_________.
16
16
9
9
25
25
16+9=25,满足两直角边的平方和等于斜边的平方.
观察:
A
C
B
图①
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
A
B
C
a
b
c
勾
股
弦
我国古代把直角三角形中
较短的直角边称为勾,
较长的直角边称为股,
斜边称为弦,
“勾股定理”因此而得名.
(在很多国家文献中称为毕达哥拉斯定理)
“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的,右图是弦图的示意图.
c
b
a
黄实
朱实
弦图由四个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形,尝试验证:
a2+b2=c2.
弦图
尝试验证:a2+b2=c2.
化简得:c2 =a2+b2.
S大正方形 =S小正方形+4S直角三角形
c2 =(b-a)2+4·.
这就证明了勾股定理.
证明:
c
b
a
黄实
朱实
弦图
用四个全等的直角三角形,还可以拼成如图所示的图形.与上面的方法类似,根据这一图形,尝试证明勾股定理.
化简得:c2 =a2+b2.
S大正方形=S小正方形+4S直角三角形
(b+a)2 = c2+4·.
证明:
c
b
a
a
b
a
a
b
c
c
c
b
解:(1)∵a2+b2=c2,即 62+b2=102,
又 b>0,∴ b=8.
例1 设直角三角形的两条直角边长分别为 a 和 b,斜边长为 c.
(1)已知 a=6,c=10,求 b;
(2)已知 a=5,b=12,求 c;
(3)已知 c=25,b=15,求 a.
解:(2)∵ a2+b2=c2,即 52+122=c2,
又 c>0,∴c=13.
例1 设直角三角形的两条直角边长分别为 a 和 b,斜边长为 c.
(1)已知 a=6,c=10,求 b;
(2)已知 a=5,b=12,求 c;
(3)已知 c=25,b=15,求 a.
解:(3)∵ a2+b2=c2,即 a2+152=252,
又 a>0,∴ a=20.
首先分清斜边和直角边,然后利用“直角三角形两直角边的平方和等于斜边的平方”即可求出未知边的长.
例1 设直角三角形的两条直角边长分别为 a 和 b,斜边长为 c.
(1)已知 a=6,c=10,求 b;
(2)已知 a=5,b=12,求 c;
(3)已知 c=25,b=15,求 a.
例2 如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方
形 A,B,C,D 的边长分别是 12,16,9,12,求最大正方形E的面积.
解:由图形可知,正方形 E 的边长为
=25,
故E的面积为 252=625.
通过三个直角三角形,明确已知的正方形边长和未知的正方形边长之间的关系,从而得到所求正方形的边长,即可得到所求正方形的面积.
1.求下图中字母所代表的正方形的面积.
SA=225+400=625
225
400
A
81
225
B
SB=225-81=144
2.求斜边长17 cm,一条直角边长15 cm的直角三角形的面积.
15
17
A
C
B
解:∵三角形是直角三角形,
∴BC2 =AB2-AC2
=172-152
=64,
∴BC=8.
∴S△ABC=×AC×BC=×15×8=60(cm2).
D
C
B
A
5 cm
5 cm
6 cm
3.如图,求等腰△ABC的面积.
解:作AD⊥BC.
∵△ABC是等腰三角形,
∴BD=DC=3 cm,
在直角三角形ABD中,AD2=AB2-BD2=16,
∴AD=4 cm.
∴S△ABC=×AD×BC=×4×6=12(cm2).
勾股定理
证明
定理
a2+b2=c2
赵爽弦图
第十七章 勾股定理
A,B,C的面积有什么关系?
数学家毕达哥拉斯有一次去朋友家做客,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系,同学们,我们也来观察左面的图案,看看你能发现什么.
17.1.1 勾股定理
1.经历勾股定理的探索过程,感受数形结合的思想.
3.尝试用多种方法验证勾股定理,体验解决问题策略的多样性.
2.掌握勾股定理,会运用勾股定理解决一些与直角三角形有关的问题.
1.在纸上画若干个直角三角形,分别测量它们的三条边,看看三边长的平方之间有什么样的关系?
两直角边的平方和等于斜边的平方.
三边长的平方之间的关系:
测量法
2.如图,直角三角形三边的平方分别是多少?
A
C
B
D
F
E
图①
图②
三边的平方分别是各正方形的面积.
SA
SB
SC
SF
SD
SE
(1)它们满足前面所猜想的数量关系吗?你是如何计算的?
A
C
B
图①
正方形A中含有_______个小正方形,
即A的面积是________.
正方形B中含有_______个小正方形,
即B的面积是________.
正方形C中含有_______个小正方形,
即C的面积是________.
观察:
9
9
9
9
18
18
9+9=18,满足两直角边的平方和等于斜边的平方.
数格子法
D
F
E
图②
正方形D中含有_______个小正方形,
即D的面积是________.
正方形E中含有_______个小正方形,
即E的面积是________.
正方形F中含有_______个小正方形,
即F的面积是________.
4
4
4
4
8
8
4+4=8,满足两直角边的平方和等于斜边的平方.
观察:
(2)对于下图中的直角三角形,是否还满足前面所猜想的数量关系?你又是如何计算的呢?
A
C
B
图①
正方形C的面积可以
怎么计算呢?
A
C
B
图①
方法一:
分“割”成若干个直角边为整数的三角形
SC=×4×3×4+1×1=25
方法二:
把C“补” 成边长为7的正方形
SC=7×7-×4×3×4=25
正方形A中含有________个小正方形,
即A的面积是_________.
正方形B中含有________个小正方形,
即B的面积是_________.
正方形C中含有________个小正方形,
即C的面积是_________.
16
16
9
9
25
25
16+9=25,满足两直角边的平方和等于斜边的平方.
观察:
A
C
B
图①
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
A
B
C
a
b
c
勾
股
弦
我国古代把直角三角形中
较短的直角边称为勾,
较长的直角边称为股,
斜边称为弦,
“勾股定理”因此而得名.
(在很多国家文献中称为毕达哥拉斯定理)
“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的,右图是弦图的示意图.
c
b
a
黄实
朱实
弦图由四个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形,尝试验证:
a2+b2=c2.
弦图
尝试验证:a2+b2=c2.
化简得:c2 =a2+b2.
S大正方形 =S小正方形+4S直角三角形
c2 =(b-a)2+4·.
这就证明了勾股定理.
证明:
c
b
a
黄实
朱实
弦图
用四个全等的直角三角形,还可以拼成如图所示的图形.与上面的方法类似,根据这一图形,尝试证明勾股定理.
化简得:c2 =a2+b2.
S大正方形=S小正方形+4S直角三角形
(b+a)2 = c2+4·.
证明:
c
b
a
a
b
a
a
b
c
c
c
b
解:(1)∵a2+b2=c2,即 62+b2=102,
又 b>0,∴ b=8.
例1 设直角三角形的两条直角边长分别为 a 和 b,斜边长为 c.
(1)已知 a=6,c=10,求 b;
(2)已知 a=5,b=12,求 c;
(3)已知 c=25,b=15,求 a.
解:(2)∵ a2+b2=c2,即 52+122=c2,
又 c>0,∴c=13.
例1 设直角三角形的两条直角边长分别为 a 和 b,斜边长为 c.
(1)已知 a=6,c=10,求 b;
(2)已知 a=5,b=12,求 c;
(3)已知 c=25,b=15,求 a.
解:(3)∵ a2+b2=c2,即 a2+152=252,
又 a>0,∴ a=20.
首先分清斜边和直角边,然后利用“直角三角形两直角边的平方和等于斜边的平方”即可求出未知边的长.
例1 设直角三角形的两条直角边长分别为 a 和 b,斜边长为 c.
(1)已知 a=6,c=10,求 b;
(2)已知 a=5,b=12,求 c;
(3)已知 c=25,b=15,求 a.
例2 如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方
形 A,B,C,D 的边长分别是 12,16,9,12,求最大正方形E的面积.
解:由图形可知,正方形 E 的边长为
=25,
故E的面积为 252=625.
通过三个直角三角形,明确已知的正方形边长和未知的正方形边长之间的关系,从而得到所求正方形的边长,即可得到所求正方形的面积.
1.求下图中字母所代表的正方形的面积.
SA=225+400=625
225
400
A
81
225
B
SB=225-81=144
2.求斜边长17 cm,一条直角边长15 cm的直角三角形的面积.
15
17
A
C
B
解:∵三角形是直角三角形,
∴BC2 =AB2-AC2
=172-152
=64,
∴BC=8.
∴S△ABC=×AC×BC=×15×8=60(cm2).
D
C
B
A
5 cm
5 cm
6 cm
3.如图,求等腰△ABC的面积.
解:作AD⊥BC.
∵△ABC是等腰三角形,
∴BD=DC=3 cm,
在直角三角形ABD中,AD2=AB2-BD2=16,
∴AD=4 cm.
∴S△ABC=×AD×BC=×4×6=12(cm2).
勾股定理
证明
定理
a2+b2=c2
赵爽弦图
