17.1.2 勾股定理的应用 课件(共21张PPT)
文档属性
| 名称 | 17.1.2 勾股定理的应用 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 17:26:52 | ||
图片预览







文档简介
(共21张PPT)
17.1.2 勾股定理的应用
1.学会利用勾股定理的数学思想解决生活中的实际问题.
2.能熟练将实际问题转化为数学模型进行计算.
波平如镜一湖面,半尺高处出红莲.
婷婷多姿湖中立,突遭狂风吹一边.
离开原处两尺远,花贴湖边似睡莲.
请你动动脑筋看,湖水在此多深浅.
这节课我们就来学习用勾股定理来解决这一实际问题.
印度的数学家婆神迦罗在他的著作《丽拉瓦提》中提出这样一个问题:
上面的问题可以归结为:如图,AC 长为 0.5 尺,BC 长为 2 尺,OA=OB,求 OC 长为几尺.请你解答这个问题.
A
C
O
B
解:OA=OB=OC+0.5,
在 Rt△OBC 中,根据勾股定理,
OB2=OC2+BC2,
即 (OC+0.5)2=OC2+22,
OC=3.75.
所以 OC 长为 3.75 尺.
应用勾股定理解决实际问题,关键是将实际问题转化为直角三角形模型.
如图,有一个圆柱,它的高等于12 cm,底面圆的周长为18 cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是多少?
A
B
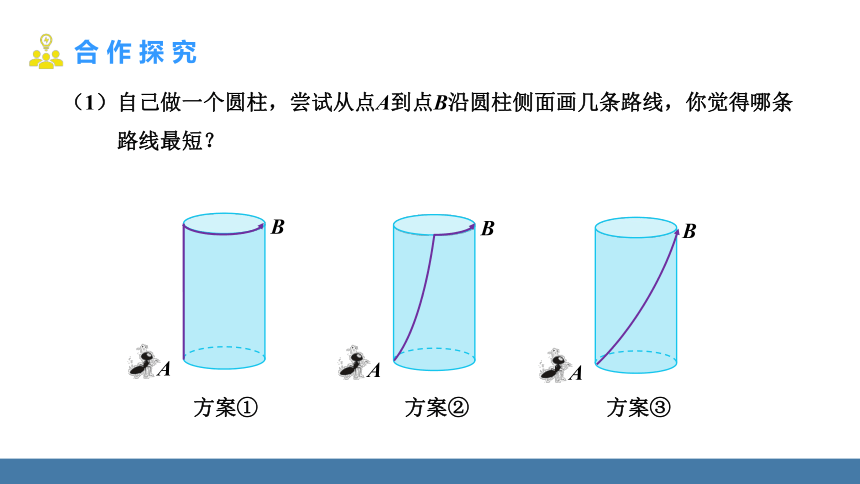
(1)自己做一个圆柱,尝试从点A到点B沿圆柱侧面画几条路线,你觉得哪条
路线最短?
A
B
A
B
A
B
方案①
方案②
方案③
(2)如图,将圆柱侧面剪开展成一个长方形,点A到点B的最短路线是什么?
你画对了吗?
A
B
A
B
A
B
∵两点之间线段最短,
∴方案③的路线最短.
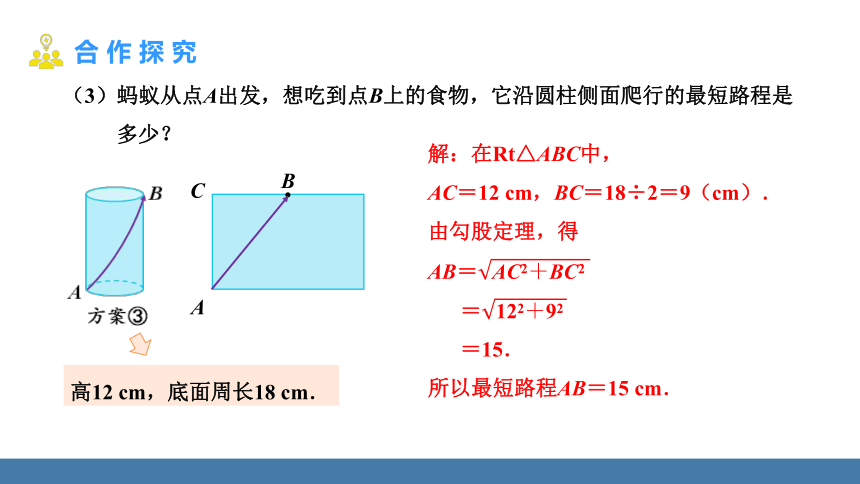
(3)蚂蚁从点A出发,想吃到点B上的食物,它沿圆柱侧面爬行的最短路程是
多少?
解:在Rt△ABC中,
AC=12 cm,BC=18÷2=9(cm).
由勾股定理,得
AB=
=
=15.
所以最短路程AB=15 cm.
A
B
C
高12 cm,底面周长18 cm.
求立体图形中最短路径问题的一般步骤:
(1)展平:将立体图形表面展开为平面图形,只需展开包含相关点的面(可能存在多种展法).
(2)定点:确定相关点的位置.
(3)连线:连接相关点,构造直角三角形.
(4)计算:利用勾股定理求解.
例1 如图,一高层住宅发生火灾,消防车立即赶到距住宅楼8 m(车尾AE距住宅楼墙面CD)处,升起云梯到火灾窗口B.已知云梯AB长17 m,云梯底部距地面的高AE=1.5 m,问发生火灾的住户窗口距离地面多高?
解:∵AC⊥BC,
∴∠ACB=90°.
根据勾股定理,得BC2=172-82=152(m),
∴BC=15 m.
∴BD=15+1.5=16.5(m).
答:发生火灾的住户窗口距离地面16.5 m.
例2 有一个圆柱形油罐,要从A点环绕油罐建梯子,正好建到A点的正上方B
点,问梯子最短需多少米?(已知:油罐的底面半径是2 m,高AB是5 m,
π取3)
A
B
A
B
A′
B′
解:圆柱形油罐的展开图如图,
则AB′为梯子的最短距离.
AA′=2πr=2×3×2=12(m),
A′B′=5 m,
由勾股定理,得
AB′ 2= AA′ 2 + A′B′ 2
=122+52
=169.
所以AB′=13.
即梯子最短需13 m.
A
B
展开
利用勾股定理解应用题的三步骤
1
2
3
根据题意,画出图形
分析题目中的数量关系,数形结合,正确标图,将已知条件体现到图形中
在适当的直角三角形中应用勾股定理进行计算或建立等量关系,列出方程,解决问题
勾股定理应用的常见类型
1.已知直角三角形的任意两边求第三边;
2.已知直角三角形的任意一边确定另两边的关系;
3.证明包含有平方(算术平方根)关系的几何问题;
4.求解几何体表面上的最短路径问题;
5.构造方程(或方程组)计算有关线段长度,解决生产、
生活中的实际问题.
1.如图,一只蚂蚁从长、宽都是3 cm ,高是8 cm的长方体纸箱的A点沿纸箱
爬到B点,那么它所爬行的最短路线的长是( )
A.(3+8)cm
B.10 cm
C.14 cm
D.无法确定
A
B
B
2.有两棵树,一棵高10 m,另一棵高4 m,两树相距8 m.一只小鸟从一棵树
的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
A.8 m B.10 m C.12 m D.14 m
3.小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1 m,当
他把绳子下端拉开5 m后,发现下端刚好接触地面,则旗杆高度为_____m.
B
12
4.如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在
花园内走出了一条“路”,仅仅少走了______步路,却踩伤了花草.(假
设1米为2步)
A
B
C
4 m
3 m
“路”
4
5. 一辆装满货物的卡车,其外形高2.5 m,宽1.6 m,要开进厂门形状如图所示
的某工厂(上方半圆,下方长方形) ,问这辆卡车能否通过该工厂的厂门.
A
B
2.3 m
2 m
解:∵车宽1.6 m,
∴卡车能否通过,只要比较距厂门中线0.8 m处的门高与车高.
如图所示,点O为AB中点,点D在离厂门中线0.8 m处,且
CD⊥AB,与地面交于H.
在Rt△OCD中,由勾股定理可得:
CD===0.6(m),
CH=CD+DH=0.6+2.3=2.9>2.5,
∴卡车能通过此门.
A
B
2.3 m
2 m
O
D
C
H
勾股定理的应用
实际问题
数学问题
勾股定理
直角三角形
转化
构建
运用
解决
17.1.2 勾股定理的应用
1.学会利用勾股定理的数学思想解决生活中的实际问题.
2.能熟练将实际问题转化为数学模型进行计算.
波平如镜一湖面,半尺高处出红莲.
婷婷多姿湖中立,突遭狂风吹一边.
离开原处两尺远,花贴湖边似睡莲.
请你动动脑筋看,湖水在此多深浅.
这节课我们就来学习用勾股定理来解决这一实际问题.
印度的数学家婆神迦罗在他的著作《丽拉瓦提》中提出这样一个问题:
上面的问题可以归结为:如图,AC 长为 0.5 尺,BC 长为 2 尺,OA=OB,求 OC 长为几尺.请你解答这个问题.
A
C
O
B
解:OA=OB=OC+0.5,
在 Rt△OBC 中,根据勾股定理,
OB2=OC2+BC2,
即 (OC+0.5)2=OC2+22,
OC=3.75.
所以 OC 长为 3.75 尺.
应用勾股定理解决实际问题,关键是将实际问题转化为直角三角形模型.
如图,有一个圆柱,它的高等于12 cm,底面圆的周长为18 cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是多少?
A
B
(1)自己做一个圆柱,尝试从点A到点B沿圆柱侧面画几条路线,你觉得哪条
路线最短?
A
B
A
B
A
B
方案①
方案②
方案③
(2)如图,将圆柱侧面剪开展成一个长方形,点A到点B的最短路线是什么?
你画对了吗?
A
B
A
B
A
B
∵两点之间线段最短,
∴方案③的路线最短.
(3)蚂蚁从点A出发,想吃到点B上的食物,它沿圆柱侧面爬行的最短路程是
多少?
解:在Rt△ABC中,
AC=12 cm,BC=18÷2=9(cm).
由勾股定理,得
AB=
=
=15.
所以最短路程AB=15 cm.
A
B
C
高12 cm,底面周长18 cm.
求立体图形中最短路径问题的一般步骤:
(1)展平:将立体图形表面展开为平面图形,只需展开包含相关点的面(可能存在多种展法).
(2)定点:确定相关点的位置.
(3)连线:连接相关点,构造直角三角形.
(4)计算:利用勾股定理求解.
例1 如图,一高层住宅发生火灾,消防车立即赶到距住宅楼8 m(车尾AE距住宅楼墙面CD)处,升起云梯到火灾窗口B.已知云梯AB长17 m,云梯底部距地面的高AE=1.5 m,问发生火灾的住户窗口距离地面多高?
解:∵AC⊥BC,
∴∠ACB=90°.
根据勾股定理,得BC2=172-82=152(m),
∴BC=15 m.
∴BD=15+1.5=16.5(m).
答:发生火灾的住户窗口距离地面16.5 m.
例2 有一个圆柱形油罐,要从A点环绕油罐建梯子,正好建到A点的正上方B
点,问梯子最短需多少米?(已知:油罐的底面半径是2 m,高AB是5 m,
π取3)
A
B
A
B
A′
B′
解:圆柱形油罐的展开图如图,
则AB′为梯子的最短距离.
AA′=2πr=2×3×2=12(m),
A′B′=5 m,
由勾股定理,得
AB′ 2= AA′ 2 + A′B′ 2
=122+52
=169.
所以AB′=13.
即梯子最短需13 m.
A
B
展开
利用勾股定理解应用题的三步骤
1
2
3
根据题意,画出图形
分析题目中的数量关系,数形结合,正确标图,将已知条件体现到图形中
在适当的直角三角形中应用勾股定理进行计算或建立等量关系,列出方程,解决问题
勾股定理应用的常见类型
1.已知直角三角形的任意两边求第三边;
2.已知直角三角形的任意一边确定另两边的关系;
3.证明包含有平方(算术平方根)关系的几何问题;
4.求解几何体表面上的最短路径问题;
5.构造方程(或方程组)计算有关线段长度,解决生产、
生活中的实际问题.
1.如图,一只蚂蚁从长、宽都是3 cm ,高是8 cm的长方体纸箱的A点沿纸箱
爬到B点,那么它所爬行的最短路线的长是( )
A.(3+8)cm
B.10 cm
C.14 cm
D.无法确定
A
B
B
2.有两棵树,一棵高10 m,另一棵高4 m,两树相距8 m.一只小鸟从一棵树
的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
A.8 m B.10 m C.12 m D.14 m
3.小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1 m,当
他把绳子下端拉开5 m后,发现下端刚好接触地面,则旗杆高度为_____m.
B
12
4.如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在
花园内走出了一条“路”,仅仅少走了______步路,却踩伤了花草.(假
设1米为2步)
A
B
C
4 m
3 m
“路”
4
5. 一辆装满货物的卡车,其外形高2.5 m,宽1.6 m,要开进厂门形状如图所示
的某工厂(上方半圆,下方长方形) ,问这辆卡车能否通过该工厂的厂门.
A
B
2.3 m
2 m
解:∵车宽1.6 m,
∴卡车能否通过,只要比较距厂门中线0.8 m处的门高与车高.
如图所示,点O为AB中点,点D在离厂门中线0.8 m处,且
CD⊥AB,与地面交于H.
在Rt△OCD中,由勾股定理可得:
CD===0.6(m),
CH=CD+DH=0.6+2.3=2.9>2.5,
∴卡车能通过此门.
A
B
2.3 m
2 m
O
D
C
H
勾股定理的应用
实际问题
数学问题
勾股定理
直角三角形
转化
构建
运用
解决
