18.1.1.2 平行四边形对角线的性质 课件(共15张PPT)
文档属性
| 名称 | 18.1.1.2 平行四边形对角线的性质 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 957.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 17:41:28 | ||
图片预览




文档简介
(共15张PPT)
18.1.1.2 平行四边形对角线的性质
1.理解并掌握平行四边形的对角线互相平分的性质.
2.根据平行四边形的性质进行简单的计算和证明.
什么是平行四边形?
两组对边分别平行的四边形叫做平行四边形.
上节课我们学行四边形的哪些性质?
平行四边形是中心对称图形,它的对称中心是两条对角线的交点.
平行四边形的对边相等;平行四边形的对角相等.
平行四边形还有其他性质吗?
很久以前,一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
你认为老人这样分合理吗?为什么?
老大
老二
老三
老四
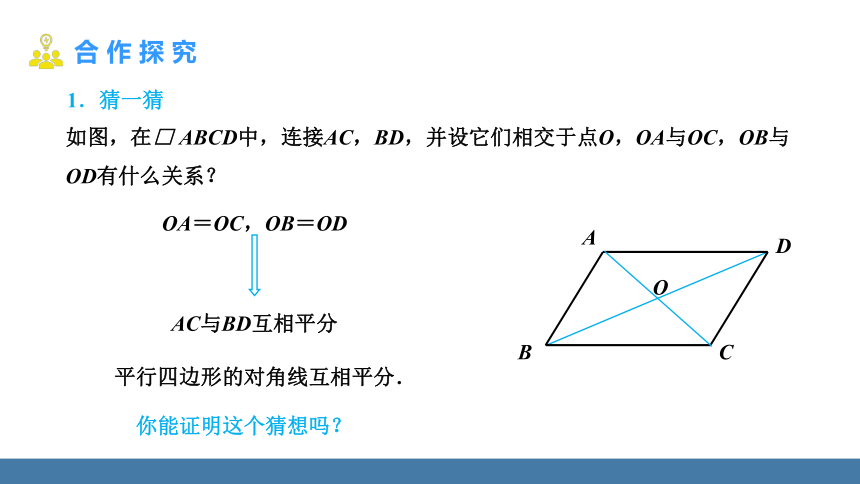
如图,在□ ABCD中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?
平行四边形的对角线互相平分.
你能证明这个猜想吗?
OA=OC,OB=OD
AC与BD互相平分
1.猜一猜
A
D
B
C
O
A
C
D
B
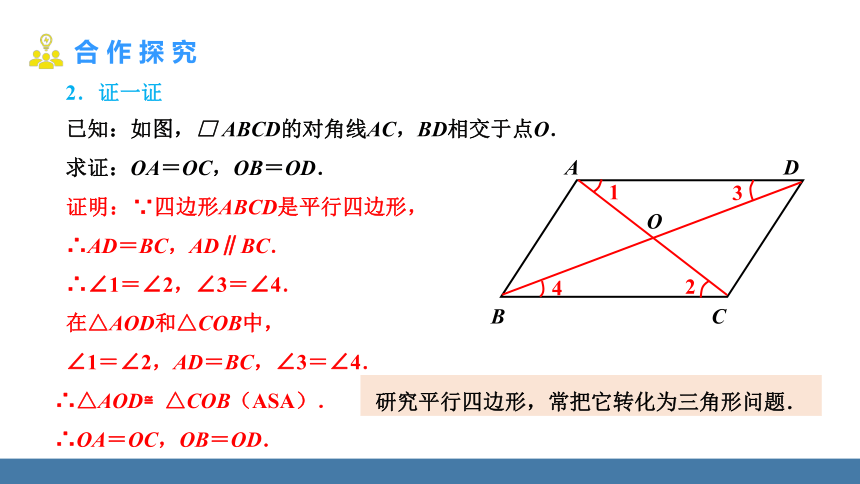
已知:如图,□ ABCD的对角线AC,BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∴∠1=∠2,∠3=∠4.
∴△AOD≌△COB(ASA).
∴OA=OC,OB=OD.
3
2
4
1
在△AOD和△COB中,
∠1=∠2,AD=BC,∠3=∠4.
研究平行四边形,常把它转化为三角形问题.
O
2.证一证
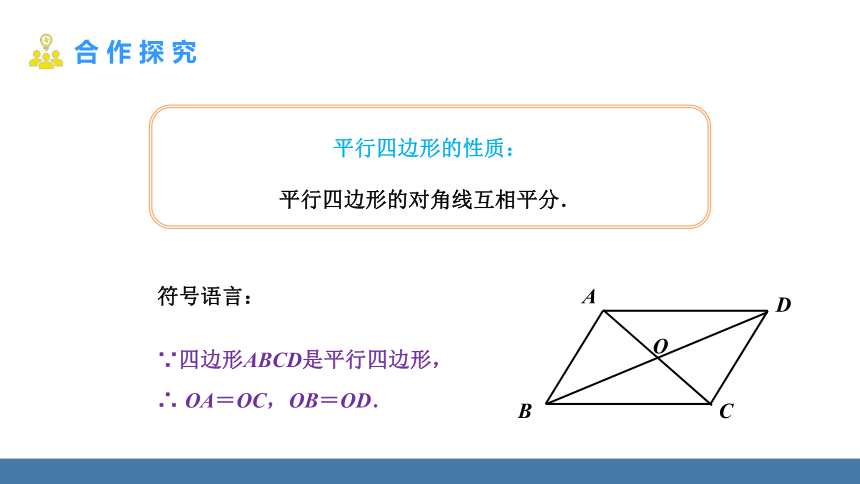
平行四边形的性质:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形,
OA=OC,
OB=OD.
∴
A
D
B
C
O
研究对象 研究结果 几何表示
对边
对角
邻角
对角线
平行四边形的性质
平行
且相等
相等
互补
∠BAD=∠BCD,∠ABC=∠ADC
AB∥CD,AD∥BC
=
=
例如,∠BAD+∠ABC=180°
互相平分
AO=CO,BO=DO
O
B
A
C
D
平行四边形的对角线将平行四边形分成四个面积相等的三角形,都等于平行四边形面积的四分之一.
所以S△ABO=S△ADO.同理S△ABO=S△ADO=S△CBO=S△CDO .
老人分地合理吗?
老人分地合理
理由:过点A作AE⊥BD于点E,
因为四边形ABCD是平行四边形,
所以BO=DO.
S△ABO=
S△ADO=
所以
老大
老二
老三
老四
A
D
B
C
O
E
例1 如图,O为□ ABCD两条对角线的交点,AC=24 mm,
BD=38 mm,BC=28 mm.求△OAD的周长.
C
A
B
O
●
D
解:在□ ABCD中,
∵AC=24 mm,BD=38 mm,
∴AO=AC=12(mm),
DO=BD=19(mm).
又∵BC=28 mm,
∴AD=BC=28(mm),
∴△OAD的周长= AO+DO+AD
=12+19+28=59(mm).
例2 如图,平行四边形ABCD的对角线AC与BD相交于点O,直线EF过点 O与 AD,BC分别相交于点E,F.
求证: OE=OF,AE=CF,DE=BF.
C
A
E
O
●
B
D
证明:∵四边形ABCD是平行四边形,且对角线AC与BD相交于点O,
∴OA=OC,∠EAO=∠FCO,
又∵∠AOE=∠COF,
∴△ AOE ≌△COF .
∴OE=OF,AE=CF.
F
又∵ AD=BC,
∴DE=AD-AE=CB-CF=BF.
1.如图,平行四边形ABCD的对角线AC,BD相交于点O,若AD=16,AC=24,BD=18,则△OBC的周长为( )
A.26 B.37 C.40 D.52
B
分析: △OBC的周长= BC+CO+OB,根据平行四边形的对角线互相平分,对边相等,即可求得答案.
解析:∵AC=10,BD=8,
∴OA=AC=5,OD=BD=4,
∴5-4<AD<5+4,
即1<AD<9.
2.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AC=10,BD=8,则AD的取值范围是______________.
A
B
O
D
C
1<AD<9
3.如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别为OA,OC的中点.求证:△OBE≌△ODF .
A
O
C
F
E
B
D
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别为OA,OC的中点,
∴OE=OA,OF=OC,
即OE=OF,
又∵∠BOE=∠DOF,
∴△OBE≌△ODF .
平行四边形的性质
对称性
对边、对角的性质
对角线的性质
平行四边形是中心对称图形,
两条对角线的交点是它的对称中心
平行四边形的对边相等、
对角相等
平行四边形的对角线互相
平分
18.1.1.2 平行四边形对角线的性质
1.理解并掌握平行四边形的对角线互相平分的性质.
2.根据平行四边形的性质进行简单的计算和证明.
什么是平行四边形?
两组对边分别平行的四边形叫做平行四边形.
上节课我们学行四边形的哪些性质?
平行四边形是中心对称图形,它的对称中心是两条对角线的交点.
平行四边形的对边相等;平行四边形的对角相等.
平行四边形还有其他性质吗?
很久以前,一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
你认为老人这样分合理吗?为什么?
老大
老二
老三
老四
如图,在□ ABCD中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?
平行四边形的对角线互相平分.
你能证明这个猜想吗?
OA=OC,OB=OD
AC与BD互相平分
1.猜一猜
A
D
B
C
O
A
C
D
B
已知:如图,□ ABCD的对角线AC,BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∴∠1=∠2,∠3=∠4.
∴△AOD≌△COB(ASA).
∴OA=OC,OB=OD.
3
2
4
1
在△AOD和△COB中,
∠1=∠2,AD=BC,∠3=∠4.
研究平行四边形,常把它转化为三角形问题.
O
2.证一证
平行四边形的性质:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形,
OA=OC,
OB=OD.
∴
A
D
B
C
O
研究对象 研究结果 几何表示
对边
对角
邻角
对角线
平行四边形的性质
平行
且相等
相等
互补
∠BAD=∠BCD,∠ABC=∠ADC
AB∥CD,AD∥BC
=
=
例如,∠BAD+∠ABC=180°
互相平分
AO=CO,BO=DO
O
B
A
C
D
平行四边形的对角线将平行四边形分成四个面积相等的三角形,都等于平行四边形面积的四分之一.
所以S△ABO=S△ADO.同理S△ABO=S△ADO=S△CBO=S△CDO .
老人分地合理吗?
老人分地合理
理由:过点A作AE⊥BD于点E,
因为四边形ABCD是平行四边形,
所以BO=DO.
S△ABO=
S△ADO=
所以
老大
老二
老三
老四
A
D
B
C
O
E
例1 如图,O为□ ABCD两条对角线的交点,AC=24 mm,
BD=38 mm,BC=28 mm.求△OAD的周长.
C
A
B
O
●
D
解:在□ ABCD中,
∵AC=24 mm,BD=38 mm,
∴AO=AC=12(mm),
DO=BD=19(mm).
又∵BC=28 mm,
∴AD=BC=28(mm),
∴△OAD的周长= AO+DO+AD
=12+19+28=59(mm).
例2 如图,平行四边形ABCD的对角线AC与BD相交于点O,直线EF过点 O与 AD,BC分别相交于点E,F.
求证: OE=OF,AE=CF,DE=BF.
C
A
E
O
●
B
D
证明:∵四边形ABCD是平行四边形,且对角线AC与BD相交于点O,
∴OA=OC,∠EAO=∠FCO,
又∵∠AOE=∠COF,
∴△ AOE ≌△COF .
∴OE=OF,AE=CF.
F
又∵ AD=BC,
∴DE=AD-AE=CB-CF=BF.
1.如图,平行四边形ABCD的对角线AC,BD相交于点O,若AD=16,AC=24,BD=18,则△OBC的周长为( )
A.26 B.37 C.40 D.52
B
分析: △OBC的周长= BC+CO+OB,根据平行四边形的对角线互相平分,对边相等,即可求得答案.
解析:∵AC=10,BD=8,
∴OA=AC=5,OD=BD=4,
∴5-4<AD<5+4,
即1<AD<9.
2.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AC=10,BD=8,则AD的取值范围是______________.
A
B
O
D
C
1<AD<9
3.如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别为OA,OC的中点.求证:△OBE≌△ODF .
A
O
C
F
E
B
D
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别为OA,OC的中点,
∴OE=OA,OF=OC,
即OE=OF,
又∵∠BOE=∠DOF,
∴△OBE≌△ODF .
平行四边形的性质
对称性
对边、对角的性质
对角线的性质
平行四边形是中心对称图形,
两条对角线的交点是它的对称中心
平行四边形的对边相等、
对角相等
平行四边形的对角线互相
平分
