18.1.2.1 平行四边形的判定(2) 课件(共16张PPT)
文档属性
| 名称 | 18.1.2.1 平行四边形的判定(2) 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 858.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 17:45:35 | ||
图片预览






文档简介
(共16张PPT)
18.1.2.1 平行四边形的判定(2)
1.探索并证明平行四边形的判定方法.
2.能熟练运用平行四边形的判定方法去计算和证明.
1.两组对边分别 的四边形是平行四边形.
2.两组对角分别 的四边形是平行四边形.
3.对角线 的四边形是平行四边形.
4.定义法:两组对边分别______的四边形是平行四边形.
相等
相等
互相平分
平行四边形的判定方法
平行
还有其他的判定方法吗?
我们知道平行四边形任意一组对应边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
猜想:一组对边平行且相等的四边形是平行四边形.
已知:如图,四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
分析:先证△ABC≌ △CDA,然后证AD∥BC,再根据“两组对边分别平行的四边形是平行四边形”,得四边形ABCD是平行四边形.
A
D
B
C
猜想验证:一组对边平行且相等的四边形是平行四边形.
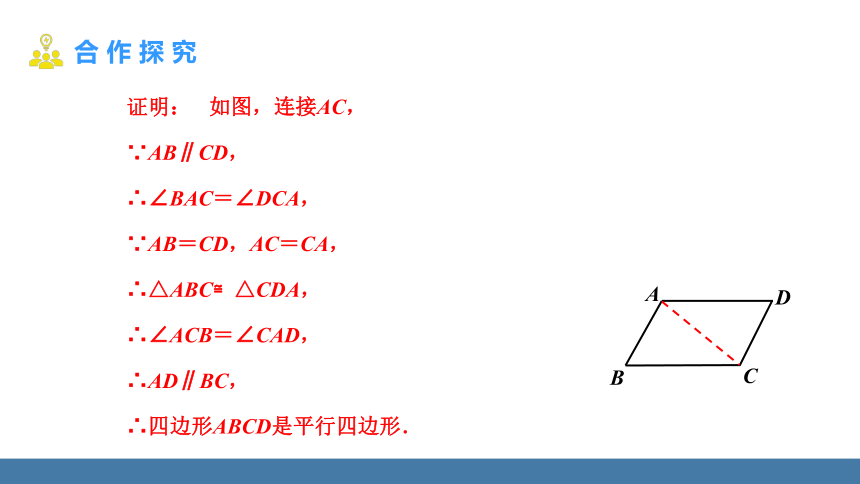
证明:
如图,连接AC,
∵AB∥CD,
∴∠BAC=∠DCA,
∵AB=CD,AC=CA,
∴△ABC≌△CDA,
∴∠ACB=∠CAD,
∴四边形ABCD是平行四边形.
∴AD∥BC,
A
D
B
C
一组对边平行且相等的四边形是平行四边形.
符号语言:
∵AB∥CD,AB=CD(或AD∥BC,AD=BC),
∴四边形ABCD是平行四边形.
A
D
B
C
一组对边平行,另一组对边相等的四边形是平行四边形吗?若是,请说明理由;若不是,请举出反例.
AD∥BC且AB=DC,但四边形ABCD不是平行四边形.
A
B
D
C
不是.
反例:等腰梯形.
例 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点. 求证:四边形EBFD是平行四边形.
A
B
C
D
E
F
证明: ∵四边形ABCD是平行四边形,
∴ AB=CD, AB∥CD,即EB∥FD,
又E,F分别是AB,CD的中点,
∴ EB=FD,
∴四边形EBFD是平行四边形.
1.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A
B
C
D
一组对边平行且相等
两组对边分别平行
∠B+∠A=180°
AD∥BC
B
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥AD
2.如图,在四边形ABCD中,对角线 AC,BD 相交于点 O,OA=OC,BA⊥AC,DC⊥AC.
求证:四边形ABCD是平行四边形.
A
C
D
B
O
分析:根据题意可以得到 AB∥CD,通过证△AOB≌△COD得到 AB=CD即可证得结论.
∵∠BAC=∠DCA,OA=OC,∠AOB=∠COD,
证明:∵ BA⊥AC,DC⊥AC,
∴∠BAC=∠DCA=90°,
∴ △AOB≌△COD,
∴四边形ABCD是平行四边形.
∴ AB∥CD.
∴AB=CD,
A
C
D
B
O
3.如图,在平行四边形ABCD中,E, F分别为边AD, BC的中点,对角线 AC 分别交BE , DF于点G, H.
求证:AG=CH.
A
B
C
D
E
F
G
H
分析:可先证四边形BFDE是平行四边形,
再证△AEG≌△CFH得到AG=CH .
证明: ∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠CFH, ∠EAG=∠FCH.
∵E,F分别为边AD,BC的中点,
∴
∴DE∥BF, DE=BF,
A
B
C
D
E
F
G
H
∴ BE∥DF,
∴四边形BFDE是平行四边形,
∴∠AEG=∠ADF.
∵∠AEG=∠CFH, AE=CF, ∠EAG=∠FCH,
∴ △AEG≌△CFH,
∴ AG=CH.
∴∠AEG=∠CFH.
∵∠ADF=∠CFH,
A
B
C
D
E
F
G
H
平行四边形的判定
判定方法5
符号语言
一组对边平行且相等的四边形是平行四边形
∵ AB∥CD,AB=CD ,
∴四边形ABCD是平行四边形
A
B
C
D
18.1.2.1 平行四边形的判定(2)
1.探索并证明平行四边形的判定方法.
2.能熟练运用平行四边形的判定方法去计算和证明.
1.两组对边分别 的四边形是平行四边形.
2.两组对角分别 的四边形是平行四边形.
3.对角线 的四边形是平行四边形.
4.定义法:两组对边分别______的四边形是平行四边形.
相等
相等
互相平分
平行四边形的判定方法
平行
还有其他的判定方法吗?
我们知道平行四边形任意一组对应边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
猜想:一组对边平行且相等的四边形是平行四边形.
已知:如图,四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
分析:先证△ABC≌ △CDA,然后证AD∥BC,再根据“两组对边分别平行的四边形是平行四边形”,得四边形ABCD是平行四边形.
A
D
B
C
猜想验证:一组对边平行且相等的四边形是平行四边形.
证明:
如图,连接AC,
∵AB∥CD,
∴∠BAC=∠DCA,
∵AB=CD,AC=CA,
∴△ABC≌△CDA,
∴∠ACB=∠CAD,
∴四边形ABCD是平行四边形.
∴AD∥BC,
A
D
B
C
一组对边平行且相等的四边形是平行四边形.
符号语言:
∵AB∥CD,AB=CD(或AD∥BC,AD=BC),
∴四边形ABCD是平行四边形.
A
D
B
C
一组对边平行,另一组对边相等的四边形是平行四边形吗?若是,请说明理由;若不是,请举出反例.
AD∥BC且AB=DC,但四边形ABCD不是平行四边形.
A
B
D
C
不是.
反例:等腰梯形.
例 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点. 求证:四边形EBFD是平行四边形.
A
B
C
D
E
F
证明: ∵四边形ABCD是平行四边形,
∴ AB=CD, AB∥CD,即EB∥FD,
又E,F分别是AB,CD的中点,
∴ EB=FD,
∴四边形EBFD是平行四边形.
1.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A
B
C
D
一组对边平行且相等
两组对边分别平行
∠B+∠A=180°
AD∥BC
B
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥AD
2.如图,在四边形ABCD中,对角线 AC,BD 相交于点 O,OA=OC,BA⊥AC,DC⊥AC.
求证:四边形ABCD是平行四边形.
A
C
D
B
O
分析:根据题意可以得到 AB∥CD,通过证△AOB≌△COD得到 AB=CD即可证得结论.
∵∠BAC=∠DCA,OA=OC,∠AOB=∠COD,
证明:∵ BA⊥AC,DC⊥AC,
∴∠BAC=∠DCA=90°,
∴ △AOB≌△COD,
∴四边形ABCD是平行四边形.
∴ AB∥CD.
∴AB=CD,
A
C
D
B
O
3.如图,在平行四边形ABCD中,E, F分别为边AD, BC的中点,对角线 AC 分别交BE , DF于点G, H.
求证:AG=CH.
A
B
C
D
E
F
G
H
分析:可先证四边形BFDE是平行四边形,
再证△AEG≌△CFH得到AG=CH .
证明: ∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠CFH, ∠EAG=∠FCH.
∵E,F分别为边AD,BC的中点,
∴
∴DE∥BF, DE=BF,
A
B
C
D
E
F
G
H
∴ BE∥DF,
∴四边形BFDE是平行四边形,
∴∠AEG=∠ADF.
∵∠AEG=∠CFH, AE=CF, ∠EAG=∠FCH,
∴ △AEG≌△CFH,
∴ AG=CH.
∴∠AEG=∠CFH.
∵∠ADF=∠CFH,
A
B
C
D
E
F
G
H
平行四边形的判定
判定方法5
符号语言
一组对边平行且相等的四边形是平行四边形
∵ AB∥CD,AB=CD ,
∴四边形ABCD是平行四边形
A
B
C
D
