18.1.2.2 三角形的中位线 课件(共17张PPT)
文档属性
| 名称 | 18.1.2.2 三角形的中位线 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 17:46:32 | ||
图片预览




文档简介
(共17张PPT)
18.1.2.2 三角形的中位线
1.掌握三角形中位线的定义和三角形的中位线定理.
2.能熟练运用三角形的中位线定理.
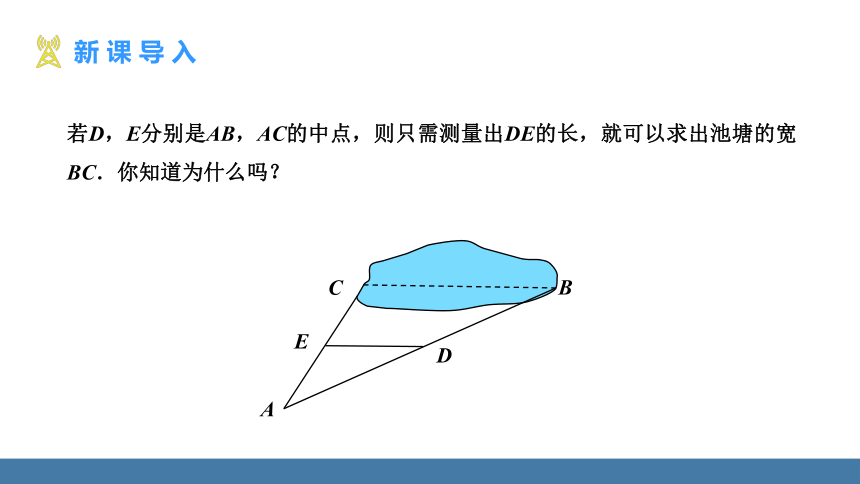
若D,E分别是AB,AC的中点,则只需测量出DE的长,就可以求出池塘的宽BC.你知道为什么吗?
A
E
D
C
B
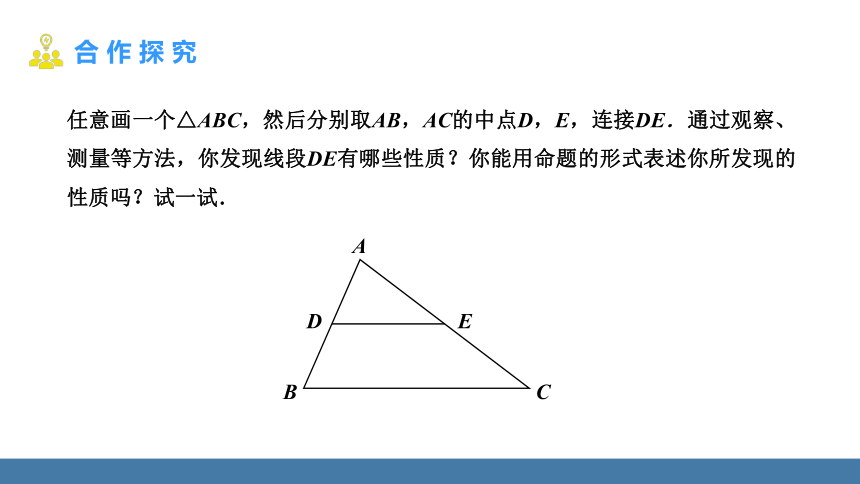
任意画一个△ABC,然后分别取AB,AC的中点D,E,连接DE.通过观察、测量等方法,你发现线段DE有哪些性质?你能用命题的形式表述你所发现的性质吗?试一试.
A
C
B
E
D
A
C
B
E
D
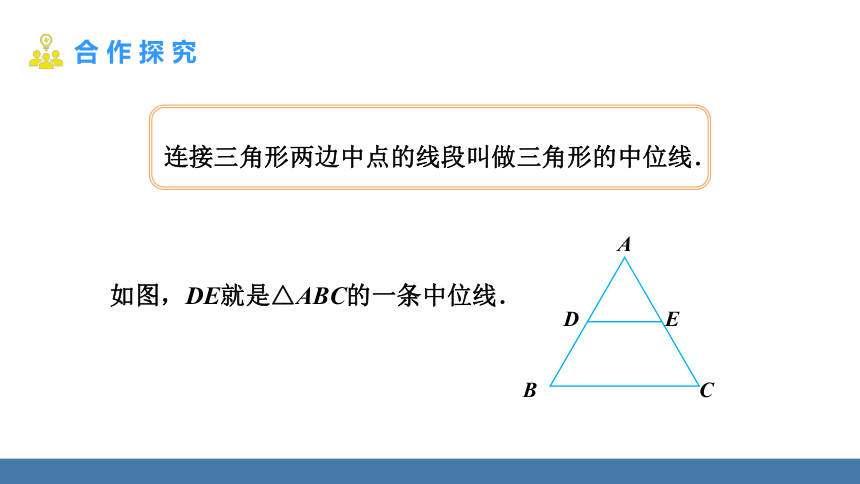
连接三角形两边中点的线段叫做三角形的中位线.
如图,DE就是△ABC的一条中位线.
如图,沿△ABC的中位线DE,DF,EF剪出四个小三角形.将它们叠合在一起,能完全重合吗?
能
中位线DE与BC有怎样的位置关系和数量关系?
DE∥BC且DE= BC
A
E
D
C
B
F
三角形的中位线与第三边有什么关系?
猜想:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
你能证明这个猜想吗?
分析:因为E是AC的中点,可以考虑以点E为中心,把△ADE按顺时针方向旋转180°,得到△CFE,如图.这样就只需证明四边形BCFD是平行四边形.
已知:如图,DE是△ABC的中位线.
求证:DE BC.
//
A
C
B
F
E
D
则D,E,F同在一条直线上,DE=EF,且△ADE≌△CFE.
∴AB∥CF.
又BD=AD=CF,
证明:如图,以点E为旋转中心,把△ADE按顺时针方向旋转180°,得△CFE,
∴∠ADE=∠F,AD=CF,
A
C
B
F
E
D
∴四边形BCFD是平行四边形,
∴DF BC,
//
∴DE BC.
//
三角形的中位线定理
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
符号语言:
∵AD=BD,AE=EC,
∴DE BC.
//
A
C
B
E
D
注意:
(1)理解三角形中位线定义的两层含义:
(2)区分三角形的中位线与中线:
中位线是连接三角形两边中点的线段;
中线是连接一个顶点和它的对边中点的线段.
(3)一个三角形共有三条中位线.
A
C
B
E
D
①如果D,E分别是AB,AC的中点,那么DE是△ABC的中位线;
②如果DE是△ABC的中位线,那么D,E分别是AB,AC的中点.
例1 已知△ABC的面积是S,顺次连接各边中点E,G,F所得的四个三角形面积各是多少?
A
B
C
E
F
G
每个三角形的面积= S
解:根据三角形的中位线定理知,
EF= BC=BG,AE=AB=EB,AF=AC=EG,
故△AEF≌△EBG,
同理,△AEF≌△FGC, △GFE≌ △AEF.
所以,S△AEF =S△EBG =S△FGC =S△GFE=S.
例2 如果△ABC三边的长分别为a,b,c,那么顺次连接各边中点E,G,F所得的四个三角形周长分别是多少?
A
B
C
E
F
G
每个三角形的周长= (a+b+c)
解:根据三角形的中位线定理知,
EF=a,EG= b,GF=c.
故△EGF的周长= a+ b+ c= (a+b+c).
同理,其他三角形的周长也是(a+b+c).
1.如图,D,E分别为△ABC的边AB, AC的中点.则图中是△ABC中位线的是( )
A
B
D
E
C
A
A.线段DE B.线段CD
C.线段BE D.以上都不是
2.如图,已知 E,F 是四边形 ABCD 的对角线 BD 的三等分点,CE,CF 的延长线分别平分 AB,AD.
求证:四边形 ABCD 是平行四边形.
B
A
D
C
E
F
O
G
H
证明:连接AC交BD于点O,连接AE,AF.
∵点G是AB的中点,BE=EF,
∴GE是△ABF的一条中位线,
∴GE∥AF,即CE∥AF,
同理可得 CF∥AE,
∴四边形AFCE是平行四边形,
∴OA=OC,OE=OF.
又BE=DF,
∴OB=OD,
∴四边形ABCD是平行四边形.
B
A
D
C
E
F
O
G
H
三角形中位线
定义
定理
连接三角形两边中点的线段叫做三角形的中位线
三角形的中位线平行于三角形的第三边,并且等于第三边的一半
18.1.2.2 三角形的中位线
1.掌握三角形中位线的定义和三角形的中位线定理.
2.能熟练运用三角形的中位线定理.
若D,E分别是AB,AC的中点,则只需测量出DE的长,就可以求出池塘的宽BC.你知道为什么吗?
A
E
D
C
B
任意画一个△ABC,然后分别取AB,AC的中点D,E,连接DE.通过观察、测量等方法,你发现线段DE有哪些性质?你能用命题的形式表述你所发现的性质吗?试一试.
A
C
B
E
D
A
C
B
E
D
连接三角形两边中点的线段叫做三角形的中位线.
如图,DE就是△ABC的一条中位线.
如图,沿△ABC的中位线DE,DF,EF剪出四个小三角形.将它们叠合在一起,能完全重合吗?
能
中位线DE与BC有怎样的位置关系和数量关系?
DE∥BC且DE= BC
A
E
D
C
B
F
三角形的中位线与第三边有什么关系?
猜想:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
你能证明这个猜想吗?
分析:因为E是AC的中点,可以考虑以点E为中心,把△ADE按顺时针方向旋转180°,得到△CFE,如图.这样就只需证明四边形BCFD是平行四边形.
已知:如图,DE是△ABC的中位线.
求证:DE BC.
//
A
C
B
F
E
D
则D,E,F同在一条直线上,DE=EF,且△ADE≌△CFE.
∴AB∥CF.
又BD=AD=CF,
证明:如图,以点E为旋转中心,把△ADE按顺时针方向旋转180°,得△CFE,
∴∠ADE=∠F,AD=CF,
A
C
B
F
E
D
∴四边形BCFD是平行四边形,
∴DF BC,
//
∴DE BC.
//
三角形的中位线定理
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
符号语言:
∵AD=BD,AE=EC,
∴DE BC.
//
A
C
B
E
D
注意:
(1)理解三角形中位线定义的两层含义:
(2)区分三角形的中位线与中线:
中位线是连接三角形两边中点的线段;
中线是连接一个顶点和它的对边中点的线段.
(3)一个三角形共有三条中位线.
A
C
B
E
D
①如果D,E分别是AB,AC的中点,那么DE是△ABC的中位线;
②如果DE是△ABC的中位线,那么D,E分别是AB,AC的中点.
例1 已知△ABC的面积是S,顺次连接各边中点E,G,F所得的四个三角形面积各是多少?
A
B
C
E
F
G
每个三角形的面积= S
解:根据三角形的中位线定理知,
EF= BC=BG,AE=AB=EB,AF=AC=EG,
故△AEF≌△EBG,
同理,△AEF≌△FGC, △GFE≌ △AEF.
所以,S△AEF =S△EBG =S△FGC =S△GFE=S.
例2 如果△ABC三边的长分别为a,b,c,那么顺次连接各边中点E,G,F所得的四个三角形周长分别是多少?
A
B
C
E
F
G
每个三角形的周长= (a+b+c)
解:根据三角形的中位线定理知,
EF=a,EG= b,GF=c.
故△EGF的周长= a+ b+ c= (a+b+c).
同理,其他三角形的周长也是(a+b+c).
1.如图,D,E分别为△ABC的边AB, AC的中点.则图中是△ABC中位线的是( )
A
B
D
E
C
A
A.线段DE B.线段CD
C.线段BE D.以上都不是
2.如图,已知 E,F 是四边形 ABCD 的对角线 BD 的三等分点,CE,CF 的延长线分别平分 AB,AD.
求证:四边形 ABCD 是平行四边形.
B
A
D
C
E
F
O
G
H
证明:连接AC交BD于点O,连接AE,AF.
∵点G是AB的中点,BE=EF,
∴GE是△ABF的一条中位线,
∴GE∥AF,即CE∥AF,
同理可得 CF∥AE,
∴四边形AFCE是平行四边形,
∴OA=OC,OE=OF.
又BE=DF,
∴OB=OD,
∴四边形ABCD是平行四边形.
B
A
D
C
E
F
O
G
H
三角形中位线
定义
定理
连接三角形两边中点的线段叫做三角形的中位线
三角形的中位线平行于三角形的第三边,并且等于第三边的一半
